Secondary active transporters couple the transport of an ion species down its concentration gradient to the uphill transport of another substrate. Despite the importance of secondary active transport to multidrug resistance, metabolite transport, and nutrient acquisition, among other biological processes, the microscopic steps of the coupling mechanism are not well understood. Often, transport models illustrate coupling mechanisms through a limited number of “major” conformations or states, yet recent studies have indicated that at least some transporters violate these models. The small multidrug resistance transporter EmrE has been shown to couple proton influx to multidrug efflux via a mechanism that incorporates both “major” and “minor” conformational states and transitions. The resulting free exchange transport model includes multiple leak pathways and theoretically allows for both exchange and cotransport of ion and substrate. To better understand how coupled transport can be achieved in such a model, we numerically simulate a free-exchange model of transport to determine the step-by-step requirements for coupled transport. We find that only moderate biasing of rate constants for key transitions produce highly efficient net transport approaching a perfectly coupled, stoichiometric model. We show how a free-exchange model can enable complex phenotypes, including switching transport direction with changing environmental conditions or substrates. This research has broad implications for synthetic biology, as it demonstrates the utility of free-exchange transport models and the fine tuning required for perfectly coupled transport.
Introduction
Secondary active transporters use the energetically favorable flux of one ion down its electrochemical gradient to drive transport of a second substrate in the same (symport) or opposite (antiport) direction. Despite the importance of these integral membrane proteins for nutrient acquisition, metabolite transport, and toxin efflux, the mechanistic details of ion–substrate coupling are still not fully understood (Zhang et al., 2019; Yazaki et al., 2008; Amaral et al., 2014; Silverman, 2002). Frequently, transport mechanisms are depicted by models that include only the minimum number of states and transitions needed to explain transport (Oh and Boudker, 2018; Luo et al., 2018; Lolkema and Slotboom, 2019; Forrest et al., 2011; Quistgaard et al., 2016; Feng et al., 2012; Stein, 1986; Fig. 1). Through restricting transport to a single pathway, these models lead to perfect energetic coupling between substrate and ion. Occasional “slippage,” or transport through pathways apart from those prescribed by perfect coupling, is expected but assumed to be a relatively minor contributor to net flux. Although net transport stoichiometry is challenging to measure accurately, it has been measured via reversal potential for several transporters (Fitzgerald et al., 2017; Kermani et al., 2018; Nguitragool and Miller, 2006), and stoichiometric or near-stoichiometric transport was observed, as expected. Together with crystal structures (Chen et al., 2007; Iancu et al., 2013) that have captured a finite number of states for individual transporters and families, this has led to the widespread representation of such models in the literature.
Stoichiometric models for secondary-active transport. Mechanistic descriptions of transport often depict only the major states and transitions contributing to stochiometric coupled transport of substrate and ion. Here, the transported substrate is represented as a cationic drug (green hexagon), and the driving ion is proton (dark red circle), while the transporter is shown in pale blue. (A) For symport, the transporter binds both drug and proton cooperatively, and alternating access occurs in both this doubly bound state and the apo state. (B) For antiport, drug and proton cannot bind simultaneously, and alternating access occurs only when the transporter is bound to either substrate (drug) or ion (proton).
Stoichiometric models for secondary-active transport. Mechanistic descriptions of transport often depict only the major states and transitions contributing to stochiometric coupled transport of substrate and ion. Here, the transported substrate is represented as a cationic drug (green hexagon), and the driving ion is proton (dark red circle), while the transporter is shown in pale blue. (A) For symport, the transporter binds both drug and proton cooperatively, and alternating access occurs in both this doubly bound state and the apo state. (B) For antiport, drug and proton cannot bind simultaneously, and alternating access occurs only when the transporter is bound to either substrate (drug) or ion (proton).
However, it is becoming clear that deviations from ideal coupled transport may be common for some transporters, and that slippage pathways may even become the dominant transport pathway under certain conditions. For example, GlcPSe, a sugar transporter from Staphylococcus epidermidis, can perform sugar/proton symport, sugar uniport, and proton uniport based on pH conditions, indicating that it is possible for a single protein to engage in both coupled and uncoupled transport pathways (Bazzone et al., 2017). Some transporters engage in multiple transport regimes or stoichiometries based on substrate identity. Examples include Nramp, a metal ion transporter that performs proton-coupled symport of manganese and uniport of cadmium (Bozzi et al., 2019); or the classic sodium–iodide symporter, NIS, that performs 2:1 Na+/I+ symport but also 1:1 perchlorate symport (Dohán et al., 2007). Additionally, single point mutations of LacY result in a variety of leaky phenotypes while still performing net import of sugar molecules (Forrest et al., 2011; Guan and Kaback, 2006; Varela and Wilson, 1996). In these examples, slippage pathways significantly influence net flux. Thus, a mechanistic model that explicitly considers all possibilities for ion-coupled transport is required.
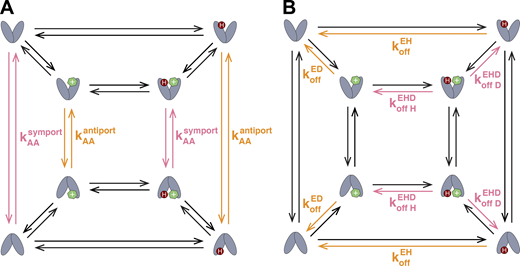
Our laboratory uses EmrE, a proton-coupled multidrug efflux pump from Escherichia coli (Purewal, 1991; Yerushalmi et al., 1995), to investigate the requirements for ion-coupled transport. Since the proton motive force is inwardly directed in E. coli, EmrE confers resistance to toxic polyaromatic cations through proton/drug antiport. EmrE’s small size, stability, and ease of purification make it a model system to study by NMR spectroscopy. This powerful technique can simultaneously provide structural, thermodynamic, and kinetic information, giving unprecedented insight into the transport cycle of an ion-coupled transporter (Robinson et al., 2017; Morrison et al., 2015, 2011; Thomas et al., 2018). Strikingly, NMR reveals that EmrE adopts states and performs transitions nominally “forbidden” for an antiporter: it can both bind drug and proton simultaneously (Robinson et al., 2017) and alternate access in every available state (Gayen et al., 2016; Morrison et al., 2015; Robinson et al., 2017). In light of this evidence, we proposed a “free-exchange” model of transport for EmrE that incorporates all experimentally observed states and transitions (Fig. 2; Robinson et al., 2017). The free-exchange model includes multiple leak pathways, yet WT EmrE demonstrates sufficient coupling to confer resistance to a wide array of toxic compounds in its native E. coli.
The 10-state free-exchange model of EmrE transport. All states and transitions observed for EmrE are incorporated into one unified model. Multiple pathways exist for proton-coupled antiport (2:1 or 1:1 proton/drug stoichiometry), proton-coupled symport, uncoupled drug transport, and uncoupled proton transport (leak). Colors are as in Fig. 1, and states are labeled (apo, E; proton-bound, EH; double-proton-bound, EHH; drug-bound, ED; and proton/drug-bound, EHD). The membrane is not shown for clarity due to the complexity of this model, but the states of the transporter open to either side of the membrane are separated by the orange dotted line and labeled ext (open-out) or int (open-in).
The 10-state free-exchange model of EmrE transport. All states and transitions observed for EmrE are incorporated into one unified model. Multiple pathways exist for proton-coupled antiport (2:1 or 1:1 proton/drug stoichiometry), proton-coupled symport, uncoupled drug transport, and uncoupled proton transport (leak). Colors are as in Fig. 1, and states are labeled (apo, E; proton-bound, EH; double-proton-bound, EHH; drug-bound, ED; and proton/drug-bound, EHD). The membrane is not shown for clarity due to the complexity of this model, but the states of the transporter open to either side of the membrane are separated by the orange dotted line and labeled ext (open-out) or int (open-in).
Here, we investigate the requirements for coupled transport using mass action kinetics to simulate the free-exchange model of transport (Horn and Jackson, 1972). Using a bottom-up approach, we first model the simplest implementation of free exchange, the 8-state model (Eq. 1; Fig. 3), before investigating the 10-state model (Eq. 2; Fig. 2) needed to describe EmrE transport (Robinson et al., 2017). We base our simulations on EmrE because it is one of the few secondary active transporters for which the rate constants are experimentally measured or estimated for all of the microscopic steps in the transport cycle. We demonstrate that only modest biasing of rates is necessary to achieve reasonably well-coupled transport, a result that has broad implications both for synthetic biology and for our understanding of the fundamental nature of active transport.
The 8-state free-exchange model of generalized transport. The transporter can assume four different binding states (apo, E; proton-bound, EH; drug-bound, ED; and proton/drug-bound, EHD). All states can perform alternating access. The pathways leading to antiport or symport are shown in B and C, respectively. In either case, proton and drug can bind in any order. However, different pairs of key states must alternate access to achieve coupled antiport (ED and EH) or coupled symport (E and EHD). Colors and labeling are as in Figs. 1 and 2.
The 8-state free-exchange model of generalized transport. The transporter can assume four different binding states (apo, E; proton-bound, EH; drug-bound, ED; and proton/drug-bound, EHD). All states can perform alternating access. The pathways leading to antiport or symport are shown in B and C, respectively. In either case, proton and drug can bind in any order. However, different pairs of key states must alternate access to achieve coupled antiport (ED and EH) or coupled symport (E and EHD). Colors and labeling are as in Figs. 1 and 2.
Materials and methods
Numerical simulations of transport
Simulated liposomal flux assay. Simulations are conducted as virtual liposomal flux assays. The simulation begins with a 10-fold proton gradient and identical drug concentration inside and outside the proteoliposome. We assume infinite buffering capacity, so the proton gradient, represented as Hr, remains constant throughout the simulation. Unless otherwise indicated, Hr is set at 10. The simulation is then run until the drug concentration reaches steady state. Transport outcome is assessed by Tr, or the ratio of internal to external drug concentration at steady state (Tr = [Drug]int/[Drug]ext).
Simulated liposomal flux assay. Simulations are conducted as virtual liposomal flux assays. The simulation begins with a 10-fold proton gradient and identical drug concentration inside and outside the proteoliposome. We assume infinite buffering capacity, so the proton gradient, represented as Hr, remains constant throughout the simulation. Unless otherwise indicated, Hr is set at 10. The simulation is then run until the drug concentration reaches steady state. Transport outcome is assessed by Tr, or the ratio of internal to external drug concentration at steady state (Tr = [Drug]int/[Drug]ext).
Rate constant definitions for the free-exchange model simulations
| Parameter (unit) . | Transition . | Side of membrane . | Process . | Physiological value/range . |
|---|---|---|---|---|
| k1 (M−1 s−1) | Eext → EHext | External | Proton-ona | 1 × 1010 |
| k2 (s−1) | Eext ← EHext | External | Proton-off | 1–1,000,000 |
| k3 (M−1 s−1) | Eint → EHint | Internal | Proton-ona | 1 × 1010 |
| k4 (s−1) | Eint ← EHint | Internal | Proton-off | 1–1,000,000 |
| k5 (M−1 s−1) | EDext → EHDext | External | Proton-ona | 1 × 1010 |
| k6 (s−1) | EDext ← EHDext | External | Proton-off | 1–1,000,000 |
| k7 (M−1 s−1) | EDint → EHDint | Internal | Proton-ona | 1 × 1010 |
| k8 (s−1) | EDint ← EHDint | Internal | Proton-off | 0.01–10,000 |
| k9 (M−1 s−1) | Eext → EDext | External | Drug-onb | 1 × 107 |
| k10 (s−1) | Eext ← EDext | External | Drug-off | 0.01–10,000 |
| k11 (M−1 s−1) | Eint → EDint | Internal | Drug-onb | 1 × 107 |
| k12 (s−1) | Eint ← EDint | Internal | Drug-off | 0.01–10,000 |
| k13 (M−1 s−1) | EHext → EHDext | External | Drug-onb | 1 × 107 |
| k14 (s−1) | EHext ← EHDext | External | Drug-off | 0.01–10,000 |
| k15 (M−1 s−1) | EHint → EHDint | Internal | Drug-onb | 1 × 107 |
| k16 (s−1) | EHint ← EHDint | Internal | Drug-off | 0.01–10,000 |
| k17 (s−1) | EHint → EHext | Alternating access | 1–100 | |
| k18 (s−1) | EHint ← EHext | Alternating access | 1–100 | |
| k19 (s−1) | Eint → Eext | Alternating access | 1–100 | |
| k20 (s−1) | Eint ← Eext | Alternating access | 1–100 | |
| k21 (s−1) | EDint → EDext | Alternating access | 1–100 | |
| k22 (s−1) | EDint ← EDext | Alternating access | 1–100 | |
| k23 (s−1) | EHDint → EHDext | Alternating access | 1–100 | |
| k24 (s−1)c | EHDint ← EHDext | Alternating access | 1–100 | |
| k25 (s−1)c | EHHint → EHHext | Alternating access | 1–100 | |
| k26 (s−1)c | EHHint ← EHHext | Alternating access | 1–100 | |
| k27 (M−1 s−1)c | EHext → EHHext | External | Proton-ona | 1 × 1010 |
| k28 (s−1)c | EHext ← EHHext | External | Proton-off | 1–1,000,000 |
| k29 (M−1 s−1)c | EHint → EHHint | Internal | Proton-ona | 1 × 1010 |
| k30 (s−1)c | EHint ← EHHint | Internal | Proton-off | 1–1,000,000 |
| Parameter (unit) . | Transition . | Side of membrane . | Process . | Physiological value/range . |
|---|---|---|---|---|
| k1 (M−1 s−1) | Eext → EHext | External | Proton-ona | 1 × 1010 |
| k2 (s−1) | Eext ← EHext | External | Proton-off | 1–1,000,000 |
| k3 (M−1 s−1) | Eint → EHint | Internal | Proton-ona | 1 × 1010 |
| k4 (s−1) | Eint ← EHint | Internal | Proton-off | 1–1,000,000 |
| k5 (M−1 s−1) | EDext → EHDext | External | Proton-ona | 1 × 1010 |
| k6 (s−1) | EDext ← EHDext | External | Proton-off | 1–1,000,000 |
| k7 (M−1 s−1) | EDint → EHDint | Internal | Proton-ona | 1 × 1010 |
| k8 (s−1) | EDint ← EHDint | Internal | Proton-off | 0.01–10,000 |
| k9 (M−1 s−1) | Eext → EDext | External | Drug-onb | 1 × 107 |
| k10 (s−1) | Eext ← EDext | External | Drug-off | 0.01–10,000 |
| k11 (M−1 s−1) | Eint → EDint | Internal | Drug-onb | 1 × 107 |
| k12 (s−1) | Eint ← EDint | Internal | Drug-off | 0.01–10,000 |
| k13 (M−1 s−1) | EHext → EHDext | External | Drug-onb | 1 × 107 |
| k14 (s−1) | EHext ← EHDext | External | Drug-off | 0.01–10,000 |
| k15 (M−1 s−1) | EHint → EHDint | Internal | Drug-onb | 1 × 107 |
| k16 (s−1) | EHint ← EHDint | Internal | Drug-off | 0.01–10,000 |
| k17 (s−1) | EHint → EHext | Alternating access | 1–100 | |
| k18 (s−1) | EHint ← EHext | Alternating access | 1–100 | |
| k19 (s−1) | Eint → Eext | Alternating access | 1–100 | |
| k20 (s−1) | Eint ← Eext | Alternating access | 1–100 | |
| k21 (s−1) | EDint → EDext | Alternating access | 1–100 | |
| k22 (s−1) | EDint ← EDext | Alternating access | 1–100 | |
| k23 (s−1) | EHDint → EHDext | Alternating access | 1–100 | |
| k24 (s−1)c | EHDint ← EHDext | Alternating access | 1–100 | |
| k25 (s−1)c | EHHint → EHHext | Alternating access | 1–100 | |
| k26 (s−1)c | EHHint ← EHHext | Alternating access | 1–100 | |
| k27 (M−1 s−1)c | EHext → EHHext | External | Proton-ona | 1 × 1010 |
| k28 (s−1)c | EHext ← EHHext | External | Proton-off | 1–1,000,000 |
| k29 (M−1 s−1)c | EHint → EHHint | Internal | Proton-ona | 1 × 1010 |
| k30 (s−1)c | EHint ← EHHint | Internal | Proton-off | 1–1,000,000 |
Proton on-rates are assumed to be diffusion-limited and constant as observed for EmrE (Adam et al., 2007).
Drug on-rates are assumed to be diffusion-limited and slower than proton on-rates as observed for EmrE (Robinson et al., 2017; Adam et al., 2007).
Only used in 10-state model.
Initial conditions for simulations of liposomal-flux assays
| Parameter (unit) . | Meaning . | Estimated values . |
|---|---|---|
| Hint (M) | Interior [H] (constant) | 10−6.5 (pH = 6.5) |
| Hext (M) | Exterior [H] (constant) | 10−7.5 (pH = 7.5) |
| Dint (M) | Initial internal [drug] | 25 × 10−9 |
| Dext (M) | Initial external [drug] | 25 × 10−9 |
| Parameter (unit) . | Meaning . | Estimated values . |
|---|---|---|
| Hint (M) | Interior [H] (constant) | 10−6.5 (pH = 6.5) |
| Hext (M) | Exterior [H] (constant) | 10−7.5 (pH = 7.5) |
| Dint (M) | Initial internal [drug] | 25 × 10−9 |
| Dext (M) | Initial external [drug] | 25 × 10−9 |
Due to the fully reversible system, initial conditions of EmrE species do not impact final steady-state drug concentration (Tr; Craciun and Feinberg, 2006).
Rate constants used in each experiment.
| . | Independent and combined effects of alternating-access rates and substrate off-rates on transport outcome . | Simulating the 10-state model . | Understanding the effects of ΔpH on Transport in the 8- and 10-state models . | Understanding how drug-induced rate constants may drive antiport vs. symport . | ||||
|---|---|---|---|---|---|---|---|---|
| Parameter (Unit) . | Fig. 7 A . | Fig. 7 B . | Fig. 7 C . | Fig. 8 . | Fig. 9 (8-state) . | Fig. 9 (10-state) . | Fig. 10 A . | Fig. 10 B . |
| k1 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 |
| k2 (s−1) | 1,000 | 1–1,000,000 | 1–1,000,000 | 1–1,000,000 | 63.1 | 63.1 | 63.1 | 1,000 |
| k3 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 |
| k4 (s−1) | 1,000 | 1–1,000,000 | 1–1,000,000 | 1–1,000,000 | 63.1 | 63.1 | 63.1 | 1,000 |
| k5 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 |
| k6 (s−1) | 1,000 | 1–1,000,000 | 1–1,000,000 | 1–1,000,000 | 1,584 | 1584 | 6.3 × 10−5–6.3 × 107a | 0.001–1 × 109* |
| k7 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 |
| k8 (s−1) | 1,000 | 0.01–10,000 | 0.01–10,000 | 0.01–10,000 | 1,584 | 1584 | 6.3 × 10−5–6.3 × 107a | 0.001–1 × 109* |
| k9 (M−1 s−1) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| k10 (s−1) | 1 | 0.01–10,000 | 0.01–10,000 | 0.01–10,000 | 0.631 | 0.631 | 0.01–10,000 | 0.01–10,000 |
| k11 (M−1 s−1) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| k12 (s−1) | 1 | 0.01–10,000 | 0.01–10,000 | 0.01–10,000 | 0.631 | 0.631 | 0.01–10,000 | 0.01–10,000 |
| k13 (M−1 s−1) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| k14 (s−1) | 1 | 0.01–10,000 | 0.01–10,000 | 0.01–10,000 | 10 | 10 | 0.01–10,000 | 0.01–10,000 |
| k15 (M−1 s−1) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| k16 (s−1) | 1 | 0.01–10,000 | 0.01–10,000 | 0.01–10,000 | 10 | 10 | 0.01–10,000 | 0.01–10,000 |
| k17 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 100 | 100 | 100 | 100 |
| k18 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 100 | 100 | 100 | 100 |
| k19 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 40 | 40 | 40 | 40 |
| k20 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 40 | 40 | 40 | 40 |
| k21 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 7.3 | 7.3 | 1–100 | 1–100 |
| k22 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 7.3 | 7.3 | 1–100 | 1–100 |
| k23 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 8.9 | 8.9 | 1–100 | 1–100 |
| k24 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 8.9 | 8.9 | 1–100 | 1–100 |
| k25 (s−1) | 1 | 220 | 220 | 220 | ||||
| k26 (s−1) | 1 | 220 | 220 | 220 | ||||
| k27 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | ||||
| k28 (s−1) | 10, 100, 316.2, 1,000, 100,000, 1,000,000 | 1,000 | 1,000 | 100,000 | ||||
| k29 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | ||||
| k30 (s−1) | 10, 100, 316.2, 1,000, 100,000, 1,000,000 | 1,000 | 1,000 | 100,000 | ||||
| . | Independent and combined effects of alternating-access rates and substrate off-rates on transport outcome . | Simulating the 10-state model . | Understanding the effects of ΔpH on Transport in the 8- and 10-state models . | Understanding how drug-induced rate constants may drive antiport vs. symport . | ||||
|---|---|---|---|---|---|---|---|---|
| Parameter (Unit) . | Fig. 7 A . | Fig. 7 B . | Fig. 7 C . | Fig. 8 . | Fig. 9 (8-state) . | Fig. 9 (10-state) . | Fig. 10 A . | Fig. 10 B . |
| k1 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 |
| k2 (s−1) | 1,000 | 1–1,000,000 | 1–1,000,000 | 1–1,000,000 | 63.1 | 63.1 | 63.1 | 1,000 |
| k3 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 |
| k4 (s−1) | 1,000 | 1–1,000,000 | 1–1,000,000 | 1–1,000,000 | 63.1 | 63.1 | 63.1 | 1,000 |
| k5 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 |
| k6 (s−1) | 1,000 | 1–1,000,000 | 1–1,000,000 | 1–1,000,000 | 1,584 | 1584 | 6.3 × 10−5–6.3 × 107a | 0.001–1 × 109* |
| k7 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 |
| k8 (s−1) | 1,000 | 0.01–10,000 | 0.01–10,000 | 0.01–10,000 | 1,584 | 1584 | 6.3 × 10−5–6.3 × 107a | 0.001–1 × 109* |
| k9 (M−1 s−1) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| k10 (s−1) | 1 | 0.01–10,000 | 0.01–10,000 | 0.01–10,000 | 0.631 | 0.631 | 0.01–10,000 | 0.01–10,000 |
| k11 (M−1 s−1) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| k12 (s−1) | 1 | 0.01–10,000 | 0.01–10,000 | 0.01–10,000 | 0.631 | 0.631 | 0.01–10,000 | 0.01–10,000 |
| k13 (M−1 s−1) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| k14 (s−1) | 1 | 0.01–10,000 | 0.01–10,000 | 0.01–10,000 | 10 | 10 | 0.01–10,000 | 0.01–10,000 |
| k15 (M−1 s−1) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| k16 (s−1) | 1 | 0.01–10,000 | 0.01–10,000 | 0.01–10,000 | 10 | 10 | 0.01–10,000 | 0.01–10,000 |
| k17 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 100 | 100 | 100 | 100 |
| k18 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 100 | 100 | 100 | 100 |
| k19 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 40 | 40 | 40 | 40 |
| k20 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 40 | 40 | 40 | 40 |
| k21 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 7.3 | 7.3 | 1–100 | 1–100 |
| k22 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 7.3 | 7.3 | 1–100 | 1–100 |
| k23 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 8.9 | 8.9 | 1–100 | 1–100 |
| k24 (s−1) | 1–100 | 1, 10, 100 | 1, 2, 3, 4, 5 | 1 | 8.9 | 8.9 | 1–100 | 1–100 |
| k25 (s−1) | 1 | 220 | 220 | 220 | ||||
| k26 (s−1) | 1 | 220 | 220 | 220 | ||||
| k27 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | ||||
| k28 (s−1) | 10, 100, 316.2, 1,000, 100,000, 1,000,000 | 1,000 | 1,000 | 100,000 | ||||
| k29 (M−1 s−1) | 1 × 1010 | 1 × 1010 | 1 × 1010 | 1 × 1010 | ||||
| k30 (s−1) | 10, 100, 316.2, 1,000, 100,000, 1,000,000 | 1,000 | 1,000 | 100,000 | ||||
This number is solved to complete the thermodynamic cycle. These pKa values range from 1 to 14.2.
Constraints and simplifying assumptions
In buffered drug-monitored liposomal transport assays (Robinson et al., 2018) and in live cells (Bakker and Mangerich, 1981), the proton motive force remains relatively constant. Therefore, we make the simplifying assumption of infinite buffering, such that internal/external proton concentration remains constant throughout the simulation.
The model is also simplified by thermodynamic principles and assumptions we make based on experimental data for EmrE. In the 8-state (Fig. 3) and 10-state (Fig. 2) models, there are a total of 24 and 30 rate constants, respectively (Table 3). The thermodynamic cycle constrains drug and proton binding (pKa1 + pKd2 = pKd1 + pKaD), reducing the number of independent rate constants, where pKa = −log(Ka) and pKd = −log(Kd), with the relevant equilibria illustrated in Fig. 5.
We imposed three additional constraints based on experimental observations for EmrE: (1) rate constants for substrate-on and proton-on are diffusion limited and uniformly constant (Fig. 5 A; Morrison et al., 2015; Adam et al., 2007); (2) all on- and off-rate constants are identical for open-in and open-out conformations, which is true for EmrE due to its unique antiparallel topology and identical open-in and open-out structures (Fig. 5 B; Morrison et al., 2011); and (3) rate constants for alternating access are equal for open-in to open-out and open-out to open-in conformations (Fig. 5 C; Morrison et al., 2015, 2011; Gayen et al., 2016). It is important to note that these rate constants were all measured for EmrE in the absence of any proton gradient or transmembrane voltage, and the last two constraints may not reflect the behavior of EmrE in the presence of transmembrane gradients. Altogether, these thermodynamic and EmrE-based constraints reduce the total free parameters to 8 for the 8-state model and 10 for the 10-state model, simplifying this initial exploration of the free exchange model.
Constraints used in modeling transport. These constraints are based on experimental observations for EmrE. (A) Both drug- and proton-on rates are diffusion-limited and constant. (B) Binding affinities are the same for open-in and open-out conformations of the transporter. Additionally, these four values are constrained by the thermodynamic cycle (). (C) All alternating access rates are equal going in either direction. Colors are as in Figs. 1, 2, and 3.
Constraints used in modeling transport. These constraints are based on experimental observations for EmrE. (A) Both drug- and proton-on rates are diffusion-limited and constant. (B) Binding affinities are the same for open-in and open-out conformations of the transporter. Additionally, these four values are constrained by the thermodynamic cycle (). (C) All alternating access rates are equal going in either direction. Colors are as in Figs. 1, 2, and 3.
Investigating the requirements for coupled symport and antiport in the 8-state model
Certain key transitions predict dominance of transport phenotype. Free exchange includes all possible transport pathways in one model. To tip the balance of transport toward a single type of proton-coupled transport, rate constants need to favor one pathway over the others. (A) Alternating access rates directly influence coupling if the key transitions for antiport or symport pathways are faster. (B) Substrate off-rates indirectly influence transport by altering the partitioning between futile binding/release on one side of the membrane and productive transport of molecules through key alternating access transitions. Colors are as in Figs. 1, 2, 3, and 5.
Certain key transitions predict dominance of transport phenotype. Free exchange includes all possible transport pathways in one model. To tip the balance of transport toward a single type of proton-coupled transport, rate constants need to favor one pathway over the others. (A) Alternating access rates directly influence coupling if the key transitions for antiport or symport pathways are faster. (B) Substrate off-rates indirectly influence transport by altering the partitioning between futile binding/release on one side of the membrane and productive transport of molecules through key alternating access transitions. Colors are as in Figs. 1, 2, 3, and 5.
Finally, to test whether off-rate constants and alternating-access rate constants were additive or synergistic, we varied both Roff and RAA (Table 3, column 3). Alternating-access rate constants were set at 1, 2, 3, 4, or 5 s−1 to span 0.125 ≤ RAA ≤ 5.
Modeling the effect of a second protonation event
The liposomal assay simulations were repeated using the 10-state model, which includes a second protonation event. Since protonation is sequential, this model includes an additional constraint that the first proton binds with higher affinity than the second proton, pKa1 ≥ pKa2. This negative linkage between two proton binding events is expected for two protonation sites in close proximity within a hydrophobic environment, as observed for EmrE (Morrison et al., 2015). We again varied substrate-off rate constants, with simulations performed for six values of pKa2 (Table 3, column 4). All alternating-access rate constants were held constant at 1 s−1.
Investigating influence of environmental pH on transport
Our initial simulations all used an inverted-physiological pH parameter with lower pH on the inside of the membrane to mimic our liposomal flux assays (Robinson et al., 2017). However, to explore how pH affects transport under conditions more closely aligned to the environment of a transporter in the bacterial inner membrane, we performed additional simulations holding pHint = 7.4 while varying pHext ±2 units (pHext = 5.4–9.4). This was tested in both the 8-state model and 10-state model to see if the extent of drug transport drug differed depending on the number of proton binding events. For the 8-state model, we used an antiport configuration with RAA = 10 and Roff = 0.1 (Table 3, column 5); for the 10-state model, we used rates estimated for EmrE interacting with the substrate tetraphenyl phosphonium+ (Table 3, column 6; Robinson et al., 2017).
Investigating how a single transporter can act as both an antiporter and a symporter
For these simulations, we varied the drug-dependent rate constants while holding constant the protein-specific rate constants. Rate constants that vary with the identity of the transported drug include drug-off (, ), proton-off for the drug-bound state (), and alternating-access rate constants in the ED and EHD states (kAAED, kAAEHD). Protein-specific variables are invariant to drug identity and include alternating-access rate constant in the apo, singly, and doubly protonated states (kAAE, kAAEH, kAAEH) as well as proton-off rate constants (koffEH and koffEHH, which dictate pKa1 and pKa2, respectively). We ran simulations scanning through physiological ranges for koffED, koffEHD, kAAED, and kAAEHD for two different pKa combinations: pKa1 = 8.2 and pKa2 = 7.0, representing WT EmrE (Table 3, column 7), and pKa1 = 7.0 and pKa2 = 5.0, representing a mutant with pKa values downshifted toward more typical glutamate pKa values (Table 3, column 8). Tr was used to assess whether the downshifted mutant permitted both antiport and symport upon changes to drug-dependent rates. These experiments followed pH conditions for liposomal transport assays.
Results
Building mass-action kinetic models of free exchange
Our 8-state model includes all states required to describe both coupled antiport and coupled symport of one proton and one drug (Fig. 3, B and C), while our 10-state model includes the experimentally observed states required to describe two-proton–coupled transport by EmrE (Fig. 2). Both models contain three types of rate constants that determine net transport phenotype: substrate-on rate constants, substrate-off rate constants, and alternating-access rate constants. These are constrained three different ways based on observations of EmrE. First, we assume that (1) substrate on-rates are diffusion-limited (Adam et al., 2007; Fig. 5 A). For EmrE, all drug substrates studied in detail have similar on-rates, and the off-rate determines each binding affinity, which ranges over five orders of magnitude (Adam et al., 2007; Morrison and Henzler-Wildman, 2014). Similarly, we assume that proton on-rate is uniformly constant and diffusion limited, and off-rate determines pKa (Morrison et al., 2015; Adam et al., 2007). Next, since EmrE has an antiparallel topology that results in identical open-in and open-out conformations (Morrison et al., 2015), we assume that (2) binding affinities (and thus on- and off-rates) are identical for open-in and open-out states (Fig. 5 B) and that (3) alternating-access rates are equal in both directions (Fig. 5 C; Morrison et al., 2015, 2011; Gayen et al., 2016). As a result, substrate-off rate constants and alternating-access rate constants are the two groups of rate constants that are variable parameters in our simulations.
Requirements for highly coupled transport of one H+ and one substrate
Fig. 3 depicts the antiport and symport pathways within the 8-state model. While multiple pathways exist for both modes of transport, each contain key transitions that couple proton and drug flux across the membrane: alternating access in the EH and ED states for antiport or the E and EHD states for symport. For a complete cycle of antiport, EH must alternate access to translocate bound proton in one direction, while ED must alternate access to translocate drug in the opposite direction. Similarly, a complete cycle of symport requires alternating access of EHD to simultaneously translocate bound drug and proton in one direction before alternating access of E returns the empty transporter to the opposite side. These are exactly the states where alternating access occurs in the single-pathway, tightly coupled transport models shown in Fig. 1.
If all rate constants in the free exchange model are equal, all pathways are equally likely, and the transporter simply facilitates downhill diffusion of both proton and drug. To achieve coupled transport, rate constants must be skewed to tip the balance between transport regimes by increasing the relative flux through the key transitions for antiport or symport. We hypothesized that this could be accomplished through manipulating the rates for substrate-off and/or alternating access. Varying the alternating-access rate constants will directly impact the relative frequency of these transitions that are critical for moving substrate across the membrane. On the other hand, varying substrate off-rate constants alters the partitioning between futile substrate binding and release and productive movement of molecules across the membrane via the key alternating-access transitions. We explored the independent and combined effects of substrate off-rates and alternating-access rate through three experiments to explore the transport behavior of the free-exchange model.
In the first set of simulations, alternating-access rate constants were varied around a physiological range while holding proton off-rate constants at 1,000 s−1 and drug off-rates constants at 1 s−1 for all states of the transporter (Table 3, column 1). Alternating-access rate constants were grouped according their contribution to antiport or symport and covaried to reduce the number of free variables within the model. We examined how shifting the ratio RAA (Eq. 4) of the key alternating-access rate constants (Eqs. 5 and 6) affected Tr. For values of RAA > 1, the key antiport states alternate access faster, while for RAA < 1, this is true for the key symport states. Fig. 7 A shows the relationship between RAA and Tr. To reach the 80% benchmark for highly coupled transport, the alternating-access rates need to be skewed 25-fold in either direction: RAA ≥ 25 for antiport or RAA ≤ 1/25 for symport. This reveals the expected symmetry within the 8-state free-exchange model: whatever degree of biasing is required for highly coupled antiport is the inverse of what is required for highly coupled symport.
Rate bias is sufficient to achieve coupled transport in the 8-state model. Four sets of simulations explore the independent and combined effects of substrate off-rates and alternating access rates on drug gradient (Tr) observed at steady state with a driving force ΔpH = 1. In the 8-state model, perfectly coupled transport will result in a 10-fold drug gradient at steady state: Tr = 10 in the case of antiport and Tr = 0.1 in the case of symport. The orange dashed line represents 80% of the maximum coupling efficiency for antiport; the pink dashed line represents 80% of the maximum coupling efficiency for symport. (A) When only alternating access rates are varied, skewing the relative rates of alternating access in the states critical for symport or antiport pathways by 25-fold (RAA = 25 for antiport and 1/25 for symport) achieves ∼80% of the maximum coupling efficiency. RAA is defined in Eq. 4. (B) When only substrate off-rates are varied, skewing the relative substrate off-rates for symport- and antiport-critical states by 630-fold (Roff = 630 for symport, 1/630 for antiport) is needed to achieve ∼80% of the maximum coupling efficiency if the alternating access rates are sufficiently slow (kAA ≤ 1 s−1, blue line). If the uniformly constant alternating access rates are faster than ∼10 s−1 (orange, yellow, and purple lines), transport is less efficient and the antiport/symport phenotypes diverge in behavior. Roff is defined in Eq. 7. (C) Steady-state transport phenotypes are independent of drug concentration, regardless of alternating access rate. Lines for drug concentrations ranging from 1 nM to 50 mM lie on top of each other. (D) When both Roff and RAA are varied simultaneously, less skewing of the relative rates is needed to achieve highly coupled transport. The colored lines reflect the effect of varying Roff at different values of RAA (RAA = 0.2, blue; 0.5, orange; 1.0, yellow; 2.0, purple; 5.0, green). For all simulations, kAA = 1 s−1. With RAA = 5.0 favoring antiport (green), 80% of the maximum coupling efficiency is achieved with a ratio of off-rates of only Roff = 1/23.
Rate bias is sufficient to achieve coupled transport in the 8-state model. Four sets of simulations explore the independent and combined effects of substrate off-rates and alternating access rates on drug gradient (Tr) observed at steady state with a driving force ΔpH = 1. In the 8-state model, perfectly coupled transport will result in a 10-fold drug gradient at steady state: Tr = 10 in the case of antiport and Tr = 0.1 in the case of symport. The orange dashed line represents 80% of the maximum coupling efficiency for antiport; the pink dashed line represents 80% of the maximum coupling efficiency for symport. (A) When only alternating access rates are varied, skewing the relative rates of alternating access in the states critical for symport or antiport pathways by 25-fold (RAA = 25 for antiport and 1/25 for symport) achieves ∼80% of the maximum coupling efficiency. RAA is defined in Eq. 4. (B) When only substrate off-rates are varied, skewing the relative substrate off-rates for symport- and antiport-critical states by 630-fold (Roff = 630 for symport, 1/630 for antiport) is needed to achieve ∼80% of the maximum coupling efficiency if the alternating access rates are sufficiently slow (kAA ≤ 1 s−1, blue line). If the uniformly constant alternating access rates are faster than ∼10 s−1 (orange, yellow, and purple lines), transport is less efficient and the antiport/symport phenotypes diverge in behavior. Roff is defined in Eq. 7. (C) Steady-state transport phenotypes are independent of drug concentration, regardless of alternating access rate. Lines for drug concentrations ranging from 1 nM to 50 mM lie on top of each other. (D) When both Roff and RAA are varied simultaneously, less skewing of the relative rates is needed to achieve highly coupled transport. The colored lines reflect the effect of varying Roff at different values of RAA (RAA = 0.2, blue; 0.5, orange; 1.0, yellow; 2.0, purple; 5.0, green). For all simulations, kAA = 1 s−1. With RAA = 5.0 favoring antiport (green), 80% of the maximum coupling efficiency is achieved with a ratio of off-rates of only Roff = 1/23.
In the third set of simulations, we varied both Roff and RAA. Fig. 7 D shows Tr as a function of Roff similar to the second set of simulations; however, each curve now represents a different RAA value (Table 3, column 3). With fivefold skewing of alternating-access rate constants (Fig. 7 D, green line), only a 23-fold difference in the substrate off-rate constants is needed to achieve 80% , much less than the 630-fold-difference required if alternating-access rates are uniformly held at 1 s−1 (Fig. 7 B). This result demonstrates that the combined effects of alternating-access and substrate off-rates synergize nonlinearly such that robust proton-coupled transport phenotypes can be achieved without the need for highly skewed rates. In other words, highly coupled transport does not require states or pathways to be excluded from the transport model. Only relatively modest biasing of rate constants channels the majority of flux through key pathways and achieves relatively well-coupled transport.
Modeling the transport cycle of EmrE
EmrE requires a more complex transport mechanism due to its ability to perform two-proton coupled antiport (Fig. 2). Since there is no evidence that EmrE can simultaneously transport drug and two protons, the 10-state model introduces an asymmetry. Whereas the 8-state model possesses a maximum of 1 coupled proton per drug (n = 1, Eq. 8) for both antiport and symport, the 10-state model increases n for antiport to n = 2, while symport remains at n = 1. In other words, an initial 1.0 pH unit gradient can now drive a maximum 100-fold drug gradient (Tr = 100) via antiport but can still only drive a maximum 10-fold drug (Tr = 1/10) gradient via symport. In effect, this extra protonation event creates a new key antiport state, EHH (EmrE bound to two protons, see Fig. 2), that cannot contribute to symport. We explored how this asymmetry affects the distribution of transport outcomes.
Since the second protonation event introduces an additional proton off-rate (koffEHH), we repeated the experiment varying Roff (Fig. 7 B, blue trace) but over six different values of this newly introduced proton off-rate (Fig. 8). Proton on-rates are assumed to be diffusion limited and constant at 1010 s−1, so this is recapitulated as six curves of different pKa2 values for the second protonation event (Table 3, column 4). Protonation appears to be sequential in EmrE, thus requiring pKa1 ≥ pKa2 (Morrison et al., 2015). This restricts the parameter space, resulting in the gray portion of Fig. 8 (for example, if pKa2 = 9, pKa1 can range only from 9 to 10). At low pKa2 values, the second protonation event is rare, and the 10-state model greatly resembles the 8-state model (Fig. 8, overlapping orange and blue lines). However, as the value of pKa2 rises above 7, the EHH state becomes populated, and transitions through this state contribute to net flux, resulting in increasing domination of antiport phenotypes. In fact, as pKa2 approaches 9, the system starts to resemble a stoichiometric transport model, where perfect competition yields perfectly coupled antiport. Thus, the second protonation event biases the transporter toward antiport under these particular conditions with only ΔpH and no membrane potential.
The 10-state model is biased toward antiport when driven solely by a pH gradient. We varied the second protonation value, pKa2, to examine how this parameter affects transport in the 10-state model. Here, pKa2 = 4, blue; 5, orange (overlapped with blue); 7, yellow; 7.5, purple; 8, green; and 9, cyan. Unlike the 8-state model, where inverting the rates for an efficient antiporter can produce an equally efficient symporter, the 10-state model is asymmetric. The requirement that EmrE sequentially bind protons, requiring pKa2 ≤ pKa1, restricts the sample space (gray area excluded). Although the blue and orange traces (pKa2 = 4 and 5, respectively) retain the behavior of the 8-state model, symport is not observed for pKa2 ≥ 7.0 for any value of Roff, and the transporter approaches stoichiometric transport at high values of pKa2, reflecting a strong bias toward antiport for the 10-state model under these particular conditions and constraints.
The 10-state model is biased toward antiport when driven solely by a pH gradient. We varied the second protonation value, pKa2, to examine how this parameter affects transport in the 10-state model. Here, pKa2 = 4, blue; 5, orange (overlapped with blue); 7, yellow; 7.5, purple; 8, green; and 9, cyan. Unlike the 8-state model, where inverting the rates for an efficient antiporter can produce an equally efficient symporter, the 10-state model is asymmetric. The requirement that EmrE sequentially bind protons, requiring pKa2 ≤ pKa1, restricts the sample space (gray area excluded). Although the blue and orange traces (pKa2 = 4 and 5, respectively) retain the behavior of the 8-state model, symport is not observed for pKa2 ≥ 7.0 for any value of Roff, and the transporter approaches stoichiometric transport at high values of pKa2, reflecting a strong bias toward antiport for the 10-state model under these particular conditions and constraints.
Effect of pH on steady-state transport phenotypes
Next, we examined the influence of environmental conditions on net transport. In our simulations, the energy required to drive coupled transport is stored in the proton gradient. For perfectly coupled stoichiometric transport, a given ΔpH will drive a set substrate gradient according to Eq. 8. However, in free-exchange transport, the degree of proton/drug coupling is inherently influenced by the exact internal and external pH values. As proton on-rates depend on both the proton on-rate constant and the proton concentration, a change in pH affects the distribution of the key states and the partitioning between different pathways. Thus, even for a constant ΔpH, a change in mean pH alters the balance of antiport, symport, and uncoupled uniport.
To investigate this phenomenon, we ran simulations in the 8-state and 10-state models, holding the rate constants while varying pH. The rate constants were chosen to favor antiport using EmrE-like rates for both models (Table 3, column 5 and 6, for the 8- and 10-state model, respectively). Internal pH was held at physiological levels (pHint = 7.4) while external pH was varied 2 units higher or lower. Fig. 9 shows how the two models diverge in behavior. Once again, the 8-state model displays symmetric behavior, with an inverted pH gradient leading to an inverted Tr. Interestingly, this is not the case for the 10-state model, which drives a much larger drug gradient with an acidic external environment (drug efflux, lefthand side of Fig. 9) than with a basic external environment (drug uptake, righthand side of Fig. 9). This reveals that a 10-state transporter is a better antiporter under physiological conditions than it is with an unnatural inverted pH gradient, providing a possible failsafe to resist backflow of drug into a cell when the cell is exposed to a basic external environment.
The 10-state model drives more efficient efflux than uptake under physiological conditions. Unlike other simulations, internal pH was held constant at a physiological value (pHint = 7.4), while external pH was varied. For the 8-state model (orange trace, EmrE-like rates, Table 3), symmetric transport behavior is observed for external pH values above and below the internal pH of 7.4. In the 10-state model (blue trace, EmrE-like rates, Table 3), a much larger drug gradient is achieved when external pH is lower than internal pH.
The 10-state model drives more efficient efflux than uptake under physiological conditions. Unlike other simulations, internal pH was held constant at a physiological value (pHint = 7.4), while external pH was varied. For the 8-state model (orange trace, EmrE-like rates, Table 3), symmetric transport behavior is observed for external pH values above and below the internal pH of 7.4. In the 10-state model (blue trace, EmrE-like rates, Table 3), a much larger drug gradient is achieved when external pH is lower than internal pH.
How an antiporter can become a symporter
The W63G point mutation of EmrE abolishes classic WT substrate specificity and replaces it with resistance to macrolide antibiotics such as erythromycin. However, it also confers concentrative uptake of aliphatic polyamines into E. coli (Brill et al., 2012). This combination of erythromycin export and polyamine import means that W63G-EmrE must switch transport direction based on substrate identity alone. While it is not experimentally resolved whether the polyamine import phenotype is the result of proton-coupled symport or of uniport with positively charged polyamines driven into the cell by the negative-inside membrane potential, here we explore how a single transporter may switch between coupled antiport and coupled symport using the 10-state model.
For EmrE, the identity of the bound drug can change the alternating-access rate over nearly two orders of magnitude (Morrison and Henzler-Wildman, 2014). Additionally, EmrE can bind drug with affinities ranging over five orders of magnitude, with drug-binding affinity determined by off-rate for those substrates that have been studied in detail (Adam et al., 2007), and the drug off-rate varies with protonation state of the transporter (Robinson et al., 2017). Thus, we completed simulations varying all drug-dependent rate constants (, , , , and ) over reasonable physiological ranges around the known values for EmrE. Since pKa2 must be <7 to allow for symport in the 10-state model, we ran two simulations (Table 3, columns 7 and 8): one with values estimated for WT EmrE (Fig. 10 A, pKa1 = 8.2 and pKa2 = 7) and one with lower pKa values (Fig. 10 B, pKa1 = 7.0, pKa2 = 5.0), closer to what is expected for a glutamate residue in aqueous solution. These figures are graphed in 2D space by collapsing alternating-access rates and drug/proton off-rates as ratios. As expected, no combination of drug-induced rates can drive symport when using values estimated for WT EmrE (Fig. 10 A) under these conditions. However, with sufficient lowering of both pKa values, coupled antiport and symport can coexist in a single transporter (Fig. 10 B). This simple scheme allows for the identity of transported drug to determine the type of proton-coupled transport, a striking result.
Drug identity can trigger a switch from efflux to influx. Four rate constants may vary depending on the identity of the transported drug (, , , and ). We varied these rate constants over a physiological range to explore whether different combinations of these parameters (to mimic transport of different drugs) can induce both symport (Tr < 1, pink) and antiport (Tr > 1, orange) of different drugs by the same transporter. (A) Using pKa values estimated for WT EmrE (pKa1 = 8.2 and pKa2 = 7), antiport dominates the parameter space regardless of drug-dependent rate constants when transport is driven by a pH gradient alone. (B) By lowering the pKa values (pKa1 = 7.0, pKa2 = 5.0) for proton binding by the transporter, different values of the drug-dependent rate constants can result in either symport or antiport, even though the transporter-specific parameters are held constant, reflecting the potential for a single transporter to perform both proton-coupled antiport and symport of different substrates.
Drug identity can trigger a switch from efflux to influx. Four rate constants may vary depending on the identity of the transported drug (, , , and ). We varied these rate constants over a physiological range to explore whether different combinations of these parameters (to mimic transport of different drugs) can induce both symport (Tr < 1, pink) and antiport (Tr > 1, orange) of different drugs by the same transporter. (A) Using pKa values estimated for WT EmrE (pKa1 = 8.2 and pKa2 = 7), antiport dominates the parameter space regardless of drug-dependent rate constants when transport is driven by a pH gradient alone. (B) By lowering the pKa values (pKa1 = 7.0, pKa2 = 5.0) for proton binding by the transporter, different values of the drug-dependent rate constants can result in either symport or antiport, even though the transporter-specific parameters are held constant, reflecting the potential for a single transporter to perform both proton-coupled antiport and symport of different substrates.
Discussion
Transporters have been traditionally classified as antiporters, symporters, or uniporters. Mechanistic models of transporters generally reflect these strict classifications and include only pathways that allow for stoichiometric coupled transport (Lolkema and Slotboom, 2019; Oh and Boudker, 2018; Stein, 1986). Recently, improved experimental methods applied to a broader set of transporters have revealed that some transporters cross these boundaries and do not fit cleanly within a single class (Bazzone et al., 2017; Bozzi et al., 2019; Dohán et al., 2007; Nguitragool and Miller, 2006; Robinson et al., 2017). In light of this, a new generalized model of transport is required that can simultaneously accommodate all transport modes. We initially developed an unrestricted free-exchange model to account for all the observed states and transitions of EmrE (Robinson et al., 2017). The free-exchange model theoretically allows this proton-coupled drug efflux pump to perform antiport, symport, and uniport. Here, we have shown that such an unrestricted model can describe the antiport phenotype seen in EmrE (Fig. 10 A), and in fact the second proton binding event favors antiport (Fig. 8) and enhances the efficiency of antiport relative to symport under these simple ΔpH-only conditions (Fig. 9). These simulations can also recapitulate the curious phenotype of W63G (Brill et al., 2012), a point mutant of EmrE in which transport direction reverses based on the identity of the transported drug (Fig. 10 B).
Most importantly, we have shown that highly coupled transport can be achieved in the free-exchange model with minimal biasing of rate constants (Figs. 7 and 8). The simulations also show that the particular combination of rate constants may result in a transporter that has robust behavior that does not change under different environmental conditions or may switch transport behavior with changing environmental conditions (Fig. 9). This demonstrates the utility of a free-exchange model for systems requiring consideration of “minor” states/transitions and demystifies how substrate and ion can be coupled without restrictions on transporter states and transitions. Nevertheless, free exchange transport is inherently less energetically efficient than stoichiometric transport mechanisms. Here, we consider the potential benefits of a free-exchange model in comparison with a traditional tightly coupled mechanism to begin to understand why some transporters appear to follow each type of mechanism.
Evolution
Evolution selects for coupling tailored to the needs of a particular biological system (Henderson et al., 2019). For example, mammals regulate sugar availability at the organismal level. Consequently, the mammalian glucose transporter (GLUT) family of hexose transporters function as sugar uniporters, with a few tissue-specific exceptions. In contrast, microbes often have to survive in environments with unpredictable nutrient availability. Thus, many microbial homologues of the GLUT transporters appear to be tightly coupled sugar/proton symporters, allowing efficient concentrative sugar import (Walmsley et al., 1998; Wilson-O’Brien et al., 2010; Mueckler and Thorens, 2013). Interestingly, the GLUT homologue GlcP from Staphylococcus epidermidis appears to represent an intermediate case. It employs a free exchange mechanism to perform both proton-coupled sugar symport and sugar uniport depending on external pH (Bazzone et al., 2017). These examples of sugar transporters demonstrate how each have likely evolved to maintain the degree of coupling sufficient for their function in the host organism.
While sugar symporters represent an instance where imperfect coupling is sufficient, loose coupling may be required for multidrug antiporters. Observations of ATP-driven multidrug transporters reveal that futile cycles of ATP-hydrolysis occur between productive drug efflux events and that this may be a trade-off required to achieve multidrug recognition (Al-Shawi et al., 2003; Sharom et al., 1995). Thus, it was predicted that proton-driven multidrug transporters may also sacrifice efficiency to achieve multidrug recognition (Krupka, 1999a,b). The ability to export diverse toxic substrates is critical to ensure survival, and thus would be favored evolutionarily, even at the expense of perfect efficiency. A second potential advantage of a free exchange mechanism involves efficient substrate release. Multidrug transporters recognize and transport chemically diverse molecules, and the binding affinities (and thus off-rates) can range over five orders of magnitude in the case of EmrE (Morrison and Henzler-Wildman, 2014). This presents an issue for tight binding substrates, where slow off-rates may cause tight binding substrates to become “stuck” on the transporter if not for the ability to simultaneously bind proton, which reduces the affinity and enhances the drug off-rate. This idea is supported by Gillespie simulations of EmrE that can resolve the exact pathways for transport (Robinson et al., 2017). This flexibility is not possible in pure-exchange models of transport (Fig. 1) but is possible within the free exchange (Figs. 2 B and 3), and may be a property that is selected for by evolution, by enabling continued efficient transport of toxins out of the cell.
Even for transporters with apparently perfect stoichiometric transport like LacY, single point mutations can produce leak pathways (Forrest et al., 2011; Guan and Kaback, 2006; Varela and Wilson, 1996). The fine-tuning required to achieve stoichiometric transport in naturally occurring transporters may help to explain the relatively loose coupling exhibited by the de novo–designed zinc/proton exchanger Rocker (Joh et al., 2014). However, this suggests that there may be a low barrier for evolution from a tightly to a loosely coupled transport regimen, and thus, tightly coupled systems could become “scaffolding” to design new free-exchange transporters. In fact, this appears to have happened naturally in the small multidrug resistance transporter family (Kermani et al., 2018).
Voltage in the proton-motive force
The proton motive force that drives proton-coupled transport in vivo includes both the proton gradient (ΔpH) and the transmembrane voltage (ΔΨ). Indeed, coupled antiport in EmrE can be driven by either ΔpH or ΔΨ alone or in combination (Rotem and Schuldiner, 2004; Robinson et al., 2018b; Yerushalmi et al., 1995). One limitation of the current free-exchange model is that we consider only ΔpH and not ΔΨ. This choice was based on the availability of experimental measurements of rates for EmrE at different pH values, allowing us to more reliably model the effect of ΔpH. However, since alternating access moves both charged substrates and charged residues of EmrE across the membrane, alternating-access rates are certainly impacted by ΔΨ. In addition, the binding of charged substrates can be affected by voltage as well, if the binding process effectively moves a charged substrate partway down the voltage gradient (Garcia-Celma et al., 2009). Unfortunately, despite the ability of voltage gradients to drive transport, the effect of voltage on individual steps in the transport cycle is unclear (Forrest et al., 2011). New research probing the effect of voltage on all steps in the transport cycle is needed to elucidate how voltage influences the microscopic rate constants required to model transport.
Overall, modeling voltage presents new possibilities to predict transport under more conditions and explain some phenotypes of EmrE. For example, WT EmrE has been seen to move proton and drug in the same direction under voltage alone, suggesting the ability to reverse the flux of traditionally antiported substrates (Robinson et al., 2017). Voltage may also enhance the efficiency of electrogenic coupled transport by further biasing relative flux throughout certain pathways. For example, the negative-inside potential could speed up proton on-rates and slow proton off-rates on the periplasmic side of the membrane, resulting in faster turnover of drug. Overall, more complex phenotypes may occur when both ΔΨ and ΔpH are present. This is the subject of future effort in our laboratory to acquire the necessary kinetic data to expand the model to include voltage in a biologically relevant manner.
Conclusions
Research into free exchange models of transport has broad implication for protein design. By understanding the requirements for different transport regimes, and how to switch between them, researchers can design de novo transporters or manipulate existing transporters to switch behavior under different pH, drug, or other environmental conditions. Overall, our understanding of mechanisms not as a singular pathway but as a superposition of many possible outcomes allows us to further investigate the boundaries of transporters, understand the physiological behavior of these important proteins, and engineer novel systems.
Online supplemental material
The supplemental information includes the matrix form of the differential equations (Eqs. 1 and 2) as well as the Matlab files for the kinetic model. All of the Matlab files for the numerical simulations, including the specific parameters used to produce each of the figures in this paper, are freely available on Github.
Acknowledgments
Merritt C. Maduke served as editor.
We thank Hallie Hanson for assistance writing the Matlab code.
Research reported in this publication was supported by National Institutes of Health grant R01GM0958339 to K A. Henzler-Wildman. G A. Hussey was partially supported by the Hilldale Undergraduate Research Fellowship at University of Wisconsin–Madison and N.E. Thomas by National Institutes of Health grant T32GM007215. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
The authors declare no competing financial interests.
Author contributions: The project was conceived by K A. Henzler-Wildman. Work was carried out by G A. Hussey with advice from K A. Henzler-Wildman and N.E. Thomas. Results were analyzed and manuscript was written by K A. Henzler-Wildman, G A. Hussey, and N.E. Thomas.





![Simulated liposomal flux assay. Simulations are conducted as virtual liposomal flux assays. The simulation begins with a 10-fold proton gradient and identical drug concentration inside and outside the proteoliposome. We assume infinite buffering capacity, so the proton gradient, represented as Hr, remains constant throughout the simulation. Unless otherwise indicated, Hr is set at 10. The simulation is then run until the drug concentration reaches steady state. Transport outcome is assessed by Tr, or the ratio of internal to external drug concentration at steady state (Tr = [Drug]int/[Drug]ext).](https://cdn.rupress.org/rup/content_public/journal/jgp/152/1/10.1085_jgp.201912437/3/m_jgp_201912437_fig4.png?Expires=1769093983&Signature=Clni5TrNQNUvtcv1r9fQFVQUuosDuJMlQBD4kX1K4x27OnxEeNo8Aic6UN5Gv~ctKvTpqKrak~QXVid5KYCBRNgNBevd33evZr3ZlDRR8~~msE-tRkb3WH8ahW2yDrMHa3QRuBgUfiNS8AsnxuOggFggyGzi-y8bIgtY1z~n6TMk4AoFpJQsvdPIa5PZbT~NclBqreEZxIoWiX-U7LaNhOas75qHezX3OlDRDyEI~7y7Uerurm12wc57Lwg1fpRg3-CfRr1Pe7vKwbDk8AmcqFuyr7sV5-6KXFKgIRQzGFy23fhJ2dbpQRG4tx1hf7xzmMX-NBgKeYGRPazGhk19fw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)