Mechanism of hydrophobic gating in the acetylcholine receptor channel pore

Neuromuscular acetylcholine receptors (AChRs) expressed at the vertebrate nerve–muscle junctions are ligand-gated ion channels (LGICs) comprised of five subunits, two α1 and one each of β, δ, ε, or γ. The two neurotransmitter binding sites (TBS) are located at interfaces between α–δ and α–ε (adult) or α–γ (fetal) subunits in the extracellular domain (Unwin, 2013). The ion channel pore is formed by M2 helices of the five subunits in the transmembrane domain (TMD). AChRs belong to a superfamily of LGICs that play critical roles in nervous system functions including attention, memory formation, auditory responses, and muscle contraction (Dani, 2015). They are implicated in many human diseases, including Alzheimer’s, schizophrenia, depression, epilepsy, and congenital myasthenia syndrome (CMS; Schaaf, 2014).

AChRs are typical allosteric proteins (Karlin, 1967; Auerbach, 2010; Changeux, 2018) that bind agonists with low affinity in a resting, closed-channel conformation (C). Agonist binding promotes a global “gating” conformational change that sets the receptor in an active, open-channel conformation (O) and rearranges the channel pore to allow ion conduction. Energy changes associated with agonist binding to the TBS have been extensively investigated (Cohen et al., 1991; Brejc et al., 2001; Purohit et al., 2012; Auerbach, 2013; Cecchini and Changeux, 2015; Nayak et al., 2016), but the corresponding energy and structural changes in the pore associated with C↔O gating transition are less thoroughly studied (Jha et al., 2009).

In ion channels, various mechanisms, including steric hindrance by a rigid body (voltage-gated K⁺ channel; Yellen, 2002), pore occlusion by aromatic amino acids (bacterial ELIC channel; Hilf and Dutzler, 2008; Gonzalez-Gutierrez and Grosman, 2010), and an electrostatic barrier due to salt bridges across the pore (OmpA; Hong et al., 2006), have been proposed to regulate ion flow. In AChRs, a girdle of hydrophobic amino acid residues in the middle of the channel pore was proposed to prevent ion permeation in the closed state based on early simulations of the Torpedo AChR structure (Unwin, 2005; PDB ID: 2BG9). Though the pore was wide enough to allow completely stripped cations, the region presented an energy barrier to the permeation of ions owing to (1) permeant cations could not readily shed their first hydration shell in the absence of favorable polar surfaces at the hydrophobic girdle (Miyazawa et al., 2003; Beckstein and Sansom, 2006,) and (2) the constricted hydrophobic surface at the gate in the closed state resulted in capillary evaporation of water, leading to local dewetting of the pore and vapor lock (Rasaiah et al., 2008; Aryal et al., 2015). This was described as a “hydrophobic gate.” In contrast, a sterically closed gate is too constricted to prevent the flow of dehydrated or stripped ions. Hydrophobic gating has been proposed in other ion channels including aquaporins (Burnham and English, 2017), K⁺ channels (Aryal et al., 2014), mechanosensitive channel MScL (Spronk et al., 2006), and LGICs, including GLIC (Zhu and Hummer, 2012), 5HT3 (Yuan et al., 2016), GlyR (Cerdan et al., 2018), and the neuronal α7 AChRs (Noviello et al., 2021).

In the recently solved cryo-EM structures of Torpedo AChRs (PDB ID: 6UWZ [Rahman et al., 2020], 7QKO, and 7QL6 [Zarkadas et al., 2022]), a broad region between residues L9′ and L16′ (numbering by residue position starting from the intracellular helix boundary) in the M2-helices has been implicated to form the hydrophobic gate that prevents ion flow. The narrowest part in this region with ∼3 Å diameter in the apo structure (PDB ID: 7QKO) is unlikely to act as a steric gate to prevent ion flow. Therefore, it will be interesting to explore the chemico-physical nature of the gate in the closed state and during the channel opening transition in the neuromuscular AChR model system.

Mutations in some of the residues in this region including L9′, S/T12′ (Croxen et al., 1997; Webster et al., 2004; Gomez et al., 2002), and V13′ (Engel et al., 1996) have been linked to human congenital myasthenia (CMS) and lethal multiple pterygium syndrome (Engel et al., 2015). There have been several attempts to study the kinetics and energetics of these key pore mutations by various experimental methods (Giraudat et al., 1986; Leonard et al., 1988; Villarroel et al., 1991; White and Cohen, 1992; Akabas et al., 1994; Cymes et al., 2005; Wang et al., 2008; Jha et al., 2009; Gupta et al., 2017,). Some of these mutations in the AChR pore increase constitutive channel opening (Filatov and White, 1995; Ohno et al., 1995; Purohit and Auerbach, 2009,), but its mechanism is unclear. Do these mutations make wetting of the pore more favorable by changing its physico-chemical profile or result in pore widening by conformational change or both? Based on structural studies, it has been proposed in some related LGICs that the M2 helices undergo radial tilting and rotation during the C↔O gating transition, which results in overall dilation of the pore (Hibbs and Gouaux, 2011; Sauguet et al., 2013). Conversely, under ambient conditions in constricted nanopores, water undergoes a liquid–vapor phase transition that is sensitive to the pore radius, and surface and chemical properties of the pore residues (Yazdani et al., 2020). Therefore, understanding the function of the gate requires a thorough investigation of the thermodynamic properties of the gate residues as a function of their chemical nature and/or the conformational changes that happen at the gate during the channel C↔O transition.

Here, we adopted a multipronged approach (protein engineering, single channel kinetics, and molecular dynamics simulations) to investigate the chemical nature of the amino acids, the local structural rearrangements, and intersubunit interactions that underlie gate opening in AChRs. We present evidence of a hydrophobic barrier which suggests that both conformational change and a wetting transition of the gate in the pore lead to channel opening. We estimate the energy barrier to ion flux at the gate by molecular simulations and elucidate the role of side-chain chemical properties and intersubunit interactions in the regulation of the channel-opening transition. The results provide insights into the gating mechanism of AChRs.

Human embryonic kidney (HEK) 293 cells were maintained in Dulbecco’s minimal essential medium (DMEM) supplemented with 10% fetal bovine serum and 1% penicillin–streptomycin, pH 7.4. The cultures were incubated at 37°C and 5% CO₂. The QuikChange site-directed mutagenesis kit (Agilent Technologies) was used to incorporate mutations in the mouse AChR subunit cDNAs, which were verified by nucleotide sequencing. HEK cells were transiently transfected by calcium phosphate precipitation method with 2.5 μg of cDNA per 35-mm culture dish in the ratio of 2:1:1:1 (α:β:δ:γ). Most electrophysiological experiments were done ∼24 h after transfection.

Single-channel currents were recorded at room temperature (∼23°C) in the cell-attached patch configuration. The cells were bathed in K⁺-ringer composed of (in mM) 142 KCl, 5.4 NaCl, 1.8 CaCl₂, 1.7 MgCl₂, and 10 HEPES/KOH (pH 7.4). The patch pipettes were filled with Dulbecco’s phosphate-buffered saline (PBS) containing (in mM) 137 NaCl, 0.9 CaCl₂, 2.7 KCl, 1.5 KH₂PO₄, 0.5 MgCl₂, and 8.1 Na₂HPO₄ (pH 7.3/NaOH). Most of the experiments in this manuscript have been performed in the absence of any agonists (unliganded gating). In liganded experiments, agonists were added to the pipette solution from a stock solution to obtain the desired concentrations.

Patch pipettes were fabricated from borosilicate glass, coated with sylgard (Dow Corning), and fire-polished to a resistance of ∼10 MΩ when filled with pipette solution. Single-channel currents were recorded using a PC505 amplifier (Warner Instruments), low-pass filtered at 20 kHz, and digitized at a sampling frequency of 50 kHz using a NI data acquisition board (SCB-68, National Instruments). The pipette holder and pipettes used for the unliganded experiments were never exposed to agonists.

Kinetic analyses were performed by directly fitting kinetic models to idealized single-channel current data using the QUB software suite (Nicolai and Sachs, 2013). For estimation of rate constants, clusters of single channel activity, flanked by ≥20 ms non-conducting periods, were selected by eye. The clusters were digitally filtered at 12 kHz and then idealized into noise-free intervals by using the segmental K-means (SKM) algorithm (Qin et al., 1996). The forward (f_n) and backward (b_n) gating rate constants were estimated from the idealized intracluster interval durations by fitting with a simple kinetic C↔O scheme using a maximum-interval likelihood (MIL) algorithm after imposing a fixed dead time (τ_d) of 50 μs (Qin et al., 1997). MIL algorithm allowed for choosing a dead time which might be several times the briefest mean dwell time duration in the data without compromising the accuracy in rate determination (Qin et al., 1996 ). Hence, our choice of dead time did not limit our ability to accurately determine fast kinetic rates. In our hands, rate constants could be accurately estimated from intracluster intervals in the range of ∼10 to ∼10,000 s⁻¹. The unliganded gating equilibrium constant was given by E₀ = f₀/b₀. The intrinsic gating energy or the unliganded gating energy change for a mutation was given by ΔG₀ = −RT*ln (E₀), where R = universal gas constant (0.001987 kcal.K⁻¹.mol⁻¹), T = absolute temperature (296 K), and RT = 0.59 kcal mol⁻¹. In our experiments, we can accurately measure twofold change in E₀ or ± 0.4 kcal mol⁻¹ change in ΔG₀.

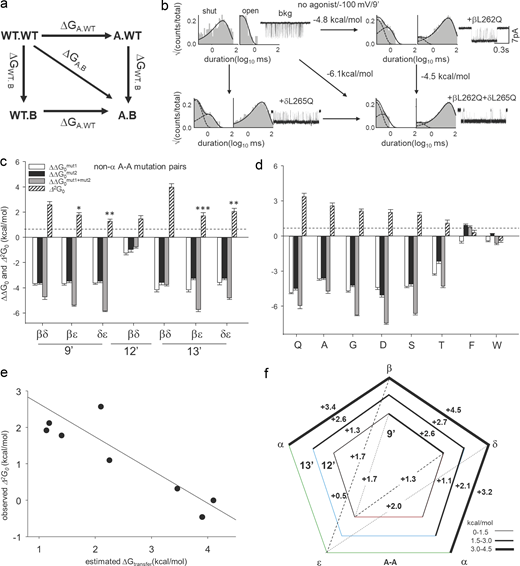
We strategically introduced combinations of gain/loss-of-function mutations in AChRs to obtain rate constant values in the measurable range of patch-clamp (Jadey et al., 2011). We added background perturbations (mutations and depolarization) that only changed the unliganded gating equilibrium constant by known extents. The observed E₀/ΔG₀ values were corrected by the fold/ΔΔG₀ caused by the background to obtain the changes in ΔG₀ for the wild-type (WT) condition at −100 mV. For most of the data presented here, we have consistently used a combination of αA96H and αY93H as the background (Nayak et al., 2012). This double mutant caused an ∼44,700-fold increase in E₀ and lowered the WT ΔG₀ (+8.3 kcal mol⁻¹; Nayak et al., 2012) by −6.31 kcal mol⁻¹ (−0.59*ln [44,700]), resulting in ΔG₀^bkg = 1.99 kcal mol⁻¹ (see Table S2). To obtain the ΔΔG₀^mut values for any gate mutation (e.g., for βL262A), the background ΔG₀^bkg (1.99 kcal mol⁻¹) was subtracted from the observed ΔG₀ (−1.69 kcal mol⁻¹ for βL262A measured on αA96H + αY93H background), i.e., ΔΔG₀^mutant = ΔG₀(mutant + background) − ΔG₀(background). ΔΔG₀ for βL262A = (−1.69) − (1.99) = −3.68 kcal mol⁻¹ (see Table S2). A few other mutant combinations were occasionally used as background to obtain the ΔΔG₀ values associated with the gate residue mutations (see Table S2).

The kinetics of unliganded gating activity can be complex (Jackson et al., 1990; Grosman and Auerbach, 2000; Purohit and Auerbach, 2009), with multiple exponential components in the dwell-time distributions. Therefore, for estimation of rate constants of unliganded gating, additional C and O states were added to the simple C↔O scheme, one at a time, until the log-likelihood score failed to improve by >10 U. The unliganded gating opening and closing rate constants (f₀ and b₀) were determined from the values associated with the predominant (≥80%), briefest component of each dwell-time duration distribution histogram. This approach is justified due to the following reasons: (1) aromatic amino acid mutations of the TBS (such as αY93H and αY198F) eliminated the longer, less frequent open component without affecting the main gating component (Purohit and Auerbach, 2010); (2) ΔG₀ values measured from the briefest components correspond to the predicted ΔG₀ values, even for combinations of mutations. For example, for a combination of five mutations (αA96F + βT456I + δI43Q + εE181T + εL269F; see Table S2 in Nayak et al. [2012]), the total predicted gain of function is equal to 25,22,101 folds over the WT AChRs. Fold changes for this combination were measured from liganded experiments, assuming the fold changes in E₂ in the presence of ligands (ACh/Cho) are due to changes in allosteric constant E₀ only (αA96F = 497, βT456I = 3.0, δI43Q = 4.5, εE181T = 2.1, εL269F = 179 folds). For this combination, the expected E₀ = fold change × WT E₀ = 25,22,101 × (7.4 × 10⁻⁷) = 1.87. The experimentally observed E₀ = 1.37 ± 0.14 (Nayak et al., 2012). Accordingly, the predicted and observed ΔG₀ values were −0.37 and −0.19 kcal mol⁻¹, respectively. This concurrence between the predicted and observed values within an error limit of ±0.4 kcal mol⁻¹ proves beyond doubt the accuracy in determining the E₀ and ΔG₀ by using the briefest major component while eliminating the longer, less frequent component of unliganded gating.

In AChRs, neighboring amino acid residues (within <15 Å) can potentially interact locally during C↔O gating (Gupta et al., 2017). If two residues involved in gating are energetically coupled, their free energy changes are non-additive (combined change in double mutant is different from the sum of individual changes; Ranganathan et al., 1996; Sine, 2012). Thermodynamic MCA is a well-established method to measure inter-residue coupling or independence in ion channels (Yifrach and MacKinnon, 2002; Lee and Sine, 2005). We routinely design AChRs with mutations at neighboring residue positions, separately measure free energy changes for single and double mutant AChRs from single channel currents (as described above), and estimate their coupling energies (Δ²G) by using the mutant cycle analysis. For example, the ΔG₀ for βL262Q, δL265Q, and (βL262Q + δL265Q) pair were −4.86, −4.5, and −6.0 kcal mol⁻¹, respectively (background mutations used were αA96H + αY93H, Table S3). Hence, Δ²G for this pair = −6.0 − (−4.9–4.5) = +3.4 kcal mol−¹. Higher order interaction energies (ΔⁿG: n > 2) were calculated as (sum of individual ΔΔG₀ for mutations) − (ΔΔG₀ for the combination). Since the error in ΔG₀ measurement in our experiments is approximately ±0.4 kcal mol⁻¹, the combined error in coupling energy calculation for a mutation pair is √(0.4² + 0.4²) ≈ 0.57 kcal mol⁻¹, assuming independent errors, by the law of propagation of errors. Further, the error in the coupling energy estimate was measured earlier (Gupta et al., 2017) from the SD of experimental values for residues separated by >15 Å, which was 0.56 kcal mol⁻¹. The agreement indicates that the errors in the equilibrium constant estimates are independent. Therefore, we set a threshold of ±0.6 kcal mol⁻¹ for coupling energy values to be significant.

The initial structural coordinates for WT C, and O and the α-Btx bound non-conducting conformations were obtained from recently solved cryo-EM structures of Torpedo AChR (PDB IDs: 7QKO, 7QL6, and 6UWZ, respectively). Though 7QL6 open pore has diffuse densities of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) in the cryo-EM structure and may stabilize the open pore in a manner different from the WT open state, we used this for all our simulations owing to the accuracy in atomic coordinates. The full-length pentameric proteins were embedded in POPC bilayer using CHARMM-GUI (Jo et al., 2008). The systems were solvated with water and the ionic strength was increased by adding 150 mM NaCl. To investigate the role of a hydrophobic gate in Na⁺ ion permeation, L to S mutations at 9′ positions were incorporated in different chains in the closed channel (PDB ID: 7QKO) using CHARMM-GUI.

Initially, all the prepared systems were subjected to a local energy minimization followed by an equilibration of 2 ns by gradually reducing the harmonic restraints applied on the lipid molecules to avoid sudden deformation of the bilayer. Planar restraints were applied on the head group atoms of the lipid molecules whereas dihedral restraints were applied on the unsaturated carbon atoms of oleyl tails of lipid molecules. Subsequently, all the systems were simulated without any restraints for about 150–250 ns (varying with systems) under NPT conditions using standard periodic boundary conditions and minimum image convention. Analysis of various structural properties was performed by averaging over the last 50 ns of the simulation.

All the simulations were performed using NAMD (Phillips et al., 2005) with lipid, proteins, and Na⁺ and Cl⁻ ions parameterized using the CHARMM36m force field (MacKerell et al., 1998). TIP3P model was used for water (Jorgensen et al., 1983). An integration timestep of 2 fs was used while keeping all the covalent bonds involving hydrogen atoms constrained to their equilibrium bond length using the SHAKE algorithm (Ryckaert et al., 1977). The particle mesh Ewald algorithm (Essmann et al., 1995) was used for the calculation of electrostatic interactions. A cut-off of 12 Å with a switching distance of 10 Å was applied for the computation of the real-space part of electrostatic as well as Lennard–Jones interactions. Langevin dynamics (Schneider and Stoll, 1978) were used to maintain the temperature at 310 K while pressure was kept at 1 atm using a Nosé–Hoover–Langevin piston (Feller et al., 1995). Semi-isotropic pressure coupling was used and a constant ratio of x- and y-dimension (orthogonal to membrane normal) of the simulation cell was maintained. All the visualizations were done using VMD software (Humphrey et al., 1996). HOLE (Smart et al., 1996) was used for pore-diameter calculations and visualization of the pore.

We employed well-tempered metadynamics (WT-MTD) simulations for the calculation of the potential of mean force (PMF) profiles for the permeation of a Na⁺ ion through the channel pore utilizing the colvar module of NAMD (Phillips et al., 2005). The initial configurations were taken from the respective unbiased simulation after equilibration. A Na⁺ ion was selectively tagged and its position with respect to the average position of Cα atoms of 9′ residues of the channel subunits along the z axis was considered as the collective variable. The tagged Na⁺ ion was allowed to sample the extra- and intracellular regions through the TMD, with large barrier walls at z ≈ ±35 Å. Another constraint of 100 kcal mol^–1 Å^–2 was applied in xy-plane to confine the sampling of the ion within a 15 Å × 15 Å window around the pore axis. For each system, the WT-MTD simulations were run to collect a sufficiently large number of representative samples of all possible conformations in the landscape to obtain the converged PMF profiles (Domanski et al., 2017). Typically, about 0.8–1 μs simulation run was required for each PMF profile to converge (see Fig. S4 a). In total, we performed >5 μs of simulations for WT and mutated systems.

Fig. S1 shows the mutational effects of the gate residues. Fig. S2 elucidates correlation plots in support of hydrophobic gating. Fig. S3 represents interactions between gate residues. Figs. S4 and S5 show the results and analysis of data obtained from MD simulations. Videos 1, 2, and 3 show water and ion permeation through an AChR pore in the WT closed, open, and toxin-bound non-conductive state of the receptor. Tables S1, S2, S3, S4, S5, and S6 show the kinetic rates (f₀/b₀), equilibrium constants (E₀), and free energy changes (ΔG₀) for the WT and mutant AChRs, whereas Table S7 describes the details of the simulated systems.

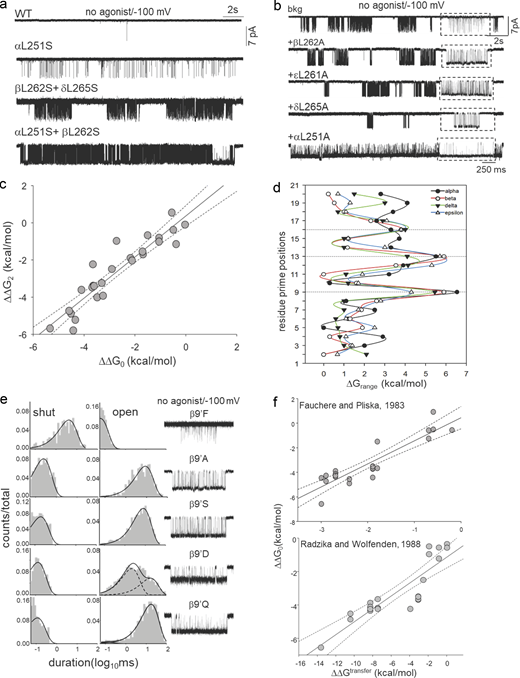
Fig. 1 a shows the multiple sequence alignment of M2 residues, highlighting amino acids that are conserved and homologous. Approximately 55% of the pore residues, including the L9′, V13′, and L16′, are conserved across different species. L9′ is conserved throughout all the subunits except in α5 and β3 (it is V). V13′ is conserved in all the subunits except in β4 (it is F). Likewise, L16′ is conserved in all the subunits except in ε and γ, where it is an F. Fig. 1 b shows synaptic and membrane views of the AChR structure (PDB ID: 7QKO). Fig. 1 c is a helical wheel representation of residues between 8′ and 18′. The L9′, V13′, and L16′ residues face the pore’s aqueous environment, whereas 10′, 11′, and 12′ residues point away from the lumen of the pore.

To study the local structure at the gate, we compared recently solved cryo-EM structures of Torpedo AChRs with PDB IDs: 7QKO, 7QL6 (Zarkadas et al., 2022), and 6UWZ (Rahman et al., 2020). 7QKO is in an apo-resting state, 6UWZ represents an α-bungarotoxin (Btx) bound non-conductive state, and 7QL6 is in a carbmylcholine (CCh)-bound open conformation. Fig. 1 d shows a comparison of the pore dimensions of the apo-closed (7QKO; [C]) versus the open (7QL6; [O]) structures using HOLE diagram (Smart et al., 1996). The inset represents zoomed-in views of the gate showing regions with a diameter ≤4 Å (blue) and ≥4 Å (red). Fig. S1 a shows the change in diameter as a function of the pore coordinates (Å) along the z-axis (axis perpendicular to the membrane surface). The narrowest region in 7QKO (C) has a diameter of ∼3.0 Å at 9′ and 16′ positions. In 7QL6 (O), on average, the pore is wider by ∼4 Å in the same region (diameter ∼7.5 Å). The 6UWZ pore is overall comparable with that of the 7QKO structure except at 16′ where the pore is slightly narrower (Fig. S1 b). Low-resolution structures of neuromuscular AChRs (6 Å resolution) were earlier solved apparently in the apo (PDB ID: 4AQ5) and open/desensitized (PDB ID: 4AQ9) states by electron microscopy of ACh-sprayed and freeze-trapped post-synaptic membranes (Unwin and Fujiyoshi, 2012). We compared 4AQ5 and 4AQ9 with the recent high-resolution structures. The pore of 4AQ5 was much wider compared with 7QKO, with a diameter comparable with 7QL6 and 4AQ9 at 9′ position (Fig. S1 b). The differences in pore dimensions in 4AQ5/4AQ9 structures have been attributed to known magnification and amino acid register errors in the M2 helices (Rahman et al., 2020). Therefore, we did not further use these structures for analysis of the pore architecture and gate function.

To understand the function of the gate residues, we mutated the amino acids at 9′, 12′, 13′, and 16′ positions in all five subunits. In total, we investigated 53-point mutants and 62 mutant combinations by recording single channel currents from “apo” (unliganded) AChRs having these mutations in the absence of any agonists. Fig. 2 a shows representative current recordings from WT AChRs and AChRs with L9′S mutation(s). In the absence of any agonist and at −100 mV membrane potential, the WT AChR rarely opens because of a small (but measurable) unliganded gating (allosteric) equilibrium constant, E₀ = 7.3 × 10⁻⁷ (Nayak et al., 2012). αL251S mutation substantially increased constitutive channel gating activity compared with the WT AChRs. Further, we added 9′S mutations conjointly to either β- and δ- (mutations in two subunits) or α- and β-subunits (mutations in three subunits) and recorded channel activity (Fig. 2 a, bottom traces). Unliganded constitutive channel openings progressively increased with an increasing number of mutations at the 9′ position owing to increases in the frequency of open events and the mean open times (τ_open; Fig. S1 c). The addition of sub-saturating [ACh] (10 μM) to AChRs with point mutations at αL9′ position (A, D, S) resulted in channel open probability (P_o) ∼ 1.0, which cannot be analyzed to gain meaningful kinetic and energetic information about the pore mutations (Fig. S1 d). Even the addition of a low concentration of [ACh] (100 nM) drastically increased the open probability of the mutant channels. The constitutive channel openings and high P_o observed in these mutants may account for basal currents and sustained activation of the synaptic end-plate currents (EPCs) in the presence of the neurotransmitter at the NMJs in slow-channel CMS (Fig. S1 e). Therefore, we performed most of the experiments in the absence of any agonists using appropriate background-engineered mutations to facilitate the measurement of single-channel kinetics by patch-clamp experiments (see Materials and methods and Table S2 for all background mutations).

The average radii of free and hydrated Na⁺ ions are ∼1.02 and 3.5 Å, respectively (Fifen and Agmon, 2019). The narrow hydrophobic girdle between 9′ and 16′ amino acids can provide a steep energetic barrier to the permeant cations as they cannot shed their hydration shell in the absence of polar surfaces at the gate. It is, however, likely that the closed AChR pore with ∼3.0 Å diameter offers a steric barrier to hydrated ion flow. To gain insight into the ion permeation barrier, we mutated the hydrophobic residues and measured the changes in ΔG₀ for each of the above mutations at the gate. From single channel current records, channel opening (f₀) and closing (b₀) rate constants were measured and E₀ = f₀/b₀ and ΔG₀ = −0.59*ln(E₀) were calculated (see Materials and methods). Fig. 2 b shows representative single channel currents for Ala mutants of the L9′ residues (in the presence of suitable background mutations) in α, β, δ, and ε subunits in the absence of agonists. The openings occurred in clusters, with the intervening long silent periods reflecting desensitization (Purohit and Auerbach, 2009). Table S1 shows free energy changes (ΔΔG₀) in the mutant versus WT AChRs. For some of these mutations, ΔΔG₂ values (free energy changes in the presence of AChRs with both binding sites saturated with agonists) were reported previously (Jha et al., 2009; Purohit et al., 2013) and are presented in Table S1. Fig. 2 c is a scatter plot showing the correlation between ΔΔG₀ versus ΔΔG₂ for different mutations at 9′, 12′, 13′, and 16′ positions. The slope of the linear regression was 1.0 ± 0.09 (Fig. 2 c), indicating that the changes in liganded gating energy due to the gate mutations are due only to a change in the intrinsic or unliganded gating energy. That is, none of the mutations changed the “coupling” constant, which is the ratio of agonist equilibrium dissociation constants, C versus O. To visualize the energy changes in the pore region during C↔O gating transition, we plotted the range of liganded (ΔG₂; reported previously (Jha et al., 2009; Purohit et al., 2013) and unliganded energy changes (ΔG₀; from the present work) for all the pore residues versus their prime positions in the pore (Fig. 2 d; see Materials and methods). In α, β, δ, and ε subunits, the maximum free energy changes were observed at 9′, 13′, and 16′ positions (marked by a dotted line).

It has been proposed that drying (dewetting) of the pore in the vicinity of the hydrophobic girdle leads to channel closing (Zhu and Hummer, 2012). Conversely, wetting of the pore would be associated with channel opening. We hypothesize that wetting–dewetting of the pore is contingent on the local environment and side chain conformations of the amino acids. Accordingly, we substituted L9′ and V13′ with hydrophobic, hydrophilic, acidic, and neutral side chains (including those which cause CMS). The ΔΔG₀ values for these mutations were correlated with the changes in standard chemical transfer free energy (ΔΔG^trans) obtained from two widely used hydrophobicity scales (Fauchere and Pliska, 1983; Radzicka et al., 1988). ΔΔG^trans refers to the free energy change associated with the transfer of an amino acid side chain from a hydrophobic to a hydrophilic environment or vice versa, which may be estimated or experimentally determined by measuring the energy cost of transferring an amino acid from oil to water or protein core to an aqueous environment (Simm et al., 2016). A hydrophobicity scale predicts the relative hydrophobicity of all the 20 naturally occurring amino acids based on their ΔΔG^trans. They are useful in predicting the protein secondary structure boundaries in the membrane and hydrophobic regions in proteins based on their sequences. Fig. 2 e illustrates representative current traces and dwell-time duration distribution histograms for some of the amino acid substitutions at βL9′. Table S2 shows the kinetic and energetic consequences (f₀, b₀, E₀, and ΔΔG₀) of mutations at 9′, 12′, 13′, and 16′ positions. Fig. 2 f shows plots of ΔΔG₀ versus ΔΔG^trans values obtained from the two hydrophobicity scales from above (Fauchere and Pliska, 1983; Radzicka et al., 1988). The plots show linear correlation (y = mx + c; m = slope; and c = intercept), with slopes of the linear regression lines passing through the scatters being 1.88 ± 0.2 (R² = 0.81; Fig. 2 f, upper) and 0.39 ± 0.04 (R² = 0.75; Fig. 2 f, lower). The linear correlation indicates that the free energy associated with the transfer of hydrophobic amino acids at 9′ and 13′ positions (WT or mutated side chains) to an aqueous environment of the channel pore underlies the observed gating free energy changes. To further explore the role of the accessible surface area of amino acids in the observed hydrophobic effect, we replotted ΔΔG₀ versus ΔΔG^trans values (Fig. S1 f) using the hydrophobicity scale from Radzicka et al. (1988), but corrected for amino acid side chain head group volumes (Sharp et al., 1991). The correlation between ΔΔG₀ versus ΔΔG^trans significantly improved (R² = 0.87) indicating the significance of the hydrophobic effect in gating rearrangement during channel opening transition.

The pore-forming helices have several hydrophobic residues at positions other than at 9′, 13′, and 16′ (in α: 3′L, 5′I, 8′L, 11′L, 14′F, 15′L, 17′V, and 18′I). Fig. S2 (left) shows correlation plots of ΔΔG₀ versus ΔΔG^trans values for α-, β-, δ-, and ε-subunits at 9′, 13′, and 16′ positions. Fig. S2 (right) are the corresponding correlation plots of ΔΔG₀ versus ΔΔG^trans values at all other positions between 2′ and 18′. There was no discernible correlation between ΔΔG₀ versus ΔΔG^trans values at other hydrophobic residues. These results highlight the significance of the hydrophobic residues at 9′, 13′, and 16′ positions in the gating of AChRs.

We hypothesize that strong intersubunit interactions guide local C↔O conformational changes at the gate. MCA was performed to measure coupling energies (Δ²G₀: second-order coupling energy) to study the interaction between pairs of neighboring residues at the AChR gate (Fig. 3 a; see Materials and methods). Residues located >15 Å away from each other have negligible coupling energies (<0.6 kcal mol⁻¹) in neuromuscular AChRs (Gupta et al., 2017). Fig. 3 b shows a representative result for Q–Q mutation pairs at β9′ and δ9′. The Δ²G₀ for this pair was large, +3.4 kcal mol⁻¹ (see Materials and methods). We measured Δ²G₀ values for 23 unique pairs of Ala and non-Ala substitutions at the 9′ position (Table S3). Fig. 3 c shows the Δ²G₀ values measured for A–A substitutions in β, δ, and ε at 9′, 12′, and 13′ positions. At 9′ and 13′ positions, Δ²G₀ values between neighboring βδ-subunits were significantly greater than the non-neighboring βε- and δε-subunits.

Coupling energy between residues facing the aqueous channel is a function of changes in both non-covalent interactions with other side chains and solvation caused by local water molecules. To separate these component energies and investigate the role of side chain chemical properties in determining intersubunit interactions, we incorporated different mutation pairs at the 9′ position (see Table S3) and measured Δ²G₀ (Fig. 3 d). Fig. 3 e shows a correlation plot between Δ²G₀ for the various side chain substitutions in β and δ with the ΔG₀^trans for hydrophobic side chains (Karplus, 1997). The slope of the linear regression was −1.043 ± 0.18, indicating an almost perfect, inverse correlation between Δ²G₀ and side chain hydrophobicity.

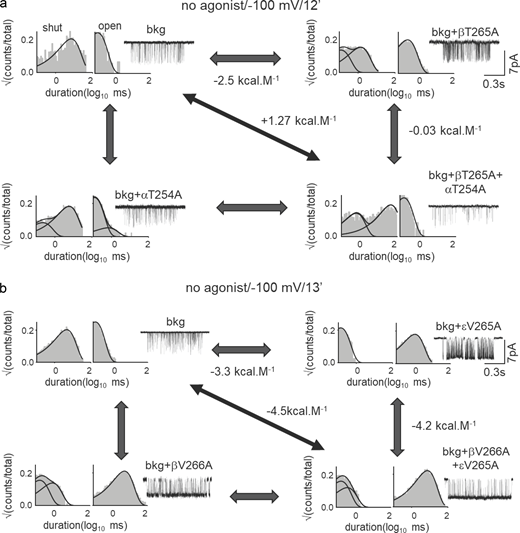
Next, we measured Δ²G₀ values for different side chains at 12′ and 13′ levels to probe the local rearrangements at the hydrophobic girdle. Fig. S3 shows a representative experiment for non-α residues at 12′ (Fig. S3 a) and 13′ (Fig. S3 b). Interaction energies for paired substitutions at 12′T/S and V13′ are given in Tables S4 and S5, respectively. The order of average Δ²G₀ values between neighboring βδ-subunits was = 13′ > 9′ > 12′. Fig. 3 f represents a global view of all the experimental A–A coupling energies at 9′, 12′, and 13′, with the interaction strength depicted as the thickness of lines joining the vertices. It shows that there is an asymmetry in function between the non-α subunits at the gate.

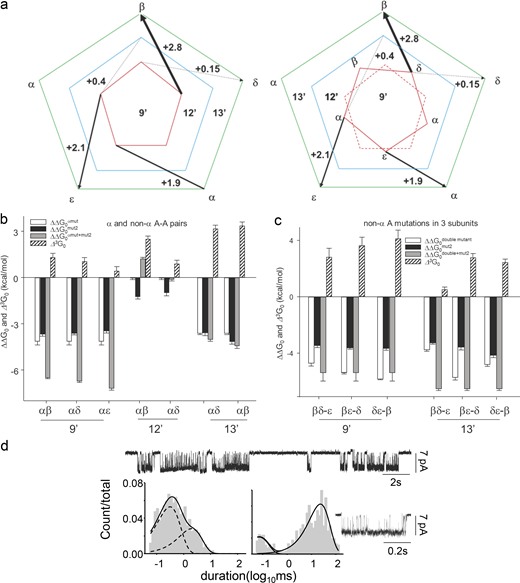
In a related LGIC, an outward “blooming” movement of the M2 pore helices has been implicated in the channel opening process (Martin et al., 2017). It was proposed that 9′ and 13′ side chains of adjacent subunits interact with each other during channel opening (Purohit et al., 2013). We will refer to these positions as complement pairs. To measure the strength of the interaction between neighboring 9′ and 13′ positions, we performed MCA. The interaction energy between δL9′ and βV13′ was +2.8 kcal mol⁻¹ (Fig. 4 a). As a negative control, we measured the interaction energy between the non-neighboring δV13′ and βL9′ pairs, which was only 0.15 kcal mol⁻¹ (Fig. 4 a). Interaction energies of all the complement pairs of residues are shown in Fig. 4 a (left) and Table S6. Fig. 4 a (right) shows an anti-clockwise rotation of 9′ residues relative to 13′.

To understand the interaction of non-α with the α subunits, we measured higher-order interaction energies (ΔⁿG₀). For example, we measured Δ³G₀ between αβ-, αδ-, and αε-subunits (2 α and 1 non-α subunit) at 9′ and 13′ positions at the gate. Fig. 4 b; and Tables S3, S4, and S5 show the Δ³G₀ values for αβ, αδ, αε-subunits at positions 9′, 12′, and 13′. Interaction between the α and non-α subunits at 13′ and 9′ positions (Ala) were 3.1 ± 0.4 and 0.9 ± 0.25 kcal mol⁻¹, respectively. Interaction at 12′T/S was negligible. However, interactions measured between non-α subunits (Fig. 4 c) at 13′ and 9′ positions were 1.1 ± 0.4 and 3.5 ± 0.6 kcal mol⁻¹, respectively. The interaction energies between non-α subunits at 12′ were not measured. It appears that α and neighboring non-α interactions at the 13′ position determine the hydrophobic energy barrier at the gate.

Then, we completely perturbed the gate by mutating all five subunits at 9′ and 13′ and measured the ΔΔG₀ at the gate. With Ala mutations at 13′, the total ΔΔG₀ was −11.4 kcal mol⁻¹ (Fig. 4 d; and Tables S3 and S5), with an estimated coupling energy of +3.3 kcal mol⁻¹. With Thr substitutions at 9′ in all five subunits, the ΔΔG₀ = −6.7 kcal mol⁻¹ with a total coupling energy of approximately +3.4 kcal mol⁻¹. In comparison, in the presence of ACh at both agonist sites, the O state is stabilized by −10.2 kcal mol⁻¹ (ΔΔG₂) relative to the C-state (Purohit and Auerbach, 2009; Nayak et al., 2012). It suggests that perturbing the hydrophobic gate stabilizes the O state of the apo receptors to levels comparable with that of the fully saturated liganded AChRs.

The functional change from a non-conducting to an ion-conducting channel requires many residues throughout the protein to undergo local rearrangements, from a C to an O conformation. These rearrangements are asynchronous on a sub-μs time scale. In AChRs activated by agonists, at least five groups of contiguous amino acids (a.k.a. “phi [ϕ] blocks”) sequentially undergo local C↔O transitions, starting at the TBS and ending at the gate. This cascade of domain rearrangements has been called a “conformational wave” (Grosman et al., 2000; Purohit and Auerbach, 2007). This pattern was deduced from experimental ϕ values of residues, which provide information about the relative time of local side chain rearrangements along the C↔O reaction coordinate (Auerbach, 2010). Moreover, because there is limited energy coupling between distant side chains, ϕ-analysis allows the sequential rearrangements to be localized to the receptor domains. In diliganded AChRs, ϕ values of amino acid residues at the gate are 0.1 ≤ ϕ ≤ 0.33 (Cymes et al, 2002; Purohit et al, 2013), indicating that these side chains undergo their local C→O transitions toward the end of the global channel-opening process, after the rearrangement of the ECD and most of the TMD.

ϕ Values of pore residues have not been measured in unliganded gating, so it is not known if they follow a similar conformational cascade in the absence of any ligand. We estimated ϕ values of gate residues from rate-equilibrium free-energy relationships (REFERs). A REFER is a log–log plot of the change in the forward (channel opening) rate constant versus the gating equilibrium constant for a series of mutations of one amino acid (see Materials and methods). The slope of a REFER plot is called ϕ. Fig. 5 shows the unliganded REFER plots for different amino acids at the gate. The average ϕ value of the gate region in the absence of agonists is 0.56 ± 0.08, which is significantly greater than the corresponding average liganded ϕ value. The shift to higher ϕ without agonists is likely caused by a shift of the transition state to a later position in the opening reaction sequence rather than by an alteration of the cascade sequence (Grosman, 2003).

To map the free-energy landscape in the pore during ionic flux in AChRs, we performed well-tempered metadynamics (WT-MTD) simulations of AChRs using PDB IDs 7QKO, 7QL6, and 6UWZ structures. Fig. 6 a shows initial membrane-embedded systems prepared for the simulations for WT AChRs using 7QKO and 7QL6. Fig. S4 c shows the time evolution of Cα RMSDs over the transmembrane domain over the duration of equilibrium simulations. The converged PMF profiles (Fig. S4 a) obtained from WT-MTD simulations show a broad energy barrier in −5 ≤ z/Å ≤ 15 range, with peaks at ∼5 and 0 Å for WT-C and WT-O, respectively (Fig. 6 b). The amino acid residues corresponding to z-axis coordinates of 0, 5, and 10 Å are L9′, V13′, and L16′, respectively. For C and O, the heights of the energy barriers with respect to the extracellular aqueous environment were +22.5 and +7.5 kcal mol⁻¹, respectively. Concomitant with a high energy barrier in C, we observed complete exclusion of water molecules between L9′ and L16′ in the pore (Fig. 6 c; and Video 1). During the unbiased simulation run, a water molecule was rarely seen creeping along the wall of the pore across the barrier in the WT-C state (Video 1). The observation of a broad energy barrier between residues 9′ and 16′ strongly corroborated the free-energy measurements from experiments on the AChR gate residues. In the α-Btx bound channel structure, the region spanning 9′–16′ residues was completely devoid of water densities (Video 3). No water molecule could be seen crossing its pore throughout the observation duration, unlike the WT-C structure.

To explore the molecular interactions that underlie the permeation energy barrier at the gate, we performed in silico mutagenesis of L9′ to S that is implicated in CMS. We prepared three membrane-embedded systems by incorporating L9′S mutations in either one (β), two (2α), or three (β, δ, and ε) subunits simultaneously (Fig. S4 b) and calculated the corresponding PMFs (Fig. S4 a). The system details are summarized in Table S7. The barrier to Na⁺ ion permeation progressively diminished at 9′ position (z = 0 Å) with an increasing number of L9′S mutations (Fig. 6 b). The free energy barrier of ∼17 kcal mol⁻¹ in the closed state was reduced to +11, +5.9, and +4.0 kcal mol⁻¹ with one (β), two (2α), or three (β, δ, and ε) L9′S mutations, respectively. This decrease in the free energy barrier at 9′ residues is accompanied by a slight increase in the pore radius (Fig. S1 a) and a rise in water density (Fig. 6 d) with an increasing number of mutations. The gradual increase in water occupancy at the 9′ level and contraction in the hydrophobic region having incorporated mutations can be clearly visualized in Fig. 6 d. However, the hydrophobic constriction is maintained between 13′ and 16′ residues, even if the ion permeation barrier height is significantly reduced to ∼15.5 kcal mol⁻¹ with double (α₂L9′S) and triple (βδεL9′S) mutations (Fig. 6 b).

Ionic flux through the channel requires a continuous water column. Fig. 6 d shows time-averaged water density profiles (Å⁻³) in the pore from simulations of WT-C (7QKO) and -O (7QL6), and with the above-mentioned 9′ mutations. In WT-C, the water density was found to be nil between 9′ and 16′ residues (0 ≤ z/Å ≤ 10), which remained constant throughout the duration of the simulation (Fig. S5,). Water density progressively increased at 9′ (z = 0 Å) upon the incorporation of an increasing number of L to S mutations. However, the mutations at 9′ residues failed to break the hydrophobic barrier from 13′ to 16′ residues, albeit some transient events of a few water molecules crossing the barrier were observed quite frequently. The water density distribution agreed well with the snapshots of the channel pore having corresponding hydration states (Fig. 7 a). Consequent to these mutations, the dewetted hydrophobic constriction can be observed to be gradually shrinking because of hydration at 9′ positions. Further, the time-dependent water occupancy along the channel axis (Fig. 7 b) validates enhanced water intrusion probability at the 9′ level, contracting the hydrophobic region with every additional L to S mutation incorporated. In the WT-O structure, the channel pore was observed to be fully occupied with water (Fig. 7 a). However, we observed a stochastic fluctuating wetting–dewetting transition (ns duration) of the open channel pore (Fig. 7 b and Video 2). This wetting–dewetting pattern is also replicated in the time-averaged water number density, resulting in an underestimated water density along the pore axis as reported in Fig. 6 d.

To delineate the structural basis of the gating transition, we compared the average WT-C versus WT-O conformations obtained from MD simulations by superimposing their M2 α-helices. Fig. 7 c illustrates the synaptic and membrane views of these superimposed structures (WT-C [blue]; WT-O [silver]) highlighting the residue side chain positions at the different hydrophobic constrictions (9′, 13′, and 16′) in the gate region. The M2 α-helices in the WT-O structure depict an outward tilt and rotation such that the pore residue side chains initially projecting in the lumen of the pore in the WT-C structure move away and start pointing toward the neighboring subunit M2 helices. This movement of the hydrophobic side chains away from the pore results in the widening of the gate region to allow water flow and wetting of the pore in WT-O conformation. However, the rotation of these side chains is uneven and was observed to be maximum for 16′ residues, broadening the pore to a great extent as observed in the HOLE diagram (Fig. S1). The 16′ residues in WT-C conformations were originally observed to be protruding in the pore lumen the most, congesting the pore to the narrowest size. We also observed outward tilting of the M2 helices in the WT-O structure in comparison to the WT-C conformation above the gate region (Fig. 7 c (iv)), significantly contributing to the increment in pore size in the open conformation. In summary, the gate undergoes overall (1) rotations of 9′, 13′, and 16′ side chains and (2) outward tilting of the pore helices in WT-O versus WT-C during C→O transition.

The global channel-opening conformational cascade propagates from the TBS through the ECD and TMD to the M2 gate to open the channel and allow ion conduction (Purohit et al., 2007). Results presented here (see below)—gating free-energy changes associated with side-chain substitutions at the 9′, 13′, and 16′ positions, linear correlation between ΔΔG₀ versus ΔΔG^trans, an inverse correlation of interaction energy (Δ²G₀) with side-chain hydrophobicity, and a broad, but high energy barrier between 9′ and 16′ positions—all support a hydrophobic gating mechanism in neuromuscular AChRs.

Hydrophobicity scales have been used previously for the prediction of protein secondary structures associated with or embedded in the membranes (Simm et al., 2016). Recently, Rao et al. (2019) used a normalized hydrophobicity scale to predict the hydrophobic barrier in the pores of 200 ion channel proteins. Standard transfer energy of amino acids from an aqueous pore lumen to an “oily” hydrophobic membrane environment may provide insight into the conformational changes of hydrophobic side chains during channel opening transition. Linear correlation between ΔΔG^trans versus ΔΔG₀ values (Fig. 2 f and Fig. S2) for side chain substitutions at 9′, 13′, and 16′ positions suggest that C↔O gating free energy changes are steeply dependent on the hydrophobicity of the pore-lining residues of the gate. Since, ΔΔG₀ and the gating free energy barrier (ΔΔG^ǂ) are linked by a linear free energy relationship (LFER, the slope of which is phi or ϕ), the energy barrier to ion permeation may be attributed to side chain hydrophobicity (see below).

The gate residues are asymmetric insofar as the variable ΔΔG₀ values associated with their mutations (Table S3) and side-chain conformational changes observed during the C→O gating transition (Fig. 3 f and Fig. 7 c). Mutating all the five subunits simultaneously at 9′ and 13′ positions resulted in open channels with Po ∼1.0. These suggest that at the gate, the hydrophobic energy barrier is due to asymmetric contribution from each subunit, where individual amino acid mutation only increases the probability of channel opening. However, a concerted conformational change in all pore-forming helices is necessary for complete collapse of the hydrophobic barrier and ion conduction.

Water at the gate influences ΔG₀. Ligand binding, the global gating conformational change, and ion permeation are energy-linked stages of a single continuum that are connected as an extended, multistage LFER (Gupta et al., 2017; Indurthi and Auerbach, 2023). A constitutively open AChR has a fast agonist association rate (∼10¹⁰ s⁻¹) constant (Nayak and Auerbach, 2017), indicating that the unliganded neurotransmitter binding sites and gate are entangled in the global isomerization, the last step of which involves wetting of the girdle and ion conduction. The O to C transition starts with the dewetting of the pore to terminate conduction and ends with the imposition of an entry barrier at the neurotransmitter sites that slows agonist association. Given this obligatory linkage, the experimental free energy measurements presented here contain information about the free energy change associated with the wet ↔ dry transition of the gate.

In MD simulations, we directly observed a “broken water column” at the gate and progressive weakening of the hydrophobic barrier. With the increasing number of polar substitutions at L9′, the pore widened and water occupancy in the pore increased proportionately. The water intrusion probability showed greater fluctuation with the increasing number of L9′S mutations and in the open channel clear stochastic wetting–dewetting transitions were observed. This confirms that the channel pore shuttles between a hydrated and a dehydrated pore passing through multiple semi-hydrated states (Fig. 7 a). That, perhaps, manifests as sub-conductance states in AChRs (Auerbach and Sachs, 1983) and BK channels (Jia et al., 2018). It is possible that intracluster mode switching apparent in constitutive single-channel openings in the mutants (Fig. 2 a, bottom) can be attributed to stochastic fluctuations in the hydration states of the pore. This possibility will be explored later elsewhere.

The intermittent wetting–dewetting transition in open channel pores raises a pertinent question about real-time capillary evaporation of water at the AChR gate. This can be explored using a simple structural model of the pore between 9′ and 16′, the narrowest region of the pore. The architecture here can safely be assumed to be cylindrical, with a radius that changes from ∼2.0 to 4 Å in the C→O transition. The height of the cylinder can be approximated as the rise per residue in a classical α-helix, 1.5 Å. By approximating the volume of an H₂O molecule as 2.99 × 10⁻²³ cm³, it can be calculated that in the constricted pore, the water-occupancy probability increases from ∼0 in C to ∼0.55 in O. The enthalpy of vaporization of water is 9.68 kcal mol⁻¹ (the amount of heat utilized in the evaporation of 1 mol of water). By assuming the wetting–dewetting transition is a non-equilibrium process where entropic changes are negligible, the change in barrier height can be approximated as 21.8 kcal mol⁻¹ during the C→O transition. Hence, this calculation, which assumes capillary evaporation, is in good agreement with the observed barrier to ion conduction by MD simulations.

A linear correlation between liganded versus unliganded gating free energy changes for the mutations at the gate indicates that there was no evidence of any direct/indirect, long-range energy coupling between the side-chain residues of the gate and the TBS. However, some mutations of aromatic residues at the TBS eliminate partially or completely a population of O conformational state that has a prolonged lifetime in unliganded gating (Purohit and Auerbach, 2009; Mukhtasimova and Sine, 2018). A progressive and reversible conformational cascade that propagates between TBS and gate, perhaps along the Cα-backbone, therefore, remains a likely mechanism of communication over distance in AChRs (Grosman et al., 2000; Purohit and Auerbach, 2007; Gupta et al., 2017).

Locally, the intersubunit interaction at the gate was studied by measuring coupling energy values. Lower coupling energy (Δ²G₀) values for native WT or mutated hydrophobic amino acids indicate that neighboring residues are either energetically independent or interact minimally among themselves and/or with the environment. This may thermodynamically favor local dewetting of the gate. In contrast, higher Δ²G₀ values for substituted polar/acidic amino acid residues indicate stronger interaction with local water molecules, potentially favoring wetting transition.

Our coupling energy measurements indicate the following about the gate: (1) Δ²G₀ values between neighboring subunits are greater than the non-neighboring residues (Fig. 3 c). (2) The ε/γ-subunit, which is expressed in adult/embryonic AChRs, interacts the least with other subunits at the gate, seemingly almost decoupled during C↔O gating transition. (3) Δ²G₀ between the complement pairs is consistent with an anti-clockwise rotation during the channel opening transition (Fig. 4 a), as has been proposed in other LGICs (Martin et al., 2017). The anti-clockwise rotation and outward flipping of the gate residues observed in MD simulations corroborate the coupling energy studies. (4) Coupling between α and non-α residues was the largest at 13′ and negligible at 9′ (Fig. 4 b). It appears that in the channel opening process, local resettling (interaction with water and other neighboring residues) of the α-subunit side chains at 13′ precedes that at 9′, although this possibility needs further validation. In support, however, one of the two α9′ residues has a gating ϕ value of 0.0, placing its movement at the very end of the opening process, after that of V13′ (Mitra et al., 2005). These results regarding the gate are in accord with the idea of a conformational “wave” propagation during global allosteric transition.

In silico mutagenesis of L9′ lowered the free energy barrier by 6 (βL9′S), 11 (α2L9′S), and 13 kcal mol⁻¹ (βδεL9′S) with the progressive increase in the number of mutations. In simulations, the pore diameters at 9′ level progressively increased from C to O through partially open-pore conformation with the number of mutations (Fig. S1 a). Progressive increase in constitutive channel opening with pore mutations, therefore, may be ascribed to the decreasing free energy barrier and increasing pore diameter. In O, the pore diameter widens from ∼2.7 to 8.2 Å at the narrowest region (at 16′) and from ∼3.1 to 6.3 Å at 9′ position. A change of only 1 Å was shown to cause pore wetting (Rasaiah et al., 2008), so a dewetting → wetting transition in C→O in AChRs is highly likely. Structural dynamics and experimental interaction energy studies suggest that the increase in pore diameter is caused by outward tilting and rotation of the side chains, akin to the blooming movements (Martin et al., 2017; Fig. 7 c).

Ion permeation at the gate is regulated by a broad energy barrier at the hydrophobic girdle between 9′ and 16′ residues in the ion channel pore. During channel opening transition, the gate residues undergo outward anti-clockwise rotations that result in a reduction in local hydrophobicity and wetting of the gate that allows ion conduction. Mutations of the gate residues, including those which cause CMS, increase constitutive channel opening by decreasing the free energy barrier and increasing the pore diameter.

Data in the manuscript are available from the corresponding author upon reasonable request.

Crina M. Nimigean served as editor.

We are thankful to Prof. James Gomes for infrastructural support. We thank M. Teeling and M. Shero for lab management. M. Kumari thanks the UGC India for the research fellowship. The authors acknowledge IIT Delhi HPC facility for computational resources.

The research was funded by Science and Engineering Research Board (SERB) SRG (SRG/2019/001518) and SERB CRG (CRG/2022/007550) grant to T.K. Nayak.

Author contributions: Conceptualization: T.K. Nayak; execution of research, data analyses, and interpretation, review of manuscript: M. Kumari, N. Khatoon, R. Sharma, S. Adusumilli, H.K. Kashyap, and T.K. Nayak; original manuscript preparation: T.K. Nayak, H.K. Kashyap, and A. Auerbach.