Microtubules form by progressively faster tubulin accretion, not by nucleation–elongation

The microtubule cytoskeleton plays essential roles organizing the interior of eukaryotic cells. Microtubules can act as “tracks” for motor-based transport, form the basis of the mitotic spindle that mediates proper segregation of chromosomes during cell division, and help define cell polarization (Barlan and Gelfand, 2017; Desai and Mitchison, 1997; Prosser and Pelletier, 2017). To fulfill these many roles, microtubules must assemble into a multitude of highly dynamic and spatially diverse networks. The dynamic instability of microtubules (Mitchison and Kirschner, 1984), which describes the switching of individual polymers between phases of growing and shrinking, allows wholesale reorganization of the microtubule network to occur rapidly and also provides a mechanism to efficiently search space (Holy and Leibler, 1994). Indeed, numerous regulatory factors allow cells to control how fast microtubules grow and how frequently they switch from growing to shrinking (catastrophe) or from shrinking back to growing (rescue; Akhmanova and Steinmetz, 2015), as well as control the creation of new microtubules (Kollman et al., 2011; Roostalu and Surrey, 2017; Wieczorek et al., 2015), a process called nucleation.

Microtubules are hollow, cylindrical polymers formed from αβ-tubulin heterodimers that interact with each other in two ways: stronger head-to-tail (longitudinal) interactions between αβ-tubulins make up the straight protofilaments, and weaker side-to-side (lateral) interactions hold protofilaments together. The mechanisms underlying the dynamic instability of existing microtubules are increasingly well understood (Alushin et al., 2014; Driver et al., 2017; Duellberg et al., 2016; Gardner et al., 2011; Geyer et al., 2015; Grishchuk et al., 2005; Manka and Moores, 2018; Margolin et al., 2012; Piedra et al., 2016; VanBuren et al., 2005; VanBuren et al., 2002; Zhang et al., 2015), although fundamental aspects such as the structure of the growing end and how different conformations of αβ-tubulin affect the strength of polymerization contacts remain debated.

Models for how existing microtubules grow and shrink cannot specify how new microtubules form de novo, because a different balance of αβ-tubulin–αβ-tubulin contacts is required and because different conformations of αβ-tubulin are probably involved. Thus, our understanding of the mechanisms that govern spontaneous microtubule formation remains relatively primitive (reviewed in Roostalu and Surrey, 2017). Multiple factors contribute to this difficulty. First, nucleation occurs very rarely and cannot truly be observed microscopically, so measuring it directly is much harder than measuring the growing and shrinking of existing microtubules. Second, the open, tube-like structure of the microtubule poses unique complications. In most organisms, microtubules contain 13 protofilaments, although there are clear examples of specialized microtubules containing 11 or 15 protofilaments (Burton et al., 1975; Chaaban et al., 2018; Chalfie and Thomson, 1982; Davis and Gull, 1983; Kwiatkowska et al., 2006; Saito and Hama, 1982; Tucker et al., 1992). Regardless of protofilament number, the hollow nature of the microtubule means that it takes many more αβ-tubulin subunits to close a tube than it does to make a minimal helical repeat for a simpler, helical polymer like actin. Perhaps not surprisingly, given this complexity, there is no consensus about the sequence of intermediates that must be formed (pathway) during the transition from individual subunits to a closed tube. To further complicate matters, the structure of the αβ-tubulin heterodimer also changes during assembly, from a bent confirmation in solution to a straight conformation within the final microtubule (Ayaz et al., 2012; Nawrotek et al., 2011; Rice et al., 2008; reviewed in Brouhard and Rice, 2018). Where in the assembly process the straightening takes place, whether it is continuous or stepwise, how much energy is required, and how this obligatory conformational change affects nucleation all remain unknown. In addition to these factors, the GTPase activity required for microtubule catastrophe can also antagonize nucleation by destabilizing intermediate species.

An early study of the kinetics of spontaneous microtubule nucleation, which used solution conditions that suppress catastrophe to simplify the behavior, posited that nucleation proceeded sequentially through two discrete intermediates (Voter and Erickson, 1984). The data were reanalyzed in later studies (Flyvbjerg et al., 1996; Flyvbjerg et al., 1995) that proposed a more complex pathway containing four distinct nucleation intermediates (6-mer, 9-mer, 12-mer, and 15-mer of αβ-tubulin). However, despite the substantial appeal of the phenomenological analysis used in this later study, it was not possible to ascribe a biochemical interpretation to the species or rate constants (Flyvbjerg et al., 1996). In different work, cross-linked αβ-tubulin oligomers were used to arrive at the conclusion that there was a degenerate set of pathways underlying spontaneous microtubule assembly, but in that work, it was again difficult to gain insight into the underlying biochemistry (Caudron et al., 2002), highlighting the challenges to understand microtubule nucleation. Thus, the physical/chemical details of the underlying assembly process continue to remain obscure.

In this work, we sought to obtain more explicit insight into the molecular mechanisms that govern spontaneous microtubule assembly. Our primary goal was to explore the simplest biochemical models that could faithfully explain the experimental data. We began from the fundamental modes of αβ-tubulin interactions within a microtubule: a single subunit (heterodimer) can make a longitudinal interaction, a lateral interaction, or both simultaneously (corner interaction). Starting with explicit simulations of the biochemical reactions that can occur for all possible αβ-tubulin oligomers up to 12-mers, we observed that a small subset of all possible oligomers became dominant. These dominant oligomers were rectangular, meaning that they maximized the number of longitudinal and lateral contacts such that there were no unfilled corners. The dominance of a small subset of species allowed us to develop a simpler, approximate model based almost exclusively on rectangular oligomers. This simplification allowed the model to access arbitrarily large oligomers in a way that retained a connection to the fundamental biochemical interaction modes of the individual subunits.

This approximate but biochemically faithful minimal model provides a new way to view microtubule nucleation. Rather than proceeding via a distinct rare, rate-limiting “nucleus” as in classical nucleation–elongation models, our model indicates that microtubule assembly involves the continuous accretion of αβ-tubulins into a growing 2D lattice. Like crystallization processes, the larger the assembly, the faster it grows. Our minimal model reveals assembly pathways for forming a new microtubule and provides new insights into how exogeneous nucleators and other regulatory factors can accelerate microtubule formation.

To obtain biochemical insight into possible pathways for spontaneous microtubule assembly, we constructed an explicit model that includes all nonredundant tubulin oligomers from dimers through dodecamers (Fig. 1 A shows the intermediates through hexamers). Here, nonredundant means that we only consider a single exemplar n-mer for each unique combination of longitudinal and lateral contacts; statistical weighting of rate constants ensures that this exemplar oligomer faithfully represents the ensemble of species it represents (see example in Fig. S1 A). We defined the biochemical pathways that connect different oligomers (arrows in Fig. 1 A) by assuming that oligomers grow and shrink via addition and loss of individual αβ-tubulin subunits. It was not practical to explore larger oligomers in this formulation because of an explosion in the number of species and reactions (reaching dodecamers requires ∼200 distinct species and ∼600 reactions; Fig. 1 F).

We implemented the differential equations describing this discrete assembly scheme in Berkeley Madonna (Marcoline et al., 2020) to simulate the assembly pathway and kinetics. The only free parameters in this model are the on-rate constant k_f and the affinities for the three different αβ-tubulin interaction modes (longitudinal, lateral, and corner [simultaneous longitudinal + lateral interaction]; Fig. 1 D). Note that because of avidity, the corner affinity is expected to be substantially stronger than the product of longitudinal and lateral affinities (Erickson and Pantaloni, 1981). As is common, k_f was assumed (here, we chose 10⁶ M⁻¹s⁻¹ based on experimental observations and consistent with work from others; Coombes et al., 2013; Margolin et al., 2012; McIntosh et al., 2018; VanBuren et al., 2002; Zakharov et al., 2015). We explored different values for the three parameters, seeking to identify conditions under which some appreciable concentration of dodecamers would form. We were especially interested in the corner affinity, because this is the interaction that would provide the driving force for microtubule elongation. A relatively tight corner affinity (K_d^corner < 0.2 µM; Fig. S1, B–D) was required for appreciable flux into the largest oligomers. With high-affinity corner interactions, the simulations predominantly populated a small number of rectangular oligomers, defined as oligomers wherein (1) every subunit makes at least one longitudinal and one lateral contact to another, and (2) there are no “open” corner sites (Fig. 1 B). More explicitly, what happens in the simulations is that formation of an initial 2 × 2 oligomer forms relatively quickly. The next larger species containing an additional “singleton” tubulin are poorly populated because of the weak longitudinal and lateral affinities, but those species also present an open, high-affinity corner site. Filling this open site stabilizes the first subunit and in the case of a 2 × 2 start fills the next longitudinal or lateral layer, resulting in a 3 × 2 or 2 × 3 assembly, respectively. On larger assemblies, additional corners are vacant after the first, and these fill rapidly, essentially “zipping up” the layer. The net consequence is that once initiated, layer completion occurs efficiently, explaining why rectangular species dominate.

Only considering rectangular oligomers greatly reduces the number of species and reactions required to reach much larger oligomers in simulations (e.g., Fig. 1, C and F). However, in such an approximation, the rates of adding or losing a layer become context dependent and depend on the height and width of the oligomer. Indeed, the importance of rectangular oligomers was recognized some time ago (Erickson and Pantaloni, 1981), but at that time, it was not practical to develop a kinetic model to simulate assembly time courses. Using the steady-state approximation, we were able to derive a general recursive expression for the effective “forward” rate of adding of a longitudinal or lateral layer (see Materials and methods). An example of adding a longitudinal layer to a 2 × 2 oligomer is illustrated in Fig. 1 D. Considering the layer addition as a sequence of individual steps also allowed us to derive an effective forward rate as well as a layer equilibrium ratio, which describes the expected relative populations of oligomers that differ by a single layer (Materials and methods). Importantly, in these expressions, both the forward rate and equilibrium ratio for layer addition are defined in terms of the biochemical properties of individual subunits (longitudinal, lateral, and corner affinities/rates). Consequently, and in contrast to what occurs with phenomenological models, the reduction in the number of species and reactions does not come at the expense of losing a connection to the fundamental biochemical behavior. For the 12-mer simulated explicitly above, the layer model provides a >10-fold reduction in species and >35-fold reduction in number of reactions (Fig. 1 F; these reduction factors increase dramatically for larger oligomer sizes).

We implemented the reduced, layer-based model into Berkeley Madonna to test if it could recapitulate the results from our explicit simulations when using the same input parameters for subunit affinities. Despite the dramatic reduction in complexity, and with the exception of very-low-abundance intermediate species, the simplified layer-based simulations quantitatively reproduced the oligomer concentrations and the kinetics of oligomer formation observed with the explicit model (compare Fig. 1 E to Fig. 1 B). These initial benchmarking layer simulations only considered oligomers up to dodecamers so that we could make a direct comparison with the explicit model. In the next section, we expand the model to include the much larger oligomers required to depict microtubule assembly.

We wrote a custom program to expand the layer model to arbitrary sized rectangular oligomers. Whenever an oligomer gained a 13th protofilament, we converted it into a microtubule. No additional penalty for seam formation was included. We assumed that once formed, microtubules elongate by capturing αβ-tubulin subunits one at a time, consistent with the linear dependence of microtubule elongation rate on concentration This assumption allowed us to model elongation without having to explicitly represent the configuration of microtubule ends or make assumptions about the mechanism of elongation. To minimize the number of adjustable parameters, and because we do not explicitly model detailed end configurations, the same rate constants were used for events at either the plus or minus ends (the elongation rate in our model effectively represents the sum of plus- and minus-end elongation rates). These additional simplifying assumptions allow the model to simulate spontaneous microtubule assembly and the ensuing depletion of free αβ-tubulin subunits in a relatively natural way, without having to explicitly specify a particular nucleus, assume a particular assembly pathway, or make decisions about microtubule end configurations.

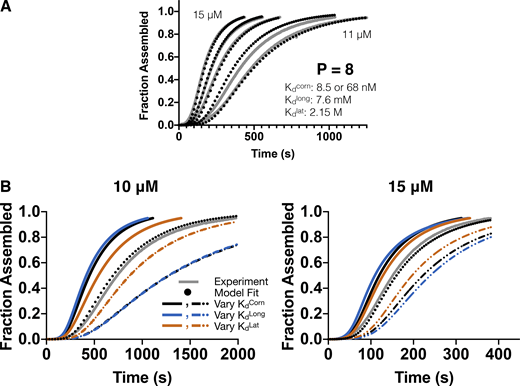
We began testing our model by fitting it to experimental assembly curves that we measured by light scattering (Fig. 2 A). The model was able to fit individual curves quite well (Fig. 2 B), with minor discrepancies evident at low concentration. The optimized affinities differed somewhat from fit to fit but shared common features: tight corner affinities (K_d^corn < 100 nM), weaker longitudinal affinities (K_d^long ∼5–15 mM), and lateral affinities ∼10-fold weaker than longitudinal affinities (Fig. 2 B). The longitudinal affinity we obtained is in the range of that obtained from biochemical models for microtubule growing and shrinking (e.g., Gardner et al., 2011; Kim and Rice, 2019; Piedra et al., 2016; VanBuren et al., 2002). The corner and lateral affinities are both ∼10-fold stronger than in those models, a difference that might reflect the different buffer conditions (high glycerol concentration) in nucleation assays relative to dynamics assays. The corner affinity is much stronger than the product of longitudinal and lateral affinities, which may seem counterintuitive but actually is expected because of avidity. The individual longitudinal and lateral affinities represent a balance between (among other things) favorable protein–protein contacts and the unfavorable entropic cost of losing rotational and translational degrees of freedom; when making a corner interaction, the summed favorable contribution from both longitudinal and lateral interfaces more greatly outweighs the entropic cost, such that the corner affinity can be much higher (this concept is explained in detail in Erickson and Pantaloni, 1981). Fits to an independent set of assembly curves (Fig. S2 A) yielded similar affinities (Fig. S2 B). We found it encouraging that the model could fit individual assembly curves, but to be convincing, a single parameter set should be able to fit all the assembly curves simultaneously. Thus, we turned to global fitting, where we attempted to fit the set of assembly curves with one common parameter set.

In a global fit to the set of assembly curves (Fig. 2 C), a limitation of the model became apparent; even though each individual concentration could be well fit (Fig. 2 B), the model could not capture the correct behavior over the broad concentration range measured (Fig. 2 C). The model appeared to fit the alternative dataset somewhat better (Fig. S2 C), although an outlier curve also limited the concentration range available for fitting. The net rate of microtubule elongation predicted from these parameters is ∼1 µm/min at 13 µM αβ-tubulin, which is comparable to but slightly lower than the plus- and minus-end elongation rates of 1.5 µm/min and 0.4 µm/min, respectively (combined growth rate of 1.9 µm/min), observed in a recent study (Strothman et al., 2019; note also that the presence of glycerol in our assay is expected to reduce microtubule elongation rates compared with standard, glycerol-free buffers; Molines et al., 2020). More importantly, the overall concentration dependence of the assembly curves was still being underestimated. Because all layer transition rates scale with the chosen on-rate constant (see derivations in Materials and methods), changing the assumed on-rate does not improve the global fits.

The observed discrepancy between model and experiment suggests that the model fails to capture some important aspect of assembly. In reexamining our assumptions, we realized that it was too restrictive to consider only monomer addition and loss as the “elemental” reactions within the layer assembly pathway. Indeed, a simple calculation demonstrates that any model having these relative lateral and longitudinal affinities must also include a “dimer pathway” (Fig. 2 D). Compared with the "two-step" monomer-based pathway in which a first monomer associates weakly and only becomes “locked in” by a subsequent corner association (Fig. 2 D, middle path), when the longitudinal affinity is stronger than the lateral one as it is for microtubules it is more efficient to initiate a lateral layer by adding a preformed longitudinal dimer (Fig. 2 D, lower path; see also Materials and methods and Fig. S3). This is true even though longitudinal dimers are present at very low concentrations (roughly 1 part in 1,000 or ∼10 nM) for the parameters we used. Our “monomer-only” model global fit required a longitudinal affinity ∼10-fold stronger than the lateral one, but under those conditions, additions of longitudinal dimers should actually account for ∼90% of the lateral layer initiations (Fig. 2 E). Thus, despite appearing reasonable, the fits do not make biochemical sense, because the model fails to account for a dimer pathway that has the potential to dominate the flux through oligomers. It has been suggested that oligomer associations may be important during spontaneous microtubule assembly (Erickson and Pantaloni, 1981; Mozziconacci et al., 2008; Voter and Erickson, 1984), but to our knowledge, these interactions have not previously been implemented into kinetic models. Also, without a biochemical model, it is difficult to determine the relative importance of different oligomer reactions.

The cartoons and calculations presented in Fig. 2, D and E illustrate how the rate of initiating a new lateral layer will depend on the concentration of longitudinal dimers of αβ-tubulin. By contrast, once the slow step of initiating a new layer has occurred, zipping up via addition into favorable corner (longitudinal + lateral) sites should occur almost exclusively via αβ-tubulin monomers, because these monomers far exceed longitudinal dimers in number/concentration. By a similar logic, it is also not necessary to include a dimer pathway for initiating a longitudinal layer; lateral dimers are very rare, and the upper αβ-tubulin of a longitudinal dimer provides no increased stabilization as a longitudinal layer builds up.

Incorporating a parallel, dimer-based pathway for initiating lateral layers (Fig. S3) requires that at each step we specify (1) the concentration of longitudinal dimers, (2) an association rate constant for the longitudinal dimers adding to a complete layer, and (3) a dissociation rate constant for the lateral “unbinding” of a longitudinal dimer. The concentration of longitudinal dimers is easily calculated given the concentration of monomers and the equilibrium constant for longitudinal interactions. Because off-rate constants tend to vary over a much larger range than on-rate constants, for simplicity, we used the same, roughly diffusion limited association rate constant as we do for monomers. We derived a formula that expresses the equilibrium constant for lateral association of a longitudinal dimer solely in terms of biochemical properties of the monomers (see Materials and methods). Thus, we were able to parameterize the “dimer pathway” purely in terms of the fundamental monomer properties.

We first fit the dimer model to individual assembly curves, as we did for the monomer model (Fig. 3 A). The longitudinal and corner affinities for these dimer model fits were comparable to those obtained from fits of the monomer model. The lateral affinity (∼25–30 M in the dimer model) was ∼300-fold weaker than the in the monomer model (∼100 mM), reflecting a greatly diminished contribution of the monomer pathway for lateral initiation. Although it was predicted to be required biochemically, including this dimer pathway actually degraded the ability of the model to recapitulate the shape of individual assembly curves compared with the monomer-only fits; the simulated assembly curves displayed a less pronounced lag phase and also appeared less cooperative (shallower sigmoid transition; compare Fig. 3 A to Fig. 2 B). This demonstrates how changing the relative rates of longitudinal and lateral accretion alters the shape and concentration dependence of the assembly curves. Global fits of the dimer model to the set of assembly curves were also markedly poorer than for the monomer model (Fig. 3 B). Thus, a more complete biochemical model for the assembly process paradoxically degraded its predictive power.

Why was the monomer-only model able to fit the observed assembly curves so much better than a model incorporating a dimer pathway? The presence of a dimer pathway makes the effective rates of lateral and longitudinal growth much more comparable to each other (Fig. 2 D, compare top and bottom rate expressions), whereas in the monomer-only model, there is significantly more contrast between the rates for longitudinal and lateral growth. We speculated that the otherwise more accurate monomer + dimer model must still be missing a critical feature that acts to increase the difference between longitudinal and lateral growth.

What might be missing? Not having accounted for the effects of conformational changes in αβ-tubulin that occur during microtubule formation (Ayaz et al., 2012; Nawrotek et al., 2011; Pecqueur et al., 2012; Wang and Nogales, 2005) is a strong candidate. Indeed, it is now well established that unpolymerized αβ-tubulin subunits adopt a curved conformation in solution and that the microtubule lattice itself acts as an allosteric activator to straighten αβ-tubulin during the assembly process (Ayaz et al., 2012; Buey et al., 2006; Nawrotek et al., 2011; Rice et al., 2008). That is, αβ-tubulin becomes progressively straighter as it becomes increasingly surrounded by lateral neighbors (reviewed in Brouhard and Rice, 2018; Fig. 4 A). This straightening-induced conformational strain acts to weaken lateral interactions in assemblies that require more straightening. To explore these ideas in the context of our model, we introduced a very simple lateral penalty to mimic the greater strain intrinsic to straighter conformations. We assumed that two-wide assemblies could remain curved, whereas wider assemblies would be forced to straighten, making the lateral interactions after the first pairing in a given “row” X-fold weaker.

We fit the monomer + dimer + penalty model to the data as before, testing a range of penalty magnitudes (from 1 to 16 in Fig. 4 B). The global fit to the experimental curves improved as the magnitude of the lateral penalty increased, with the best fits reached for penalty values greater than 4. Thus, penalizing lateral growth was sufficient to “correct” the deficiencies of the simple dimer pathway, resulting in even better fits (Fig. 4, B and C; penalty value = 8) than for the monomer-only model (see Fig. 3, B and C). Beyond a value of 4, the improvement in global fit only weakly depends on the precise value of the penalty (Fig. 4 B). Fits to the alternative dataset yielded similar, but not identical, affinities (Fig. S4 A and Table S1). Other penalty factors gave fits of comparable quality as long as the penalty factor was greater than 4 (Fig. 4 B) but yielded different longitudinal and lateral affinities, as expected. Varying individual parameters shows that the fits are sensitive to small (1.5-fold) changes in the parameter values (Fig. S4, B and C). Differences in the fitted parameters for the primary and alternative dataset suggests that within a narrow range, there may be some compensation between corner and longitudinal affinities (compare Fig. 4 C to Fig. S4 A). We did not attempt to add a penalty to the monomer model, because even if doing so improves the quality of fit to the data, a monomer + penalty model would not make physical sense; mass action considerations would still dictate that dimer associations must play a substantial role whenever longitudinal affinity is higher than lateral affinity. Collectively, our computational experiments led us to what we believe to be the first simple, biochemically based model that can accurately recapitulate the observed concentration-dependent kinetics of spontaneous microtubule assembly without having to assume a specific nucleus.

The model developed here provides a biochemical pathway that explains in a new way why the kinetics of microtubule initiation are slow relative to polymer elongation. As a first way to illustrate the assembly pathway that emerges from fitting our model to the experimental data, we plotted the total concentration and average size of intermediate oligomers as a function of time (Fig. 5 A). The total concentration of oligomers peaks at ∼200 s in the example shown, and the subsequent decrease is a consequence of the formation of microtubules and the depletion of free αβ-tubulin. The average oligomer size increases gradually over several hundred seconds, reflecting the slow process of accretion and the low likelihood that large layers will be lost in “backward” reactions.

The endpoint of microtubule formation (closure of the cylindrical lattice) requires a minimal-width oligomer (13 in our model). There is a clear lag time before an appreciable concentration of microtubules can be formed (Fig. 5 B) such that the maximal rate of microtubule formation does not occur at the onset of the reaction. This delay and associated rate evolution reflects the slow process of accretion and that makes the kinetics of spontaneous microtubule formation so different from simpler polymers that show classical nucleation–elongation behavior wherein the critical nucleus is in a rapid equilibrium with unpolymerized subunits. To provide insight into the nature of the assembly pathway, we next examined the summed concentration of tubulin oligomers with a given width (lateral extent) as a function of time (Fig. 5 C). This analysis shows that the concentration of oligomers decreases as their width increases (e.g., there are fewer three-wide oligomers than two-wide and fewer four-wide oligomers than three-wide; Fig. 5 C). This decreasing concentration of wider oligomers happens because the transition from one width to the next accelerates throughout the assembly process. This acceleration can be understood as a statistical/kinetic consequence of the 2D assembly pathway. No matter their height, all oligomers of a given width grow taller with the same characteristic rate because they present the same number of “landing sites” for starting a new longitudinal layer. However, taller oligomers grow wider faster than shorter oligomers, because their increased height provides more landing sites for starting a new lateral layer. Similarly, wider oligomers add longitudinal layers faster than the narrower ones for the same reason.

To provide more granular insight into the nature of the predominant microtubule assembly intermediates, we examined the distribution of oligomer sizes at different widths (Fig. 5 D). For each oligomer width, and at the time the concentration of oligomers of that width peaked, we plotted the most populated height (filled circle) and the relative amount of taller or shorter oligomers (gray teardrop/oval shapes, which are actually a set of circles with area scaled proportionally to the concentration). The many parallel pathways in the assembly process leads to an increasing spread in the range of oligomer heights as they get wider. For example, the most populated 50% of all 3-wide oligomers have heights between 7 and 11 (a height range of 5), whereas the most populated 50% of all 12-wide oligomers span heights between 50 and 64 (a height range of 15, three times greater than for 3-wide oligomers). The most populated immediate microtubule precursor (12 subunits wide) contains almost 700 tubulins: 58 subunits tall × 12 wide. This is much larger than the number of subunits in the nucleus predicted by phenomenological models (Flyvbjerg et al., 1996; Flyvbjerg et al., 1995). Also note that the rate of layer assembly cannot exceed the rate of elongation. The layer-based assembly model thus provides a new, ensemble-based view of the assembly pathway wherein many oligomers of varying heights contribute appreciably to the formation of new microtubules.

How existing microtubules grow and shrink is increasingly well understood, but even for this well-studied process, fundamental aspects remain debated. It is well appreciated that αβ-tubulin changes conformation when associating with the microtubule end, but there is little quantitative insight into how the different conformations of αβ-tubulin affect the strength of lateral and longitudinal interfaces. Similarly, while it is well established that the GDP state of the microtubule is substantially destabilized relative to the GTP state, a definitive understanding of the mechanism by which GTP stabilizes tubulin–tubulin contacts in the microtubule remains lacking. These and other ambiguities in the quantitative understanding of microtubule growing and shrinking may explain why different groups using different kinds of models arrive at very different estimates of the strength of different tubulin–tubulin interactions.

The understanding of how new microtubules form spontaneously (a related but mechanistically distinct process from the growing and shrinking of existing microtubules) lags far behind (Roostalu and Surrey, 2017). Many discussions of spontaneous microtubule formation have invoked the concept of a “critical nucleus,” which is analogous to the transition state of a chemical reaction (Kollman et al., 2011; Flyvbjerg et al., 1995; Roostalu and Surrey, 2017; Voter and Erickson, 1984). This traditional view of the assembly pathway assumes that (1) the formation and growth of early intermediates is thermodynamically unfavorable, and (2) above a critical size, oligomer growth by monomer addition becomes favorable, and this elongation proceeds at a fixed rate. The polymerization kinetics of relatively simple helical polymers like actin can be well described by two-step, nucleation–elongation models that invoke a small critical nucleus representing a mini-filament (the smallest oligomeric species that presents helical binding sites; Sept and McCammon, 2001; Tobacman and Korn, 1983). However, the spontaneous assembly kinetics of hollow, cylindrical microtubules show steeper than quadratic time dependence early in the reactions (Flyvbjerg et al., 1996; Flyvbjerg et al., 1995; Voter and Erickson, 1984); this behavior cannot arise in a classical two-step nucleation–elongation mechanism. Phenomenological mechanisms that invoke multiple, sequential nucleation intermediates (Flyvbjerg et al., 1996) can fit microtubule assembly curves but fail to provide biochemical insights into the assembly pathway.

Our model provides an alternative and conceptually distinct framework for thinking about the pathway for microtubule formation (Fig. 6) and the biochemical factors that govern the overall rate of assembly. From this comes the understanding that there is not a singular, transition-state-like species (variously estimated as 8–27 tubulins) that dictates the assembly kinetics, but instead, what we would traditionally call “nucleation” arises from an ensemble of accretion events involving many species and hundreds of tubulin heterodimers, with the smallest species dominating the kinetics. Some prior studies have provided evidence for sheet-like intermediates (Mozziconacci et al., 2008; Portran et al., 2017; Voter and Erickson, 1984; Wang et al., 2005), although it has been challenging to detect and quantify the concentration of these intermediates. In what follows, we summarize the main features of the predicted assembly pathway and discuss implications for the multiple ways that a template or other regulatory factor could accelerate the process.

The layer growth model predicts that a multitude of pathways and intermediates contribute meaningfully to microtubule assembly. High-affinity corner interactions lead to the dominance of rectangular species, and longitudinal interactions being stronger than lateral ones causes the preferred rectangular intermediates to be taller than they are wide. Stronger longitudinal compared with lateral affinity also has the consequence that initiation of lateral accretion will be dominated by associations of longitudinal dimers of αβ-tubulins. Early in the assembly pathway, transitions to larger oligomers become energetically favorable (equilibrium ratio less than one) but still occur slowly, because the oligomers are small and initiating the new layer depends on a weak individual longitudinal or lateral interaction. The rate of transition between oligomers accelerates as oligomers increase in size not because of any intrinsic changes in the underlying affinities but because larger oligomers present more sites from which the next layer can initiate. These size-dependent changes in transition rates are a direct consequence of the 2D nature of the assembly pathway. Thus, even though nearly all of the layer additions are energetically “downhill,” the repeated difficulty of initiating each new layer contributes a series of progressively smaller delays into the assembly sequence that in combination represent the effective “barrier.” Conformational straightening of αβ-tubulins adds an additional kind of frustration that makes lateral growth of early oligomers even harder. Collectively, the ensemble of initiation barriers creates a kind of “frustration” that dictates unique kinetics for spontaneous microtubule assembly.

This layer-based view of the assembly pathway provides new ways for thinking about how regulatory factors might accelerate microtubule initiation. Our modeling indicates that the kinetics of microtubule formation are dictated by the need for repeated “layer” transitions that are limited by the weaker lateral affinity and the straightening penalty (e.g., Fig. 7 A). Classical nucleators like the γ-tubulin ring complex (γ-TuRC; Zheng et al., 1995) contain a lateral array of 14 γ-tubulins (Fig. 7 B) that are thought to form a template on which a microtubule can elongate (Consolati et al., 2020; Kollman et al., 2015; Kollman et al., 2011; Liu et al., 2020; Moritz et al., 1995; Wieczorek et al., 2020). We used our model to explore how the potency of templating might depend on the width of the template. We modified our simulations to include various width templating oligomers (Fig. 7 C) using a constant total amount of templating monomers. Note that in these simulations, there are progressively lower concentrations of the wider oligomers (e.g., half as many four-wide oligomers as two-wide). The affinity of αβ-tubulins for γ-TuRC is unknown, so we explored a regimen where γ–αβ longitudinal interactions are identical to αβ–αβ interactions and another where γ–αβ longitudinal interactions are weaker than αβ–αβ interactions (Fig. 7). With the stronger γ–αβ interaction strength, even two-wide templates potently accelerated assembly (not shown). This is at odds with experimental data showing that γ-tubulin small complexes (γ-TuSCs), which only contain two γ-tubulins, are much poorer nucleators than γ-TuRCs (Kollman et al., 2015; Oegema et al., 1999). By contrast, when γ–αβ interactions were assumed to be weaker than αβ–αβ interactions, templating oligomers that were two subunits wide only modestly accelerated the predicted assembly kinetics (1.1-fold faster characteristic time for assembly [T_0.1]; Fig. 7, C and D). A three-wide oligomer was much more potent (1.7-fold faster), even though in the simulations, the concentration of three-wide oligomers was less than that of the two-wide oligomer. This strong change in potency occurs because the “hardest” transition in the assembly sequence is from two-wide oligomers to three-wide oligomers, providing an explanation for why γ-tubulin small complexes (γ-TuSCs) only weakly stimulate assembly (Oegema et al., 1999). In our simulations, progressively wider templating arrays show even greater potency, emphasizing that the barriers to lateral growth contribute throughout the entire assembly pathway.

The idea that multiple reactions/transitions contribute to limit the overall rate of microtubule formation also suggests that strategies besides templating could enhance the rate of spontaneous assembly. The rates for layer additions depend on how fast tubulins “land” on the growing sheet, so enhancing this rate should promote layer initiation and zippering. For example, XMAP215 family polymerases use an “accelerated delivery” mechanism (Ayaz et al., 2014; Geyer et al., 2018) to make microtubules grow faster, and this same activity likely underlies the role for XMAP215 family proteins in microtubule nucleation (Gunzelmann et al., 2018; King et al., 2020; Popov et al., 2002; Roostalu et al., 2015; Thawani et al., 2018; Wieczorek et al., 2015). The efficiency of initiating new layers is primarily limited by the relatively weak longitudinal or lateral affinities, especially for the singleton tubulin that initiates each longitudinal layer. Thus, a factor that stabilizes these associations should also increase the rate at which layer transitions occur. Proteins like TPX2 and doublecortin bridge between neighboring subunits in the lattice (Fourniol et al., 2010; Zhang et al., 2017); this “molecular stapling” may help explain their documented roles in microtubule nucleation (Moores et al., 2004; Roostalu et al., 2015). Finally, altering the allosteric properties of αβ-tubulin itself should also profoundly affect microtubule initiation. For example, and in keeping with predictions of our model, studies of an αβ-tubulin conformation cycle mutation (Geyer et al., 2015) that enhances the strength of lateral interactions (Driver et al., 2017; perhaps via reducing the cost of αβ-tubulin straightening) greatly accelerates microtubule formation. Similarly, small-molecule compounds like Taxol that stimulate microtubule initiation and growth may do so by promoting straightening, relieving that additional barrier.

We described a minimal accretion model that explains spontaneous microtubule assembly kinetics in terms of subunit biochemistry and an ensemble of rectangular intermediates. Whereas in typical nucleation–elongation paradigms the scarcity of the transition-state-like nucleus is what limits the rate of polymer formation, our model is more akin to a process like crystal growth. Indeed, in our accretion model most of the steps toward polymer formation are energetically favorable but kinetically frustrated by the difficulty of initiating new layers; this difficulty decreases as layers become larger, because more landing opportunities are presented. We do not yet understand quantitatively how the ensemble of accretion events and interface affinities together dictate phenomenological aspects of the assembly curves like the overall concentration dependence of the reaction rate or the time dependence of assembly at early times, but it nevertheless seems clear that the accretion mechanism we describe is a direct consequence of the 2D nature of the hollow, cylindrical microtubule lattice.

We did not consider the kinetic consequences of GTP hydrolysis within the nascent polymer in our model, because it was not possible to account for the stochastic hydrolysis within the context of our deterministic formalism. In keeping with that, our assay conditions included high concentrations of glycerol to suppress microtubule catastrophe. We attempted to measure assembly curves in the presence of Guanosine-5'-[(α,β)-methyleno]triphosphate (GMPCPP), a hydrolysis-resistant GTP analogue, but obtained variable results because it was difficult to reliably eliminate contaminating amounts of microtubule seeds from the initial reaction mixtures. Ignoring GTPase activity and using glycerol to suppress catastrophe represent limitations of our model that we plan to address in future work. In general terms, GTPase activity should antagonize assembly by destabilizing intermediate oligomers, but because different conformations of αβ-tubulin may be involved at different stages of assembly, the effects of GTPase may not be evenly distributed across all oligomers. Likewise, the presence of glycerol likely alters the propensities for oligomer formation. Thus, the affinities we report may underestimate the true affinities. Because we sought to develop a minimal model, we did not adjust association rates depending on neighbor context, as has been done for microtubule elongation (Castle and Odde, 2013). However, these context-dependent effects are unlikely to make large contributions to spontaneous assembly; transitions between the smallest intermediates contribute most to the overall rate in our accretion model, and the small size of those intermediates means that they present a simpler distribution of open sites compared with a microtubule end. Thus, even though we made these and other simplifying assumptions, we still expect that growth through accretion will represent the dominant pathway for assembly.

Finally, our model provides a unifying quantitative framework for understanding the complex effects of regulatory molecules. Indeed, the zippering transitions between rectangular oligomers that dominate the initiation process also share many features in common with microtubule elongation. Thus, our model also explains why factors that regulate microtubule elongation and shrinking also regulate spontaneous microtubule assembly.

The spontaneous assembly of phosphocellulose-purified porcine-brain tubulin was followed by turbidity at 350 nm basically as described previously (Gaskin et al., 1974; Voter and Erickson, 1984). Care was taken to remove microtubule seeds and inactive protein by cycling it through an additional polymerization/depolymerization step just before use; immediately before performing assays, tubulin at −80°C was rapidly thawed at 37°C and placed on an ice-water slurry (0°C), and the buffer was adjusted to 80 mM K-Pipes, pH 6.8, 1 mM EGTA, 4 mM MgCl₂, and 1 mM GTP. After 5-min incubation, 0.5 vol of 37°C glycerol was mixed in, and the tubulin was allowed to polymerize at 37°C for 20 min. Microtubules were pelleted through a 37°C, 60% glycerol cushion in 50 mM K-MES, pH 6.6, 5 mM MgSO₄, 1 mM EGTA, and 1 mM GTP in a TLA110 rotor (Beckman) at 80,000 rpm for 20 min. The pellets were resuspended at 37°C in assembly buffer (50 mM K-MES, pH 6.6, 3.4 M glycerol, 5 mM MgSO₄, 1 mM EGTA, and 1 mM GTP) using a warm Potter homogenizer. The resuspended microtubules were then depolymerized on an ice-water slurry for 20 min and centrifuged in a TLA100.3 rotor at 100,000 rpm for 35 min at 2°C to remove any remaining polymerized tubulin. The supernatant from this cold spin was removed and used for the assembly reactions. The tubulin was kept at 0°C as reaction mixtures were prepared. A series of samples was prepared at different tubulin concentrations in assembly buffer and kept at 0°C in thin-walled, 0.5-ml plastic tubes (PCR tubes; Stratagene). Samples were rapidly heated to 37°C directly in cuvettes prewarmed to 37°C in a Pelltier cell changer (took 30 s) in a custom-built spectrophotometer. The absorbance at 350 nm was recorded approximately every 4 s on four samples at a time until plateaus were reached. Recording on the spectrometer was started before transfer of tubulin to the cuvettes so that early lag-phase data were not missed. The time was adjusted to ignore the 30-s heating step.

We constructed a model in Berkeley Madonna (Marcoline et al., 2020) to simulate αβ-tubulin self-assembly. The first step in this process was to define the set of αβ-tubulin oligomers and how they are related to each other by gain/loss of an αβ-tubulin though a longitudinal, lateral, or longitudinal + lateral (corner) interaction. Starting from the 2D nature of the microtubule lattice, we built a list of all possible configurations for an αβ-tubulin oligomer of a given size. Fig. 1 A illustrates how there are two kinds of possible dimers of αβ-tubulin (longitudinal and lateral), three kinds of trimers of αβ-tubulin, etc. Larger oligomers can have multiple configurations that are energetically equivalent. To minimize the number of species and reactions considered in the model, we used a single exemplar species to represent each set of n-mers with the same number of longitudinal and lateral contacts. For each exemplar species, population-weighted average rate constants were used to account for the different properties of each oligomer. Fig. S1 A provides a worked example of this approximation for a tetramer of αβ-tubulin. We then used the Chemical Reactions module in Berkeley Madonna (Marcoline et al., 2020) to build a set of rate equations corresponding to each possible transition. We did not pursue oligomers larger than 12-mers, because the number of species and reactions became intractable. This model provides a way to analyze the rate and extent to which different species become populated for a given choice of the adjustable parameters.

The explicit, monomer-based simulations in Berkeley Madonna (Marcoline et al., 2020) indicated that a simpler reaction scheme that only considered transitions between rectangular oligomers. We used the steady-state approximation to derive effective rate constants for these transitions, as described below.

To determine if this reduced representation could accurately recapitulate the time courses for rectangular species in the explicit model, we constructed a new model in Berkeley Madonna (Marcoline et al., 2020; also truncated at 12-mers) that considered monomer-based reactions to form the first rectangular intermediate, a 2 × 2 tetramer of αβ-tubulin, but that only considered layer transitions for larger species (Fig. 1 C), using the layer rate laws described above. We input expressions for the layer transition rates as derived above and ran the simulations using the same biochemical parameters used in the explicit simulations. The layer model faithfully reproduced the results from the explicit simulations (Fig. 1).

To enable simulations of arbitrarily large oligomers, we wrote a custom computer program that effectively performs the same calculations of Berkeley Madonna but in a more automated way that makes it easier to incorporate a much larger number of species and reactions. The program automates the generation of the list of possible rectangular oligomers [(2,2), (3,2), (2,3), etc.] and the recursive calculation of rate constants for transitions between them (as explained above and in Fig. S5). The program then integrates the set of transition rate laws using finite-difference methods. At each time point, the program uses longitudinal and lateral affinities along with the concentration of “free” tubulin (here, free means the population not incorporated into rectangular oligomers (2,2) or larger) to calculate the concentration of free tubulin monomers and longitudinal and lateral dimers and trimers, assuming these species are all in rapid equilibrium (see box in Fig. 1 E); using these quantities, the program then takes a small step forward in time, updating quantities of all rectangular oligomers according to the rate laws and the layer rate constants. This results in an updated set of concentrations for the rectangular oligomers (and hence of free tubulin), and the process is repeated. To account for microtubule formation, we simply converted species that became 13 protofilaments wide into microtubules, and we assumed that microtubules elongated by monomer addition with a rate that depends linearly on tubulin concentration, as has been observed in experiments. We did not explicitly consider the seam or the variable configuration of the microtubule end, and for simplicity, we assumed plus and minus ends elongated with identical kinetics. Effectively, ignoring the differences between microtubule ends means that the net rate of microtubule elongation in our model represents the sum of elongation rates at plus and minus ends. The expression we used to obtain the net rate of elongation, 2 × (k_f[αβ] − k_r^Corner), gives realistic elongation rates (see main text), was chosen purely for convenience and does not imply any assumptions about configurations of the microtubule ends. We used a downhill simplex algorithm to fit the simulated time courses to the experimental ones using fraction of tubulin in rectangular oligomers as a proxy for the normalized assembly data.

To investigate the effects of template-like nucleators in the model, we modified the simulations to include an additional template species. We assumed a constant total concentration of monomers that were distributed into templating oligomers of different widths. This assumption means that progressively wider oligomers are present in the simulations at progressively lower concentrations; for example, for a given concentration of templating monomers, there will be half as many four-wide oligomers as two-wide, and so on. For calculating the rate constants for the first layer addition onto the template, we assumed that only one longitudinal interface of this templating oligomer (the plus end) was active for nucleation.

In initial runs wherein interactions between γ- and αβ-tubulin were assumed to be of identical affinity, we observed potent nucleation even from templates that were only two subunits wide. Because two-wide nucleators like the γ-TuSC are much less potent than 12- to 14-wide oligomers like the γ-TuRC (Kollman et al., 2015; Oegema et al., 1999), we also performed simulations with 10-fold weaker interactions between γ- and αβ-tubulin than for αβ–αβ interactions (Fig. 7).

Fig. S1 illustrates aspects of the explicit self-association model, the concept of nonredundant oligomers and how oligomer concentrations depend on the adjustable parameters. Fig. S2 shows fits to a second dataset. Fig. S3 provides illustration of the dimer pathway and how it affects later transition rate constants. Fig. S4 shows fits of the dimer + penalty model to the alternate dataset along and how model predictions change with variation in the model parameters. Fig. S5 provides illustrations to help explain how weighting factors for the layer model were derived. Table S1 summarizes fits of the best model to the two datasets.

We thank T. Davis and her colleagues for critical feedback on a prior version of the manuscript and J. Cleary for helpful discussions.

This study was supported by the National Science Foundation (grants MCB-2017687, MCB-1615938, and MCB-1054947 to L.M. Rice) and the National Institutes of Health (grants R01 GM031627, R35 GM118099, and P01 GM105537 to D.A. Agard). D.A. Agard was supported in part by the Howard Hughes Medical Institute.

The authors declare no competing financial interests.

Author contributions: M. Moritz collected the microtubule assembly data and helped write the manuscript. L.M. Rice constructed models, fit the data, and drafted the manuscript. D.A. Agard analyzed data, supervised the research, and helped write the manuscript.