Agonist molecules at the two neuromuscular acetylcholine (ACh) receptor (AChR) transmitter-binding sites increase the probability of channel opening. In one hypothesis for AChR activation (“priming”), the capping of loop C at each binding site transfers energy independently to the distant gate over a discrete structural pathway. We used single-channel analyses to examine the experimental support for this proposal with regard to brief unliganded openings, the effects of loop-C modifications, the effects of mutations to residues either on or off the putative pathway, and state models for describing currents at low [ACh]. The results show that (a) diliganded and brief unliganded openings are generated by the same essential, global transition; (b) the radical manipulation of loop C does not prevent channel opening but impairs agonist binding; (c) both on- and off-pathway mutations alter gating by changing the relative stability of the open-channel conformation by local interactions rather than by perturbing a specific site–gate communication link; and (d) it is possible to estimate directly the rate constants for agonist dissociation from and association to both the low and high affinity forms of the AChR-binding site by using a cyclic kinetic model. We conclude that the mechanism of energy transfer between the binding sites and the gate remains an open question.
INTRODUCTION
Nicotinic acetylcholine (ACh) receptors (AChRs) are ligand-gated ion channels that mediate fast chemical communication at the vertebrate neuromuscular synapse. These membrane proteins switch between two native conformational ensembles that have a C(losed) or an O(pen) channel, either with or without ligands present at two transmitter-binding sites (Auerbach, 2013). When agonists are present at the binding sites, the open-channel probability (Po) increases simply because these ligands bind with higher affinity to O versus C. In AChRs, the end states of the global C↔O allosteric transition (“gating”) have different enthalpies and entropies (Gupta and Auerbach, 2011), which suggests changes in both structure and dynamics (Tsai et al., 2008). Note that we use the word “gating” to refer to the full allosteric transition of the pentamer and not just the microscopic step of this complex process that results in a conductance change of the pore.
The adult neuromuscular AChR is a pentamer comprised of four different but homologous subunits (α2βδε). The two transmitter-binding sites are in the extracellular domain (ECD) ∼5 nm from each other and from the gate region in the transmembrane domain (TMD) (Fig. 1 A). Each transmitter-binding site is comprised of three loops in the principal α subunit and one in the complementary ε/δ subunit (Fig. 1 B). In the ACh-binding protein (AChBP), a soluble homologue of the AChR ECD, α-subunit loop C is flexible and shows an inward displacement (“capping”) when certain ligands are present (Celie et al., 2004; Hansen et al., 2005; Brams et al., 2011). A similar rearrangement of loop C has been observed in Torpedo marmorata AChRs, although the movement may be more restricted than in AChBP (Unwin and Fujiyoshi, 2012).
The two transmitter-binding sites have different complementary subunits and, hence, different structural elements. However, in adult-type mouse AChRs, the two sites happen to be functionally equivalent, with each having approximately the same affinity for ACh regardless of whether the protein is in the resting-C or active-O conformation (Jha and Auerbach, 2010). When the protein switches from C to O, each binding site increases its affinity for ACh by a factor of ∼6,000 (from ∼170 to ∼0.03 µM). This event increases the C↔O gating equilibrium constant by a factor of ∼36 million (stabilizes O relative to C by approximately −10 kcal/mol) and the single-channel Po from ∼10−6 in the absence of ligands to ∼0.96 with two bound neurotransmitters.
The increase in affinity for the agonist is just one of several intermediate events within the C→O arrow (Grosman et al., 2000; Lape et al., 2008). The gating equilibrium constants (O vs. C free energy differences) we report reflect the product (sum) of those of the microscopic transitions between all of the intermediates states that comprise the full protein allosteric transition, which includes both the affinity change for the agonist and the conductance change of the pore.
Loop-C capping has been proposed to initiate AChR channel opening (Karlin, 1969; Celie et al., 2004). This idea has emerged mainly from a comparison of the relative position of loop C in AChBPs with versus without bound ligands. For ∼40 different ligands, there is a correlation between the degree of capping and the action of ligand on AChR function, with agonists showing more contracted conformations and antagonists showing more extended conformations (Brams et al., 2011). However, other experiments suggest that loop C is mainly involved in forming favorable contacts with the ligand, in both the low and high affinity conformations of the binding site (Jadey and Auerbach, 2012). In this view, loop-C capping could increase the open-channel probability not by transferring energy over distance but simply by increasing the relative stability of the open-channel conformation through local interactions at the binding site.
Several hypotheses have been put forward for the mechanism that links the binding sites and the gate. Single-channel kinetic (phi-value) analyses suggest that the protein is divided into microdomains that each undergo a local C↔O rearrangement (Auerbach, 2005). In this model, neighboring domains interact and isomerize sequentially to generate a “Brownian conformational wave” connecting the binding sites and the gate, with residues in the binding site loops moving near the onset of channel opening. Elastic network models show that the protein’s breathing motions may be able to bring about a global “quaternary twist” that opens/closes the pore (Taly et al., 2005). In this mechanism, the gating conformational change is generated by the concerted motions of the entire pentamer backbone. These models also suggest that loop-C motion occurs relatively early in channel opening (Zheng and Auerbach, 2011). In the “priming” hypothesis, the binding sites and the gate communicate by sequential movements of a discrete set of primary and secondary structural elements (Mukhtasimova et al., 2009). In this mechanism, each binding site reversibly communicates with the gate by structural changes along a defined pathway and does so independently of the other binding site. Again, loop-C capping is proposed to occur at the onset of channel opening.
Many years ago, a “stepwise” model for AChR gating was proposed in which binding energy from the affinity change moves independently from each site to the gate, with rapid opening occurring only after both sites have contributed (Auerbach, 1992). The experimental evidence for independent energy transfer from each binding site was only from single-channel kinetics. The standard sequential-state model for describing AChR binding and gating by agonists is A↔AC↔A2C↔A2O, where A is the agonist (the Del Castillo and Katz [1957] model). Models with an added, brief AC′ state interposed between AC and A2C provided a better fit to the current interval durations. AC′ was interpreted as a state in which energy from only one of two low→high affinity–binding events had appeared at the gate (Auerbach, 1993).
The priming model extends and offers new experimental support for this idea as well as a specific structural path for site–gate communication (Mukhtasimova et al., 2009). In this hypothesis, the capping motion of each C loop independently transfers energy toward the gate via specific β strands in the ECD and residues at the ECD–TMD interface (Lee and Sine, 2005; Lee et al., 2008; Mukhtasimova et al., 2009). The proposed sequence of gating rearrangements (loop C→β9–10→interface→M2→gate; Lee et al., 2009) is appealing because it occurs over a contiguous set of structural elements (Fig. 1 A). The evidence presented in support of this hypothesis was from analyses of single-channel currents from WT, mutant, and cysteine cross-linked AChRs, recorded both in the absence and presence of agonists.
Here, we examine the experimental foundations of the priming model for site–gate communication in AChRs. We show that loop-C capping is not a necessary trigger for channel opening.
MATERIALS AND METHODS
Cell culture and mutagenesis
Human embryonic kidney (HEK) 293 cells were maintained in Dulbecco’s minimal essential medium supplemented with 10% fetal bovine serum and 1% penicillin–streptomycin, pH 7.4. The cultures were incubated at 37°C and 5% CO2. The QuikChange site-directed mutagenesis kit (Agilent Technologies) was used to create mutations or deletions that were verified by nucleotide sequencing. HEK cells were transiently transfected using the calcium phosphate precipitation method by incubating them for ∼15 h with 3.5–5.5 µg DNA per 35-mm culture dish in the ratio of 2:1:1:1 (α/β/δ/ε). The cells were cotransfected with GFP (0.1 µg/µl\e) as a marker protein. Cells were washed by changing the media after ∼15 h of transfection, and electrophysiological recordings were made within ∼36 h after washing. All constructs expressed well except for those with glycine substitutions in loop C.
Electrophysiology
Single-channel currents were recorded in the cell-attached patch configuration at room temperature. The composition of the bath solution was as follows (mM): 142 KCl, 5.4 NaCl, 1.8 CaCl2, 1.7 MgCl2, and 10 HEPES/KOH, pH 7.4. The patch pipettes were filled with Dulbecco’s phosphate-buffered saline containing (mM): 137 NaCl, 0.9 CaCl2, 2.7 KCl, 1.5 KH2PO4, 0.5 MgCl2, and 8.1 Na2HPO4, pH 7.3 NaOH. For the experiments with agonists, ACh was added only to the pipette solution. Stock ACh solution was diluted to the desired concentration using Dulbecco’s phosphate-buffered saline. Patch pipettes (∼10-MΩ) were fabricated from borosilicate glass and coated with sylgard (Dow Corning). Single-channel currents were acquired using an amplifier (PC505B; Warner instruments), low-pass filtered at 20 kHz using an external filter (LPF-8; Warner instruments), and digitized at a sampling frequency of 50 kHz using a data acquisition board (SCB-68; National Instruments). The wire and pipette holder used in unliganded studies were never exposed to agonists.
Kinetic modeling
Kinetic analysis of single-channel data was performed by using QUB software. For estimation of the rate constants, clusters of openings flanked by greater than or equal to ∼20-ms silent periods were selected by eye. Currents within clusters were idealized into noise-free intervals after further digital low-pass filtering at 12–15 kHz by using the segmental k-means algorithm (Qin, 2004). The forward (fn, where n is the number of bound agonists) and backward (bn) gating rate constants were estimated from the idealized interval durations by using a maximum-interval likelihood algorithm after imposing a dead time of 25 µs (Qin et al., 1997). The unliganded gating equilibrium constant was calculated from the ratio of the rate constants, E0 = f0/b0.
The idealized intracluster interval durations were fitted by Markov state models. For all of the binding site mutants, the unliganded open- and closed-interval durations were described by a simple two-state model (C↔O). With WT-binding sites, additional C and O states were added, one at a time, until the log-likelihood score failed to improve by >10 units. The rate constants f0 and b0 were computed as the inverse of the predominant closed- and open-lifetime components.
The data shown in Fig. 5 were fitted by three different four-state schemes (Table 4). Two of the schemes were linear (O↔C↔AC↔AO and C↔O↔AO↔AC) and had six free parameters. Detailed balance was enforced in the full cyclic scheme, which had seven free parameters.
In the presence of saturating concentrations of agonist, the fully resolved gating intervals can be well described by a two-state model, either A2C↔A2O (with agonists) or C↔O (without agonists and a mutation of a core aromatic). However, there are short-lived intermediate states between the stable closed- and open-channel conformations (Lape et al., 2008). In our experiments, the brief sojourns in these states were not resolved as discrete events, so the forward and backward “gating” rate constants pertain to the complete passage between the ground states. Sojourns in intermediate gating states do not influence the energy difference between C and O (log of the gating equilibrium constant) estimated by using a two-state model. These experimentally determined values reflect the sum of the energy changes (product of the equilibrium constants) for all of the steps through whatever sequence of intermediate states may exist. Here, we are only concerned with the total C↔O equilibrium constant (“gating”) and not with the separation of this quantity into its factors.
RESULTS
Unliganded openings
In the absence of agonists, WT AChRs rarely open (Jackson, 1986), but many mutations increase substantially the level of constitutive activity (Purohit and Auerbach, 2009). The mutations need not be at the binding sites, ECD–TMD interface, or gate, but they can be in many different places throughout the protein. Fig. 2 shows examples of unliganded single-channel currents from mouse AChRs having the same mutations used in the experiments to support the priming model in human AChRs (βδM2-9′S, in the gate region of the pore; see Fig. 1 A) (Purohit and Auerbach, 2009; Nayak et al., 2012).
AChR and AChBP structures. (A) Torpedo AChR α and δ subunits (Protein Data Bank accession no. 2bg9; Unwin, 2005). ECD, extracellular domain; TMD, transmembrane domain. Horizontal lines mark approximately the membrane. Purple, loop C; blue,β9–10; green, ECD–TMD interface; tan, αM2. Spheres, on-pathway residues (gray) αW149 (binding site), αP272 (M2–M3 linker), and αL251 (M2-9’ gate region), and off-pathway residues (white) δP123 (loop D; aligns with εP121) and αA96 (loop A) (see Fig. 4). (B) Close-up view of the Lymnaea stagnalis AChBP ligand-binding site (Protein Data Bank accession no. 1uv6; Celie et al., 2004). White, primary subunit (α in AChRs); tan, complementary subunit (ε or δ in AChRs); green, the four core aromatic residues (AChR numbering); ligand, carbamylcholine. Spheres, αC atoms of the terminal residues of loop C (αV188 and αY198 in mouse AChRs).
AChR and AChBP structures. (A) Torpedo AChR α and δ subunits (Protein Data Bank accession no. 2bg9; Unwin, 2005). ECD, extracellular domain; TMD, transmembrane domain. Horizontal lines mark approximately the membrane. Purple, loop C; blue,β9–10; green, ECD–TMD interface; tan, αM2. Spheres, on-pathway residues (gray) αW149 (binding site), αP272 (M2–M3 linker), and αL251 (M2-9’ gate region), and off-pathway residues (white) δP123 (loop D; aligns with εP121) and αA96 (loop A) (see Fig. 4). (B) Close-up view of the Lymnaea stagnalis AChBP ligand-binding site (Protein Data Bank accession no. 1uv6; Celie et al., 2004). White, primary subunit (α in AChRs); tan, complementary subunit (ε or δ in AChRs); green, the four core aromatic residues (AChR numbering); ligand, carbamylcholine. Spheres, αC atoms of the terminal residues of loop C (αV188 and αY198 in mouse AChRs).
As has been known many years, without agonists the gating of unliganded AChRs is not described by a simple two-state C↔O scheme (Jackson, 1986; Grosman and Auerbach, 2000). Most unliganded openings are brief, but a few are long-lived. The two populations of unliganded openings can be seen easily in current traces and in the intracluster interval duration histograms that have multiple open components (Fig. 2, A and B). In AChRs with WT-binding sites, long openings are present in βδ9′S and in ∼100 other, different constructs having background mutation(s) that increases constitutive activity (for example, Purohit and Auerbach, 2009; Nayak et al., 2012).
Mutation of a core aromatic eliminates the long component of unliganded openings. (A; top) Single-channel openings from unliganded, constitutively active AChRs occur in clusters (open is down). The shut periods between clusters are times when all AChRs in the patch are desensitized. The background mutations were at the gate region (βδM2-9′S); the binding sites were WT. (Bottom) Patch open-interval duration histogram and example cluster show both brief and long openings. (B) Example clusters and open-interval duration histograms from AChRs having WT-binding sites plus different background mutations that increase the level of constitutive activity. Both brief and long openings are apparent. (C) Phe mutations of the core aromatic amino acids (Fig. 1 B) eliminate long openings but leave the brief ones nearly unchanged (see A for the activity with only background mutations present). Almost all mutations of these four residues, and only these, abolish long openings.
Mutation of a core aromatic eliminates the long component of unliganded openings. (A; top) Single-channel openings from unliganded, constitutively active AChRs occur in clusters (open is down). The shut periods between clusters are times when all AChRs in the patch are desensitized. The background mutations were at the gate region (βδM2-9′S); the binding sites were WT. (Bottom) Patch open-interval duration histogram and example cluster show both brief and long openings. (B) Example clusters and open-interval duration histograms from AChRs having WT-binding sites plus different background mutations that increase the level of constitutive activity. Both brief and long openings are apparent. (C) Phe mutations of the core aromatic amino acids (Fig. 1 B) eliminate long openings but leave the brief ones nearly unchanged (see A for the activity with only background mutations present). Almost all mutations of these four residues, and only these, abolish long openings.
The priming proposal makes an important assumption regarding the two populations of unliganded openings: activation of only one binding site generates brief openings, and activation of two sites generates long openings. The proposal is that without agonists, the brief openings arise from AChRs in which only one C loop has capped to perturb just one of the two α-subunit ECD–TMD interfaces (“singly primed”), and that long openings reflect AChRs in which such rearrangements have occurred in both α subunits (“doubly primed”). In this view, brief unliganded openings arise from AChRs in which only a portion of the overall gating transition has occurred.
The α-subunit side of each binding site has four core aromatic residues (Fig. 1 B). Fig. 2 C shows examples of unliganded gating activity in AChRs having a Phe mutation at just one of these residues (at both binding sites) in addition to the distant βδ9′S background mutations. In all of these constructs, constitutive gating activity without agonists did not have both brief and long openings but was well described by a simple C↔O model. Moreover, the spontaneous activity from these AChRs was similar to the brief openings observed in AChRs having WT-binding sites. A Phe substitution of any one of the core aromatics (at both binding sites) eliminated the long openings but hardly affected the brief ones. One of these aromatic mutations (αY190F) was studied using the same background mutations in human AChRs, and again only brief events persisted (Mukhtasimova et al., 2009).
Previously, the effects of ∼50 different substitutions of the core aromatics were examined using a variety of constitutively active background constructs (Purohit and Auerbach, 2010). As was the case with the Phe substitutions and the βδ9′S background, almost all (96%) of the aromatic mutations eliminated the long component but left the brief one nearly unchanged. There appears to be nothing special about loop-C residue αY190 or Phe substitutions with regard to their ability to eliminate long openings, or about the βδ9′S mutation with regard to its ability to elicit long openings when the binding sites are WT.
According to the priming hypothesis, these observations indicate that the mutation of a core aromatic at both binding sites eliminates site–gate energy transfer, but only at one of the two binding sites. That is, removing the hydroxyl group from αY198 (in both α subunits) prevents priming from the α–ε (for example) binding site but not from α–δ. This is unexpected but possible.
The priming speculation is that the brief openings that remain after the aromatic mutation arise from AChRs in which only a single α subunit undergoes a C↔O conformational change. However, the properties of these brief openings are in many respects the same as those for diliganded gating events in which both α subunits undergo a C↔O conformational change (Purohit and Auerbach, 2009; Nayak et al., 2012). The open intervals have the same conductance (72 vs. 67 pS). The gating equilibrium constants have the same voltage dependence (58 vs. 61 mV/e-fold change) and change approximately to the same extent with the addition of distant background mutations (Table 3). For example, the mutation αS269I (in αM2; Fig. 4) increases the brief unliganded gating equilibrium constant by ∼90-fold and the diliganded gating equilibrium constant by ∼115-fold. The shut- and open-interval lifetimes also respond quantitatively to mutations in approximately the same way, as phi values for six different residues (in the α, δ, and ε subunits) are the same for brief unliganded and diliganded gating. These results suggest that brief unliganded and diliganded gating events occur by the same essential, global conformational change.
Further support for this hypothesis comes from a consideration of the intrinsic energy of gating, which is the O versus C free energy difference in the absence of agonists. In the presence of agonists, the A2C versus A2O energy difference is the sum of the unliganded O versus C energy difference and the binding energy from the agonist arising from the low→high affinity change at the two binding sites (Purohit et al., 2012; Auerbach, 2013). The unliganded gating energy has been estimated from the properties of just brief openings (+8.3 kcal/mol; Purohit and Auerbach, 2009). According to the priming model, this is the intrinsic energy of the isomerization of just one α subunit. This energy has also been estimated from diliganded gating where both subunits have isomerized (+8.5 kcal/mol; Jha and Auerbach, 2010). That the two estimates are the same implies that diliganded and brief unliganded openings are generated by the same essential, global C↔O transition, and that brief openings do not reflect AChRs having only one activated α subunit.
Loop C
A second component of the priming model is that each priming event results from transition of a C loop from the uncapped to the capped conformation. Other results suggest that loop C is mainly involved with agonist binding (Jadey and Auerbach, 2012). To further explore the role of loop C in binding versus gating, we examined several loop-C deletion/substitution constructs, both without and with agonists present.
We modified loop C (in both α subunits) by altering the 11-residue region between α188 and α198 (mouse sequence VFYSCCPTTPY; Fig. 1 A). The first tyrosine in this sequence is αY190, an amino acid that is particularly important for both low affinity binding and the low-to-high affinity transition that increases the gating equilibrium constant (Tomaselli et al., 1991; Chen et al., 1995). We replaced the 11 loop-C residues with n = 11, 9, 7, 5, or 3 glycines and used background mutations to increase the level of constitutive activity.
Fig. 3 A shows example unliganded clusters from AChR having a WT (top) or modified C loop. Gating in all of these highly modified loop-C constructs was approximately the same as in the background construct. That is, the unliganded gating rate and equilibrium constants, and the extent to which these constants changed with the addition of a background mutation, were similar to those of the unliganded brief component in AChRs having two WT C loops (Tables 1 and 2). In these loop-C constructs, the long component of unliganded openings was absent. Loop C contains two of the four core aromatics (αY190 and αY198), so the absence of the long component is consistent with the observation that all four of these residues must be WT for long openings to be present.
Loop-C capping increases channel opening by increasing agonist binding and not by a long-distance energy transfer. The 11 loop-C residues (Fig. 1 B) were replaced by n = 11, 9, 7, 5, or 3 glycines. (A) Gating in the absence of ligands; the background mutations increased constitutive gating but had no effect on agonist binding (αA96H in loop A and εS450W in M4). Left, the residues in loop C (V188 to Y198); middle, open-interval duration histograms; right, example currents. (Top) WT loop C. Constructs with modified C loops produce unliganded gating activity having similar properties as the WT (Table 1). Progressive replacement with glycines hardly changes the brief component of unliganded gating, which is normal even when loop C has been deleted. (B) Activation by ACh. (Top) The 11-glycine construct was not activated by 1,000 µM ACh (compare with the 11-gly trace in A). (Bottom) With tyrosines at positions αY190 and αY198 (9-gly/2-tyr), ACh increases the open probability within clusters, indicating that the agonist can bind and increase the gating equilibrium constant (concentration in micrometer given above each trace). (C) Two point mutations in loop B of the binding site mimic the effects of loop-C cross-linking (no agonist added).
Loop-C capping increases channel opening by increasing agonist binding and not by a long-distance energy transfer. The 11 loop-C residues (Fig. 1 B) were replaced by n = 11, 9, 7, 5, or 3 glycines. (A) Gating in the absence of ligands; the background mutations increased constitutive gating but had no effect on agonist binding (αA96H in loop A and εS450W in M4). Left, the residues in loop C (V188 to Y198); middle, open-interval duration histograms; right, example currents. (Top) WT loop C. Constructs with modified C loops produce unliganded gating activity having similar properties as the WT (Table 1). Progressive replacement with glycines hardly changes the brief component of unliganded gating, which is normal even when loop C has been deleted. (B) Activation by ACh. (Top) The 11-glycine construct was not activated by 1,000 µM ACh (compare with the 11-gly trace in A). (Bottom) With tyrosines at positions αY190 and αY198 (9-gly/2-tyr), ACh increases the open probability within clusters, indicating that the agonist can bind and increase the gating equilibrium constant (concentration in micrometer given above each trace). (C) Two point mutations in loop B of the binding site mimic the effects of loop-C cross-linking (no agonist added).
Unliganded gating constants for loop-C glycine constructs
| Construct | f0 | ±SE | b0 | ±SE | E0 | ±SE | Emut/wt0 | n |
| WT loop C | 234 | 7 | 1,931 | 189 | 0.123 | 0.01 | — | 3 |
| 11gly | 438 | 24 | 2,536 | 151 | 0.173 | 0.01 | 1.4 | 3 |
| 9gly | 464 | 24 | 2,578 | 488 | 0.194 | 0.04 | 1.6 | 3 |
| 7gly | 547 | 62 | 2,314 | 612 | 0.281 | 0.09 | 2.3 | 3 |
| 5gly | 423 | 94 | 3,196 | 813 | 0.204 | 0.08 | 1.7 | 5 |
| 3gly | 464 | 58 | 1,877 | 18 | 0.246 | 0.03 | 2.0 | 3 |
| Construct | f0 | ±SE | b0 | ±SE | E0 | ±SE | Emut/wt0 | n |
| WT loop C | 234 | 7 | 1,931 | 189 | 0.123 | 0.01 | — | 3 |
| 11gly | 438 | 24 | 2,536 | 151 | 0.173 | 0.01 | 1.4 | 3 |
| 9gly | 464 | 24 | 2,578 | 488 | 0.194 | 0.04 | 1.6 | 3 |
| 7gly | 547 | 62 | 2,314 | 612 | 0.281 | 0.09 | 2.3 | 3 |
| 5gly | 423 | 94 | 3,196 | 813 | 0.204 | 0.08 | 1.7 | 5 |
| 3gly | 464 | 58 | 1,877 | 18 | 0.246 | 0.03 | 2.0 | 3 |
f0 and b0, unliganded opening and closing rate constants (s−1); E0, unliganded gating equilibrium constant (=f0/b0). Background: αA96H + εS450W (net fold increase in E0 = 1.7 × 105); n, number of patches.
Effect of background mutations, 11-Gly loop-C construct
| Constructs | f0 | ±SE | b0 | ±SE | E0 | ±SE | Fold change E0 | Fold change Echo2 | n |
| αA96H | 241 | 16 | 19,360 | 1,869 | 0.013 | 0.01 | — | — | 4 |
| +εS450W | 438 | 24 | 2,536 | 151 | 0.173 | 0.01 | 13.3 | 9.9 | 3 |
| +βT456F | 478 | 4 | 5,341 | 298 | 0.090 | 0.01 | 6.9 | 5.2 | 2 |
| +εL269F | 2,818 | 1,308 | 2.154 | 165.7 | 179.0 | 1 |
| Constructs | f0 | ±SE | b0 | ±SE | E0 | ±SE | Fold change E0 | Fold change Echo2 | n |
| αA96H | 241 | 16 | 19,360 | 1,869 | 0.013 | 0.01 | — | — | 4 |
| +εS450W | 438 | 24 | 2,536 | 151 | 0.173 | 0.01 | 13.3 | 9.9 | 3 |
| +βT456F | 478 | 4 | 5,341 | 298 | 0.090 | 0.01 | 6.9 | 5.2 | 2 |
| +εL269F | 2,818 | 1,308 | 2.154 | 165.7 | 179.0 | 1 |
11-Gly, a loop-C construct with 11 glycine residues substituted at positions α188–α198 in both α subunits (WT mouse sequence VFYSCCPTTPY; see Fig. 3). The mutation αA96H was present in all constructs to increase constitutive activity. +, the additional background mutation. Fold changes are relative to the no-additional-background construct, either without agonists (E0, 11-Gly construct) or in 20 mM choline (Echo2; WT-binding sites). n, number of patches. The effect of the added background mutation is similar with 11-Gly or WT C loops. Fold change Echoline2 values are from Mitra et al. (2004; εS450W and βT456F) and Jha et al. (2009; εL269F).
We also tested whether or not the 11-glycine construct could be activated by ACh. Fig. 3 B shows that there was no increase in the open probability when these AChRs were exposed to 1 mM ACh. We then examined another loop-C construct that had nine glycines and two tyrosines at positions 190 and 198 (9G/2Y). This construct, which had all four core aromatics at both binding sites, showed both brief and long unliganded openings. The brief open component had similar shut- and open-interval durations as the all-glycine construct (compare Fig. 3 A, 11gly, with Fig. 3 B, 0 ACh). With the 9G/2Y version of loop C, the application of >10 µM ACh did increase the cluster open-channel probability (Fig. 3 B). This indicates that with only two WT loop-C amino acids, neurotransmitter molecules could enter the binding sites with a low affinity, and that these sites could convert to a high affinity form to increase the open-channel probability.
Another relevant experimental observation supporting the priming mechanism was that the formation of a disulfide cross-link between cysteines at the tips of the C loops and the complementary subunits produced only what appears to be long unliganded openings. The interpretation given for this result was that forcing both C loops into their capped position leads to “double priming.” The effect of cross-linking only one C loop was not reported but according to this hypothesis should produce only “singly primed” brief openings. Interestingly, applying the same cross-linking protocol to AChRs that lacked the background gate mutations did not generate long unliganded openings. The reason given for this unexpected result was that without the distant gate mutations, loop C and the primary and complementary sides of the binding sites are too widely separated to allow a covalent reaction (Mukhtasimova et al., 2009; Sine, 2012), but experimental support for this speculation was not provided.
The cross-linking experiment demonstrates that making both C loops bond covalently with their complementary subunits increases the unliganded gating equilibrium constant. However, this rearrangement is substantial and likely to perturb many structural elements at the binding sites. This raised the possibility that cross-linking might be like other point gain-of-function perturbations that increase the gating equilibrium constant substantially simply by increasing the relative stability of O compared with the WT side chain (Jadey et al., 2011).
To test this, we measured unliganded gating in AChRs having several binding site point mutations. The mutations were not in loop C but in loop B (αG153S and αW149F), added to the βδ9′S background. The αW149F mutation by itself eliminates long openings, so all that remained were the brief gating events. Fig. 3 C shows unliganded gating activity from this construct in which both C loops were WT. The spontaneous activity of this construct resembled that from cross-linked AChRs with regard to cluster open probability.
Pathway
Another element of the priming model is that the ability to prime (transfer energy through the protein) depends on discrete secondary structures and residues in a specific site–gate linkage pathway. Our interpretation of the data presented in support of the priming scheme is that the capping of each C loop transfers energy to the ECD–TMD interface by a rigid body motion of β strands 9–10 (Lee and Sine, 2005; Mukhtasimova et al., 2009), and that the consequent perturbation of a proline (αP272, in the M2–M3 linker) and a salt bridge (between αR209 in the Pre-M1 linker and αE45 in loop 2) at this interface somehow (perhaps by a movement of loop 2) causes the displacement of the αM2 helix to trigger the channel conductance change. One piece of evidence presented for this set of rearrangements was that a mutation to a putative “on-pathway” residue, αP272A (at the ECD–TMD interface, in both α subunits), when added to the βδ9′S background, elicited only long unliganded openings, whereas one to a binding site residue not on this pathway (εP121L, on the complementary subunit, at the α–ε-binding site) elicited both brief and long unliganded events (see Fig. 1 A). The interpretation was that only the on-pathway mutation influenced (promoted, in this case) “doubly primed” gating.
We considered whether or not the observations could also be explained by local effects of the mutations rather than to the perturbation of a specific long-distance site–gate link. For instance, perhaps the αP272A substitution, but not the εP121L substitution, increases Po simply because the substituted side chain is more stable in O compared with the WT side chain. Like the loop-B mutations (Fig. 3 C) and cross-linking, the αP272A mutation might increase the gating equilibrium constant only by changing the relative ground-state energies rather than by perturbing an energy-transfer pathway.
To test this idea, we examined the effects on unliganded gating of several mutations that are likely to be either on or off the purported direct communication pathway, using the βδ9′S background (Fig. 4 A). Fig. 4 B shows that all of these mutations, some of which were not on the putative priming pathway, gave rise to AChRs showing only what appeared to be long openings. There was nothing particularly special about the location of the mutations, as substitutions in αM1, αM3, and αM4 all increased the unliganded open probability (Table 3). A straightforward interpretation of these results is that all of the mutations, including αP272A, make the system more stable in O compared with C and, hence, make the brief unliganded currents resemble the long ones that are apparent without the mutations.
Both on- and off-pathway mutations increase unliganded gating. (A) α-subunit interface and TMD of the Torpedo AChR (Protein Data Bank accession no. 2bg9; Unwin, 2005). The putative priming pathway is dark gray (see Fig 1 A). The mutated residues were in αM1, αM2, αM3, and αM4. (B) Example unliganded currents and open-interval histograms (the background was βδ9′S; arrow marks the time constant of brief component; see Fig. 2 A). All of the mutations made the brief openings longer-lived. The gating equilibrium constants are given in Table 3.
Both on- and off-pathway mutations increase unliganded gating. (A) α-subunit interface and TMD of the Torpedo AChR (Protein Data Bank accession no. 2bg9; Unwin, 2005). The putative priming pathway is dark gray (see Fig 1 A). The mutated residues were in αM1, αM2, αM3, and αM4. (B) Example unliganded currents and open-interval histograms (the background was βδ9′S; arrow marks the time constant of brief component; see Fig. 2 A). All of the mutations made the brief openings longer-lived. The gating equilibrium constants are given in Table 3.
Effects of mutations on unliganded gating
| Construct | f0 | ±SE | b0 | ±SE | E0 | ±SE | Fold change E0 | Fold change Echoline2 | n |
| βδ9′S | 351 | 34 | 5,021 | 534 | 0.074 | 0.01 | – | – | 9 |
| +αN217K | 1,262 | 62 | 223 | 24 | 5.9 | 0.90 | 81 | 43 | 4 |
| +αL279W | 1,855 | 102 | 147 | 21 | 13.4 | 2.66 | 182 | 156 | 3 |
| +αC418W | 2,402 | 205 | 286 | 43 | 8.7 | 0.76 | 117 | 110 | 4 |
| +α(N217T,C418Y) | 1,942 | 128 | 79 | 8 | 24.9 | 1.15 | 338 | 440 | 3 |
| +αS269I | 1,708 | 94 | 266 | 6 | 6.4 | 0.22 | 87 | 115 | 2 |
| +αP272A | 1,656 | 336 | 209 | 28 | 7.9 | 0.83 | 107 | 237 | 3 |
| DYS | 187 | 48 | 3,994 | 11,106 | 0.047 | 0.008 | – | – | 8 |
| εP121La | 229 | 17 | 5,068 | 285 | 0.046 | 0.01 | 1 | – | 5 |
| DYS+βL269D | 532 | 39 | 2,739 | 232 | 0.19 | 0.003 | – | – | 3 |
| εP121Rb | 23 | 4 | 5,633 | 255 | 0.0042 | 0.001 | 0.02 | – | 3 |
| Construct | f0 | ±SE | b0 | ±SE | E0 | ±SE | Fold change E0 | Fold change Echoline2 | n |
| βδ9′S | 351 | 34 | 5,021 | 534 | 0.074 | 0.01 | – | – | 9 |
| +αN217K | 1,262 | 62 | 223 | 24 | 5.9 | 0.90 | 81 | 43 | 4 |
| +αL279W | 1,855 | 102 | 147 | 21 | 13.4 | 2.66 | 182 | 156 | 3 |
| +αC418W | 2,402 | 205 | 286 | 43 | 8.7 | 0.76 | 117 | 110 | 4 |
| +α(N217T,C418Y) | 1,942 | 128 | 79 | 8 | 24.9 | 1.15 | 338 | 440 | 3 |
| +αS269I | 1,708 | 94 | 266 | 6 | 6.4 | 0.22 | 87 | 115 | 2 |
| +αP272A | 1,656 | 336 | 209 | 28 | 7.9 | 0.83 | 107 | 237 | 3 |
| DYS | 187 | 48 | 3,994 | 11,106 | 0.047 | 0.008 | – | – | 8 |
| εP121La | 229 | 17 | 5,068 | 285 | 0.046 | 0.01 | 1 | – | 5 |
| DYS+βL269D | 532 | 39 | 2,739 | 232 | 0.19 | 0.003 | – | – | 3 |
| εP121Rb | 23 | 4 | 5,633 | 255 | 0.0042 | 0.001 | 0.02 | – | 3 |
Backgrounds: βδ9′S, βL262S + δL265S; fold change E0 is relative to the background, and fold change Echoline2 is relative to the WT. The additional mutations have similar effects on the unliganded versus diliganded gating equilibrium constant. Fold change Echoline2 values are from Cadugan and Auerbach (2007; αL279W), Mitra et al. (2004; αC418W/Y [αC418Y alone increases Echoline2 by 71.3-fold]), Mitra et al. (2005; αS269I), and Jha et al. (2007; αP272A). Values for αN217K and αN217T were calculated from new measurements: fcholine2 = 2,543 ± 132; n > 3 patches; bcholine2 = 1,331 ± 109; E2: 1.96; and fcholine2 = 375 ± 44; bcholine2 = 1,319 ± 162; Echoline2: 0.29. For α (N217T + C418Y) the fold change in Echoline2 was the product for the value of the individual mutants (6.15 × 71.3 = 440).
DYS, α(D97A + Y127F + S269I) (Purohit and Auerbach, 2009).
DYS + βL269D.
Kinetic models
Additional support for priming was from kinetic modeling of single-channel currents in which the log likelihood was significantly greater for the scheme with “primed” states than for the Del Castillo–Katz scheme. In one experiment, AChRs with the βδ9′S background gave rise to alternating periods of activity having either brief or long openings, both without agonists as well as with low (1–10-nM) concentrations of ACh. Remarkably, the same kinetic scheme could be used to model both conditions, with rate constants for entering and leaving both the brief and long open states that were similar with and without ACh, but with long openings being more prevalent with ACh present. The interpretation was that at low agonist concentrations, “singly primed” gating episodes (with brief openings) still occur but that agonists increase the probability of “doubly primed” episodes (with long openings).
Many different kinetic schemes can describe single-channel currents equally well, so the assignment of a state in a single model to a physical state of the protein is not unambiguous. Our interpretation of the episodes with brief versus long openings at low [ACh] was different. A cyclic model for binding and gating has been used to describe AChR single-channel activity (Auerbach, 2010). Using this concept, we interpreted the brief opening periods as arising from completely unliganded AChRs (C↔O) and the long opening periods as arising from liganded gating activity (at low [ACh], mostly AC↔AO). In either case, in our model the arrow in each of these steps represents the same set of global allosteric transitions of the protein rather than “singly” versus “doubly” primed gating.
We tested the possibility that a cyclic mechanism might be able to account for the kinetic behavior of AChRs activated by low [ACh]. To make the modeling as simple as possible, we measured current interval durations at low [ACh] using a construct that had only one operational binding site. The construct had the mutations αW149F (to eliminate the unliganded long component), βδ9′S (to increase constitutive activity), and εP121R (to eliminate activation by the α–ε site). The αW149F mutation has two additional effects. First, it lowers the resting affinity, so it was necessary to use higher [ACh] than in AChRs without this substitution. Second, it reduces the energy generated by the affinity change for ACh. Previous studies using high [ACh] in otherwise WT AChRs showed that with αW149F, each ACh molecule increases the gating equilibrium constant only by ∼690-fold, compared with ∼6,000-fold in the WT (Purohit et al., 2012).
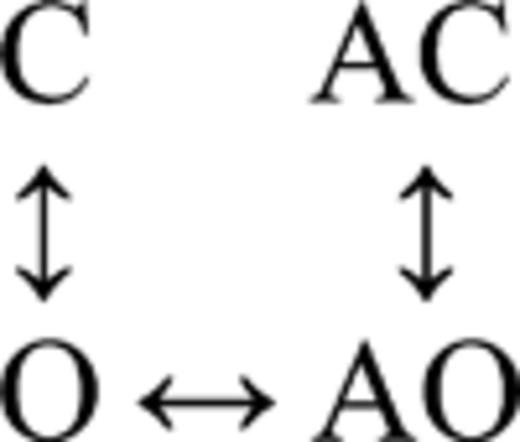
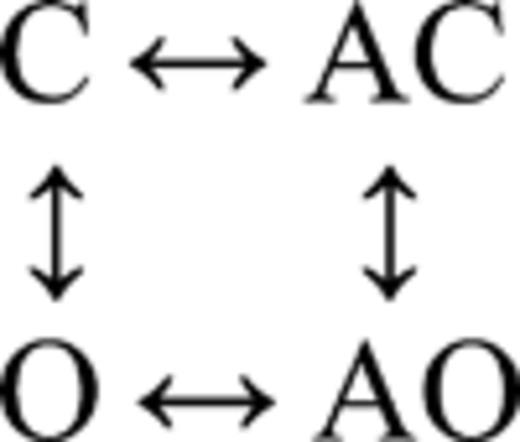
Fig. 5 A shows single-channel currents from the mutant construct at low [ACh]. Both brief and long openings were apparent, with relative proportion of the longer ones increasing with increasing [ACh]. We fitted the interval durations across concentrations using three different kinetic schemes, each having four states. In the first scheme, agonist binding connected only the C states (O↔C↔AC↔AO), and in the second scheme, agonist binding connected only the O states (C↔O↔AO↔AC). The third scheme was the full cycle in which agonist binding connected both the C and O states (Fig. 5 B, inset).
High affinity open-state binding estimated directly by using a cyclic kinetic model. The AChRs had the mutations αW149F (to eliminate long unliganded openings), βδ9′S (to increase constitutive activity), and εP121R (to eliminate activation by the α–ε-binding site). (A) Example single-channel currents. (Top) Low time–resolution view of clusters at 1 µM ACh (open, down). (Bottom) Higher time–resolution views at different [ACh]. Periods having only brief openings reflect unliganded C↔O gating, and those with long openings reflect mono-liganded AC↔AO gating. With increasing [ACh], the fraction of long opening periods increases. (B) Open-interval duration histograms at different [ACh]. Solid line is global fit across all [ACh] using a cyclic model (inset). Kd and Jd are the low and high affinity equilibrium dissociation constants; E0 and E1 are the unliganded and mono-liganded gating equilibrium constants. The fitted model parameters are given in Table 4. All of the rate constants, including ACh association to and dissociation from the high affinity open-channel conformation, can be measured in single-channel recordings.
High affinity open-state binding estimated directly by using a cyclic kinetic model. The AChRs had the mutations αW149F (to eliminate long unliganded openings), βδ9′S (to increase constitutive activity), and εP121R (to eliminate activation by the α–ε-binding site). (A) Example single-channel currents. (Top) Low time–resolution view of clusters at 1 µM ACh (open, down). (Bottom) Higher time–resolution views at different [ACh]. Periods having only brief openings reflect unliganded C↔O gating, and those with long openings reflect mono-liganded AC↔AO gating. With increasing [ACh], the fraction of long opening periods increases. (B) Open-interval duration histograms at different [ACh]. Solid line is global fit across all [ACh] using a cyclic model (inset). Kd and Jd are the low and high affinity equilibrium dissociation constants; E0 and E1 are the unliganded and mono-liganded gating equilibrium constants. The fitted model parameters are given in Table 4. All of the rate constants, including ACh association to and dissociation from the high affinity open-channel conformation, can be measured in single-channel recordings.
The goodness of fit for each model was assessed by its loglikelihood value (Qin et al., 1997). The best fit was obtained by using the full cycle (Table 4). Fig. 5 B shows that the open durations were well described by the optimal rate constants estimated from all [ACh]. The equilibrium constants for ACh binding to the low and high affinity conformation of the single operational binding site (α–δ with αW149F) calculated from these rate constants were 520 and 0.7 µM. The ratio of these constants gives the extent to which the gating equilibrium constant increases with an ACh molecule. The value obtained from the modeling studies (∼740-fold) is similar to that obtained previously by saturating the binding site (∼690-fold).
Fitting linear versus cyclic models to single-channel currents from AChRs activated by low [ACh]
| Model | kon | koff | f0 | b0 | jon | joff | f1 | b1 | LL | nfp |
 | 398 ± 39 | 5,457 ± 513 | 297 ± 3 | 8,883 ± 64 | – | – | 299 ± 7 | 234 ± 3 | 365,875 | 6 |
 | – | – | 303 ± 2 | 8,435 ± 63 | 470 ± 8 | 371 ± 6 | 2,911 ± 350 | 29 ± 2 | 366,151 | 6 |
 | 10 ± 1 | 5,086 ± 790 | 290 ± 12 | 8,404 ± 348 | 395 ± 19 | 272 ± 12 | 2,032 ± 182 | 78 ± 4 | 366,306 | 7 |
| Model | kon | koff | f0 | b0 | jon | joff | f1 | b1 | LL | nfp |
 | 398 ± 39 | 5,457 ± 513 | 297 ± 3 | 8,883 ± 64 | – | – | 299 ± 7 | 234 ± 3 | 365,875 | 6 |
 | – | – | 303 ± 2 | 8,435 ± 63 | 470 ± 8 | 371 ± 6 | 2,911 ± 350 | 29 ± 2 | 366,151 | 6 |
 | 10 ± 1 | 5,086 ± 790 | 290 ± 12 | 8,404 ± 348 | 395 ± 19 | 272 ± 12 | 2,032 ± 182 | 78 ± 4 | 366,306 | 7 |
In the full cycle (Fig. 5 B, inset), the agonist (A) could bind to both the C (low affinity) and O (high affinity) conformations. Rate constants (mean ± SD) were from the global cross-concentration fit (n = 64,790 intervals; s−1 or µM−1s−1). kon, low affinity association rate constant; koff, low affinity dissociation rate constant; jon, high affinity association rate constant; joff, high affinity dissociation rate constant; LL, loglikelihood; nfp, number of free parameters. fn and bn are the opening and closing rate constants with n-bound agonists. From the gating rate constants of the cyclic model, E1 = 26 and E0 = 0.035 (E1/E0 = 742).
These modeling results show that a simple cyclic reaction mechanism describes gating at low [ACh]. Further, they demonstrate that it is possible to measure directly both the agonist association and dissociation rate constants from the high affinity O conformation of the AChR. This is a new development in single-channel analysis.
DISCUSSION
The priming model for gating is intuitive from the perspective of AChR structure. It is reasonable to imagine that in channel opening, the agonist molecule at each binding site independently pulls in a C loop to tug strands β9–10, jostle a proline and salt bridge at an α-subunit ECD–TMD interface, tilt an αM2, and (with eventual help from the other α subunit) rearrange the gate region of the pore. It is also reasonable to associate one or more of these hypothetical intermediate structures with intermediate gating states that have been detected in single-channel recordings.
However, several experimental results do not support this clockwork sequence of domain motions. (a) The deletion of loop C does not inhibit unliganded gating (Fig. 3 A), so capping cannot be a requirement for pore opening. (b) Brief unliganded openings have the same conductance, voltage dependence, phi values, and O versus C energy difference as do diliganded openings and therefore do not reflect AChRs having only one activated α subunit. (c) The kinetics of single channels activated by low [ACh] are well described by a model having a single global gating conformational change rather than two independent subunit activations. (d) To a first approximation, agonists, mutations, voltage, and cross-linking change Po simply by changing the relative stability of O versus C, mainly by local interactions (Figs. 3 C and 4; Jadey et al., 2011). A perturbation-induced change in Po does not imply that the perturbed site is on a site–gate linkage pathway. (e) Mutant cycle analyses show that some closely apposed residues at the ECD–TMD interface are energetically coupled in gating (Lee and Sine, 2005; Purohit and Auerbach, 2007; Lee et al., 2008, 2009; Mukhtasimova et al., 2009; Mukhtasimova and Sine, 2013). This shows only that these side chains share a common environment and does not demonstrate that they participate in site–gate energy transfer. Energy coupling between neighboring residues is not evidence for allosteric energy transfer. (f) Nonconservative mutations of key residues at the ECD–TMD interface (for example, αP272S, αR209H, and αE45L) have almost no effect on Po, so it is unlikely that these amino acids are essential on–off switches that separate the C and O ensembles (Tamamizu et al., 1995; Lee and Sine, 2005; Lummis et al., 2005; Jha et al., 2007; Purohit and Auerbach, 2007; Paulsen et al., 2009; Mukhtasimova and Sine, 2013). (g) In channel opening, some residues at the C terminus of αM2 have higher phi values than those at the ECD–TMD interface: >0.9 (Bafna et al., 2008) versus ∼0.7 (Jha et al., 2007; Purohit and Auerbach, 2007). Insofar as phi gives the relative position of the energy change of a perturbed site within the allosteric transition on a scale from 1 to 0 (earlier to later) (Grosman et al., 2000), this result suggests the reverse order of energy change than as proposed in priming. These observations lead us to conclude that the mechanism of site–gate energy transfer in AChR gating remains an open question (Auerbach, 2013).
The kinetics of unliganded and mono-liganded gating at low [ACh] are consistent with a cyclic activation model that posits that unliganded and liganded gating are by the same essential mechanism (Fig. 5). The global Monod–Wyman–Changeux scheme for allosteric proteins remains a good, if approximate, model for AChRs (Monod et al., 1965; Karlin, 1967). For many years the sequential Del Castillo–Katz model (the physiologically relevant subset of Monod–Wyman–Changeux) has been the main scheme for estimating the low affinity binding and diliganded gating rate and equilibrium constants of AChRs. Protein engineering techniques have been developed to facilitate the measurement of the activation constants for mono-liganded and unliganded AChRs (Purohit and Auerbach, 2009; Jha and Auerbach, 2010; Nayak et al., 2012), and an indirect approach has allowed the estimation of the dissociation of ACh from the high affinity binding site (Grosman and Auerbach, 2001). The results in Fig. 5 show that it is possible to estimate directly the rate constants for unliganded and mono-liganded gating, and low and high affinity agonist binding, by using a single cyclic-state model. The ability to estimate the association rate constant between open states of the cyclic scheme is a new and significant development.
An observation that cannot be incorporated into the cycle is unliganded long openings. In some ways these resemble the long openings that are elicited by agonists. They are interrupted by brief gaps, and their lifetimes increase with background mutations that increase those of liganded events, suggesting that both classes of event are generated by the same essential C↔O gating process. However, in other respects the unliganded long openings are unlike those from agonists. A mutation of any one of the four core aromatic residues essentially abolishes them but does not affect or only modifies agonist-activated openings. For example, the binding site mutation αY198F has almost no effect on ACh affinity or efficacy (or desensitization) but eliminates completely the long unliganded events (Purohit and Auerbach, 2010).
We are unable at this time to propose a specific physical basis for long unliganded openings. They do not arise from activation by monovalent cations in the extracellular solution because they persist even when these are removed completely (Nayak et al., 2012). It is possible that that long openings are generated by water in the binding site (for example, OH+3) or by a structural fluctuation of the protein in the vicinity of the binding site (Purohit and Auerbach, 2010). Further experiments are needed to reveal the mechanisms that generate long unliganded openings.
Acknowledgments
We thank Marlene Shero, Mary Merritt, Mary Teeling, and Dr. Shaweta Gupta for the technical assistance.
This work was supported by National Institutes of Health (grants NS-23513 and NS-064969). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Author contributions: P. Purohit and A. Auerbach conceived and designed the experiments. P. Purohit performed the experiments. P. Purohit and A. Auerbach analyzed the data, and A. Auerbach wrote the manuscript.






![Figure 5. High affinity open-state binding estimated directly by using a cyclic kinetic model. The AChRs had the mutations αW149F (to eliminate long unliganded openings), βδ9′S (to increase constitutive activity), and εP121R (to eliminate activation by the α–ε-binding site). (A) Example single-channel currents. (Top) Low time–resolution view of clusters at 1 µM ACh (open, down). (Bottom) Higher time–resolution views at different [ACh]. Periods having only brief openings reflect unliganded C↔O gating, and those with long openings reflect mono-liganded AC↔AO gating. With increasing [ACh], the fraction of long opening periods increases. (B) Open-interval duration histograms at different [ACh]. Solid line is global fit across all [ACh] using a cyclic model (inset). Kd and Jd are the low and high affinity equilibrium dissociation constants; E0 and E1 are the unliganded and mono-liganded gating equilibrium constants. The fitted model parameters are given in Table 4. All of the rate constants, including ACh association to and dissociation from the high affinity open-channel conformation, can be measured in single-channel recordings.](https://cdn.rupress.org/rup/content_public/journal/jgp/141/4/10.1085_jgp.201210946/4/m_jgp_201210946_fig5.jpeg?Expires=1773786856&Signature=uRLzChizJjCGyICHXjXY5IVyrkpmevy7ZAWnZu6fJ80gE0GSW7M7RXjtO~Hd5pisKZ~fAAnSPZQOSpe5jqm8H9y7nILjDqnYD4AcvtJol432-lkCvgQOA-7v9petQksT~uDBcdpOGuZIHM1PlXZMrwzglVgs4orZXYIkwZs3wwwF8jBVdL7pnG-8TKxgvqf3U-It3UdATqShzkvoAcIZi5YGGLfqWu7rwLskf95UVoD32WWw8-hshGnVz8EqIKcpLTVaMrrIAqzh87fSRzlhKWNQJKnL7TLaxpSs-7bTawj5LoHfDZEJPRRvBTk4a2X6l2sNTDuk3nmwdkMZBjHyUA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)


