Inducible fluorescent speckle microscopy

Analysis of cytoskeleton dynamics by light microscopy benefits from the capacity to generate fluorescent marks along the otherwise uniform polymers. Fluorescence heterogeneity allows, for example, to distinguish a sliding microtubule from another that apparently slides owing to opposite polymerization dynamics at the tips, a process known as treadmilling (Margolis and Wilson, 1978). Such discrimination is crucial to identify force production mechanisms involved in biological processes such as cell migration and chromosome motion during cell division (Mitchison, 1989; Theriot and Mitchison, 1991; Waterman-Storer et al., 1998; Hu et al., 2007). In addition to filament translocation, turnover dynamics are undetectable using conventional fluorescence imaging but can be estimated from the lifetime of imprinted fiducial marks (Saxton et al., 1984).

Marking of cytoskeleton components is routinely done by incoherent imaging of a mask onto the sample to trigger a heterogeneous photoswitch (Axelrod et al., 1976), such as a photobleaching or a photoconversion pattern. This approach (which we term region-of-interest [ROI] switch) generates a pattern confined to a layer with a thickness defined by the objective’s depth of focus, which is of the order of λ/N.A.², where λ is the wavelength and N.A. is the numerical aperture. Whether the mask is generated in space (e.g., by a digital micromirror device) or in time (e.g., by gated scanning in a confocal head), mask structure is constrained to the instantaneous focal plane. Moreover, out-of-focus planes still experience a deleterious, homogeneous photoswitch. Thus, sequential z-stack imprinting cannot be used as a means to construct a 3D pattern.

Patterning in 3D can, however, be achieved by using fluorescent speckle microscopy (FSM; Waterman-Storer et al., 1998), where speckles are randomly created and tracked to infer the structure’s dynamics. FSM has been instrumental in uncovering key mechanisms involved in cell migration (Waterman-Storer et al., 1998), cell division (Maddox et al., 2002; Yang et al., 2008), and neuron growth cone dynamics (Medeiros et al., 2006), to give a few examples.

Because of the subdiffraction length of cytoskeleton’s polymer subunits, FSM often displays low contrast. As an example, when an isolated microtubule is being observed with a high-NA objective, the point-spread function (PSF) contains N ≅ 400 tubulin dimers, or severalfold this figure for a microtubule bundle, such as a kinetochore–microtubule fiber. As a result, and given that contrast scales as $1/N$ (Danuser and Waterman-Storer, 2006), speckle detection is seriously compromised.

Contrast in FSM can still be rescued by minimizing fluorescence background, which is indeed the defining feature of the FSM protocol. To achieve an adequate stoichiometry, FSM requires carefully controlled injection of small amounts of the fluorescent tag into cells (Waterman-Storer et al., 1998; Mendoza et al., 2012) or downregulation of gene expression, for example by using the leaky expression of an inducible GFP fusion tag (Goshima et al., 2005; Matos et al., 2009). The crucial aspect is that the required dilution of the fluorescent tag minimizes not only the background but also the useful signal to be detected.

To try to resolve this antagonistic signal–contrast coupling in FSM, we explore the possibility of forcing fluorescent molecules to clump together, stimulating formation of large clusters, or “metaspeckles.” As a result, and in the ideal case of PSF-sized clusters, the effective population inside a PSF would fall from 400 down to unity (N ≅ “1 cluster”), thus maximizing the $1/N$ factor that drives contrast level. Most importantly, high contrast would then be achieved without compromising signal, because each cluster is composed of a large number of fluorescent molecules, whose fluorescence intensities add together.

Implementation of this concept requires that positional correlations are imposed between fluorescent tags, so that clusters are indeed formed. Instead of resorting to putative intrinsic methods working at the sample level, we generate a 3D extrinsic (optical) speckle pattern comprising fine details down to the PSF scale, to be imprinted onto the sample by conventional photoswitching mechanisms.

As a proof of concept of this inducible speckle imaging (ISI) technique, we imprint speckles to measure microtubule dynamics within the metaphase mitotic spindle to test a postulated correlation between metaphase duration and the chromosome-to-pole microtubule transit time (Matos et al., 2009; Pereira and Maiato, 2012), here verified at the intraspecies level.

ISI requires that a granular beam is created with high-intensity 3D spots down to the PSF scale of the imaging system. This type of speckled beam can be generated by a narrow-band, polarized, spatially coherent light beam (Goodman, 1985), such as typical laser beams used in fluorescence microscopy, which is used to illuminate a diffuser (Figs. 1 a and S1). The bright and dark speckles thus generated are the manifestation of constructive and destructive interference of the waves scattered by the diffuser.

By using the microscope objective to direct the scattered light toward the sample, the ISI imprinting pattern is composed of speckles with dimension ≅λ/(2N.A.) (Dainty, 1984), which also turns out to be the approximate inherent imaging resolution for the same objective. Thus, speckle size always (approximately) coincides with the PSF of the objective, a convenient match that approaches the optimum condition, N ≅ 1 cluster (Fig. 1 b and Materials and methods). In addition, this convenient self-matching property releases the microscopist from recalibrating the speckle imprinting system for different objectives and wavelengths.

Using photobleaching or photoconversion, the sample of interest is exposed to the speckled beam until a significant fraction (e.g., 50%) of the fluorophores undergoes a photoswitch. As a result, a negative replica of the beam’s 3D structure becomes imprinted in the sample (Fig. 1, c and d). After this preparation stage, the now-speckled sample can be imaged in time-lapse mode by conventional means, such as wide-field or confocal microscopy, to determine kinetic parameters.

Efficiency of speckle imprinting is dependent on how large the laser intensity, I_laser, is relative to the typical intensity required to bleach the sample, I_bleach. We thus define an adimensional control parameter, the ISI strength (γ), through the equation:

where $〈 〉$ stands for a mean across the (heterogeneous) imprinting beam. ISI strength is thus a global parameter used to control the extent of the perturbation, being defined in multiples of the bleaching level of the fluorescent tag.

To characterize ISI, it is required that the structure of the fluorescent pattern is known (statistically), which depends not only on the structure of the imprinting beam but also on the character of the transfer process, assumed here to obey a first-order reaction photoswitch (Axelrod et al., 1976; Bjarneson and Petersen, 1991). Defining f as the ratio between the post- and pre-ISI fluorescence at a given point, f = I_post/I_pre, we find it to be distributed throughout the sample according to a power law histogram $P F (f)=γ −1 f γ −1 −1$ (Materials and methods and Fig. S2 a). Two important quantities can be retrieved directly from P_F(f), namely, contrast C_ISI, and the mean remaining fluorescence $〈 f 〉$⁠, which are given by the following equations (Materials and methods):

and

In practice, γ in a given imprinting experiment is retrieved a posteriori through Eq. 2, which requires measuring the remaining fluorescence level in the perturbed ROI.

Consistent with the aim of maximizing both contrast and fluorescent signal, we define the contrast-signal product (Eq. 1 multiplied by Eq. 2) as the ISI quality parameter to be maximized, here termed “speckle amplitude” and denoted by σ_f. From the definition, speckle amplitude is thus the SD of the fluorescence fluctuations across the sample. For γ = 1, which will be seen to nearly maximize speckle amplitude, high contrast is generated after depleting 50% (see Eq. 2 and Fig. S2 b) of the fluorescence signal (by photobleaching), which compares to the 99% depletion (by dilution) typical of FSM (Danuser and Waterman-Storer, 2003, 2006).

Optical speckle patterns were generated using single transverse mode (TEM₀₀) laser beams at 488 or 405 nm to illuminate a holographic diffuser placed in one of the microscope’s filter turret slots (∼10 cm from a 1.4-NA 100× microscope objective back focal plane). To test performance in cells, speckles were imprinted on the mitotic spindle of cultured Drosophila melanogaster primary cells, as well as Drosophila S2 and human U2OS cells, using either photoconversion (mEos–α-tubulin, 405-nm laser, typical 500-ms pulse length) or photo-bleaching of a conventional fluorescent tag (GFP–α-tubulin, 488-nm laser, typically with a 500-ms pulse length; Videos 1 and 2 and Figs. 2 a and S3 a). After removing the diffuser from the optical path, spinning-disk confocal imaging is performed to image the sample (Fig. S1; see Materials and methods for optical setup details).

The fluorescence pattern after an imprinting pulse is 3D (Fig. 2 b and Videos 3, 4, and 5), being therefore unrelated to the particular focal plane at the time of the imprinting. The pattern is also insensitive to aberrations, weak scattering, and depolarization, creating deep speckles even in thick tissue (Fig. S3 b). These features, which are intrinsic properties of optical (ISI) speckles, contribute to a robustness and swiftness of operation unseen in conventional ROI switch modes, including the possibility of refocusing after imprinting (Video 3).

The 3D pattern is more naturally and less invasively generated by FSM, which does not involve a perturbing optical pulse, but there the control parameter (tag concentration) requires finding cells with the appropriate expression level or alternatively meticulously injecting each given cell, only to achieve modest contrast-signal products. A comparison between populations of FSM and ISI cells illustrates that, in addition to a higher throughput, ISI generates higher-amplitude speckles (Fig. 2 c and Video 6) while not compromising phenotypic cell analysis by backtracking toward pre-ISI imaging, which is unperturbed (Video 7 and Table 1). Nonetheless, FSM displays higher-amplitude speckles at the edge of the diffraction limit, evidencing a relevant virtuous byproduct of the mismatch between FSM and the microscope’s bandwidth (Fig. S4, a and b).

For speckle imprinting to be useful, the structure of interest (in this case, tubulin) must be static at relevant timescales, namely, ISI pulse duration and imaging exposure. That is not the case for cytoplasmic tubulin, which rapidly reorganizes by diffusion, effectively allowing time for the declustering of molecules composing each speckle. As a result, a PSF volume imaged in the cytoplasm shortly after the pulse (≥ms) already contains a mixture of “bright” and “dark” molecules, which are unrelated to the initially imprinted speckle pattern. Therefore, as shown in Fig. 2 d, the first post-ISI acquisition already displays a cytoplasmic field with a nearly homogeneous fluorescence level of f = (1 + γ)⁻¹ (Eq. 2). This rapid fadeout naturally limits the ability to probe fast diffusive processes, for which nonimaging techniques are typically more adequate (e.g., fluorescence correlation spectroscopy), but it can be regarded as a useful background rejection method whenever the particular process under study can be temporally resolved by sequential imaging.

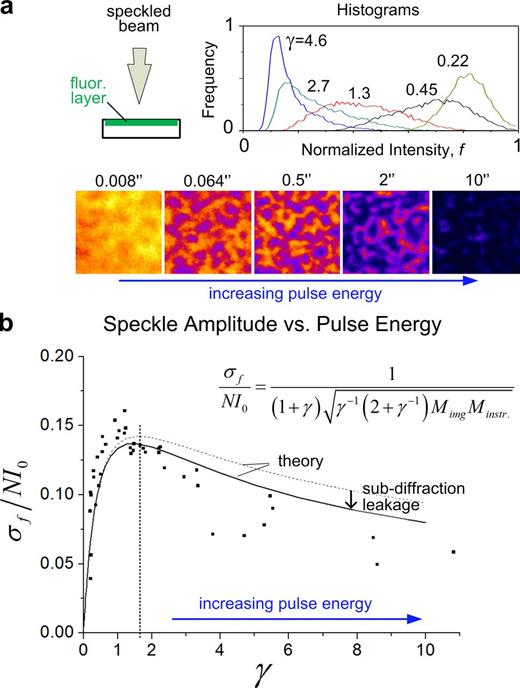
ISI performance was then tested as a function of γ by imprinting speckles on a thin, homogeneous, and static fluorescent layer (concanavalin A–Alexa Fluor 488 conjugate; Fig. 3 a). Speckle imprinting is observed to be poor at the lowest, as well as at the highest, γ levels. Indeed, a very weak pulse (γ ⪡ 1) barely has an impact on sample fluorescence, which remains uniform, whereas a strong pulse (γ ⪢ 1) saturates the photoswitch probability, ultimately driving the sample back to uniformity, but now because of the lack of fluorescent molecules. This indicates that an optimal pulse energy exists that promotes a more heterogeneous switching. We found from theoretical calculations that maximal speckle amplitude would occur when γ = Φ, with Φ (≈1.618) being the so-called golden ratio or golden section (see Materials and methods). It can be seen from Eq. 2 that this optimal imprinting strength leaves a 2 − Φ (∼40%) remaining fluorescence signal, which compares to the 1% in typical FSM conditions. Experimental data (Fig. 3 b) displays the expected speckle amplitude dependence on γ and identifies the optimal γ range, providing the microscopist a simple rule and readout (“40% after-pulse remaining signal”) to optimize speckle imprinting.

In addition to the sample pattern, modeling the actual experimental scenario requires accounting for imaging the sample. We calculated theoretically that the effect of the sample-to-detector path accounts for an 30% unavoidable contrast loss, which applies to virtually any optical setup in an “epi” configuration (Fig. S4 a; see Materials and methods). This baseline value slightly increases with γ because of the increasing formation of subdiffraction speckles (Fig. S4, b–d; and Materials and methods). The final model curve that relates speckle amplitude to laser pulse energy is (Fig. 3 b)

where the numerator stands for the fluorescence signal that would be emitted by a fully occupied lattice (comprising N fluorophores, each contributing a signal I₀), M_img is the theoretically calculated sample-to-detector factor (Fig. S4 d and Materials and methods), and M_instr. arises as the single fitting parameter of the model curve, to account for instrumental smoothing of the speckle pattern (e.g., because of imperfect laser polarization and finite pixel size). The optimal laser pulse energy and the scale of associated speckle amplitude are thus confirmed experimentally (Fig. 3 b).

Speckle displacement and speckle contrast fadeout can be used to assess sample dynamics. Displacement of a speckle reflects a coherent collective motion of its components (multiple fluorophores) and can therefore be trivially used to determine velocity over distances greater than the spatial resolution scale of the microscope. Speckle contrast fadeout, on the other hand, reflects incoherent motion of its components, or declustering, allowing determination of diffusion properties or turnover timescales. Specifically, declustering drives the system from the ISI regimen toward an FSM-like regimen, which is reached when positional memory is completely lost (Figs. 1 b and 4 a).

To prove the principle, microtubule turnover dynamics were measured in the context of the mitotic spindle, where microtubules within a kinetochore fiber are kept within a certain stability window (Matos et al., 2009; Bakhoum and Compton, 2012), the boundaries of which define a rising probability for aneuploidy-promoting events. In general, microtubule lifespan runs in the range of seconds to minutes, which may be detected as a temporal fadeout of an imprinted pattern, caused by the random supply of cytoplasmic tubulin dimers to the forming replacement microtubules (Fig. 4 a).

To measure spindle microtubule turnover in Drosophila S2 cells (Buster et al., 2007; Goshima et al., 2008), speckle patterns were imprinted using ∼200- to 500-ms-long pulses, with a mean strength of γ ≈ 1.7 (Fig. 4 b and Video 8) and microtubule lifetime calculated from the mean of contrast–time curves obtained in independent experiments (Fig. 4, c and d). As expected, treatment with a microtubule-stabilizing drug (Taxol) generates a plateau (40%) in the turnover curve, indicating the presence of a significant pool of microtubules that persist for a time much longer than the duration of the experiment (Video 9). Importantly, the directly measured curve in an ISI experiment (contrast decay) has a simple relation to sample turnover. As an example, the timescale at which an exponential contrast decay occurs is related to the structure’s effective lifetime through $τ eff =1 2 τ contrast$⁠, the factor of 2 being rooted in the twofold contribution of (a) bright speckles, which fade out to the mean value, and (b) dark speckles, which fade in to the same mean value (Materials and methods). The more general outcome, applicable to the single-exponential or any other model, is that the biologically relevant turnover curve (rate of loss of original microtubules) is retrieved from the square of the measured contrast curve, C² (Fig. 4 d and Materials and methods).

Imprinting of fiducial marks on metaphase spindle microtubules uncovers a persistent flow from the spindle equator toward spindle poles (Fig. 5 a and Video 10). This process, known as microtubule poleward flux (Mitchison, 1989), has been observed in the majority of animal and plant cells investigated to date. With the aim of exploring how flux scales with metaphase spindle architecture across cell types, we used ISI to measure flux in primary ex vivo samples of Drosophila melanogaster, namely, ganglion mother cells, neuroblasts, and ovarian follicle cells and also S2 cultured cells, all stably expressing GFP–α-tubulin under the control of a strong promoter (see Materials and methods). In these samples, FSM is essentially inapplicable because of the difficulty in controlling fluorescent tag concentration and the low signal–contrast speckles, which aggravates the impact of spherical aberration on deep imaging.

To compensate for the different optical conditions of these samples, the ISI beam pulse energy was tuned to approach γ ≅ 1.5 in each cell type. Flux velocity in each cell type was calculated by measuring the slope of fluorescent (or nonfluorescent) speckle tracks in guided kymographs (Fig. 5 a and see Materials and methods) generated from post-ISI time-lapse acquisition.

The obtained flux (F) data are shown against spindle length (2L) in Fig. 5 b for the different cell types, with each cell type occupying an identifiable domain (2 σ error ellipses in Fig. 5 b), although a correlation trend is not observed. As a more meaningful correlation, it has been hypothesized that the ratio L/F, which has dimensions of time, defining a spindle-scale mechanical equilibrium “clock,” could be correlated to the biochemical clock, τ_meta, that defines metaphase duration (Matos et al., 2009). Mathematically, the expected correlation is simply τ_meta ≈ L/F, the right-hand side being retrieved directly from the data in Fig. 5 b.

It is observed that the data points broadly satisfy the equality, thus populating an optimal cone (green cone in Fig. 5 c). These results strengthen the view that, within a mechanically coupled spindle (Matos et al., 2009; Charlebois et al., 2011), degradation rates of the anaphase-promoting complex substrates match the mechanical relaxation timescale, so that anaphase typically starts within a small time window just after a mechanical equilibrium is reached. Whether this clock matching is passive (e.g., throughadaptation) or active remains to be answered.

Measurement of the persistent poleward flux of microtubules during mitosis has been hampered by the lack of an amply applicable method for generating artificial fluorescent 3D structure in naturally homogeneous objects. The available techniques, FSM and ROI switch (e.g., FRAP and fluorescence dissipation after photoactivation), display sets of advantages that are essentially mutually exclusive (Table 1). There are a number of experimental scenarios in which the technique we describe has the potential to combine these sets of advantages, namely, (a) the aberration-insensitive and 3D character of FSM-created speckles and (b) the high signal–contrast, optically controlled marking, sample availability, and uncompromised preimaging that characterize ROI switch.

The conceptual advantage of ISI over FSM stands on the inhibition of subdiffraction speckle formation (Fig. 1 b). The end result is that ISI power is spent only in writing structures that can effectively be read, whereas FSM spends a large power fraction in creating speckles that are not discernible and that will contribute to background only (see typical power distribution in Fig. S4 b). As a corollary, FSM-based speckles display signal-contrast levels comparable to ISI only when a microscope with a resolution of the order of the dimension of the subunits involved is used (Materials and methods). Additionally, ISI can be used with the large collections of cell lines or transgenes constitutively expressing GFP (or other) fusion proteins that are readily available from existing repositories (“sample availability” parameter in Table 1). These characteristics, which in these respects bring the method closer to ROI switch, may contribute to a wider use of speckle imaging, including laboratories without access to microinjection or high-sensitivity detection systems.

Although the comparison between ISI and FSM seems generally favorable to the former, it is clear that ISI is optically more invasive by requiring an optical perturbation trigger, even though photodamage during imaging is potentially lower because of the stronger available signal (Table 1). Furthermore, ISI has a limited population of speckles near the diffraction limit, leaving a spectral window at the high-resolution edge where FSM indeed surpasses ISI. Thus, the dimension of imprinted speckles is comparable but larger than that found in FSM (Fig. S4 b). We also confirmed that, in typical experimental conditions, ISI speckle size is comparable to (but larger than) the PSF of the microscope (Fig. S5 a).

Although widely applicable, ISI and FSM are stochastic techniques, adequate only when the precise position of the marks is irrelevant, which is often the case when studying structures that are long and homogeneous along at least one dimension. Examples within this class are membranes, gels, and cytoskeleton filaments. In contrast, deterministic approaches (ROI switch) have, by definition, a broader range of applications, but implementation is more costly, complex, and only justifiable if pattern prescription is indeed required. Also, 3D marks cannot be created by conventional ROI switch, but only by using so-called holographic techniques, which add to complexity and cost. More fundamental, however, is the fact that ROI switch patterns are sensitive to aberrations of the optical system and to scattering in deep samples. In contrast, speckles created by random wave interference (ISI) are immune to aberrations, given that these will modulate or randomize an optical beam which was already random (because of the diffuser), therefore leaving essentially no trace in the generated speckle pattern (Dainty, 1984). Admittedly, this inherent robustness of the ISI technique solves only half of the problem, for the speckled object still has to be imaged by such aberrated imaging system.

In practice, we found ISI to be a very attractive technique for measuring microtubule poleward flux in a variety of systems that are not easily accessible by FSM. Turnover measurements, however, can be seen to display strong fluctuations before averaging (Fig. 4 d), which are caused by focus fluctuations, hot pixels, and the unavoidable morphological dynamics of the structure itself, among other factors. In general, however, these are as problematic in ISI as they are in ROI switch (FRAP or fluorescence dissipation after photoactivation). That is not the case for the effect of signal attenuation (e.g., instrumental photobleaching), however, which in ROI switch needs to be uncoupled from the sample-associated intensity curves. This problem is more naturally circumvented in ISI by making use of contrast, which is insensitive to attenuation (Materials and methods).

In future developments, we anticipate that ISI measurements, such as speckle translocation and fadeout, can strongly benefit from robust algorithmic approaches developed in the context of FSM or particle image velocimetry (Danuser and Waterman-Storer, 2006; Mendoza et al., 2012). Indeed, speckle tracking and deep analysis of contrast–time curve shapes can, in principle, yield refined information on complex kinetics processes (e.g., anomalous diffusion), especially if combined with a fast setup (e.g., dual-wavelength; see Materials and methods) capable of probing very short timescales.

Using a first-order approximation to describe the fluorophore transition to the bleached state after irradiation (Axelrod et al., 1976), the local fraction f of particles remaining fluorescent after the bleaching pulse is $f(r → )=exp( −I laser (r → ) /I bleach )$⁠, where I_laser is the local optical intensity and I_bleach is the characteristic bleaching intensity (a property of the fluorescent tag). Knowledge of the statistics governing f requires knowledge of the statistics governing I_laser (i.e., speckle statistics) which, in the single-mode case, follow a negative exponential also (Goodman, 1985). Using the usual method for transformation of random variables, it follows that the fluorescence intensity probability density function after the ISI pulse on a uniform sample is given by a power law:

where the adimensional parameter γ, the bleaching strength, is the single control parameter of the imprinting process, defined by $γ≡〈 I laser 〉 /I bleach$⁠.

It can thus be seen that the characteristic negative-exponential histogram of speckle patterns is efficiently decompressed by simple photoswitch mechanisms. This combination evokes a spreading of the sample fluorescence histogram, resulting in increased contrast (Fig. S2 a).

The nth moment of P_F(f) (Eq. 4) is given by (1 + nγ)⁻¹, from which the centered second moment (or variance) is found to reach a maximum when $γ=0.5( 1+5 )≅1.618$⁠, the so-called golden ratio, corresponding to a first moment (mean fluorescence signal) $〈 f 〉≅( 1+1.618 ) −1$⁠, or almost 40%.

We recast now the generality of the aforementioned results by saying that the golden ratio maximizes the amplitude of the fluctuations (in the standard-deviation sense) in the general physical setting where a negative-exponential response mechanism is probed by a negative-exponential process.

The value of the maximal speckle amplitude is found to be $σ f ISI =0.3NI 0$⁠, where N is the number of taggable sites inside a PSF (∼400 in a microtubule) and I₀ is the single-molecule fluorescence signal. This optimal pulse allows (1 + Φ)⁻¹ or, equivalently, a 2 − Φ fraction of the fluorophores to remain in the active state. The comparable situation in FSM, in which the same 40% signal remains available (relative to full occupancy), yields for the speckle amplitude a square-root dependency $σ f FSM ≅0.5N I 0$⁠, which compares to the linear scaling with N in ISI.

FSM space-dependent signal can be described by a binomial distribution with parameters N, the number of taggable sites inside the measurement domain (a PSF, in this case), and p, the occupancy probability of each site, which is independent of the occupancy status of the neighbors. The mean and variance of the number of fluorescent particles inside a PSF are then Np and Np(1 − p), yielding a contrast

which is written in the form $1/M$ to emphasize its equivalence to a contrast loss factor derived from the addition of M independent processes (Goodman, 1985). Contrast in ISI is given by Eq. 1 in the main text, which, using Eq. 2 and assuming an initially fully occupied lattice, can be rewritten as:

where N_ISI = 2 + p/(1 − p), which is to be compared with N_FSM = N in Eq. 5. This shows that, for example, when p = 0.5, ISI behaves as FSM would in the case of a PSF enclosing three subunits only. Such an FSM regimen would require deep superresolution techniques to be used in live imaging of cytoskeleton polymers.

To estimate contrast in the detected signal, one has to take into account diffraction losses upon light propagation toward the detector. This is best understood by considering the spatial frequencies involved. The power spectral density (PSD) of a single-mode speckle pattern in the far-field, S_speckle(k), is given by the autocorrelation of the pupil function (ISI curve in Fig. S4 b; Goodman, 1985). The optical transfer function (OTF) of a focused, aberration-free, imaging system is also given by the autocorrelation of the pupil function (Goodman, 2005). This equivalence, S_speckle(k) = OTF(k), is reminiscent of a formal equivalence in coherence theory expressed by the Van Cittert–Zernike theorem (Wolf, 2007). At low strength (γ ⪡ 1), the imprinted fluorescent pattern is an inverted replica of the laser speckle pattern, maintaining the PSD intact. Thus S_in(k) = OTF(k) (Fig. S4 b).

Using the fact that S_out(k) = |OTF(k)|² S_in(k) applies when imaging a random scene (O’Neill, 2004), it follows that the power spectral density of the incoherently imaged speckle pattern is given by S_out(k) = OTF³(k), where real valuedness of the (aberration-free, nondefocused) OTF is assumed. It can be seen that the number of equivalent-modes, M_img, implicated in imaging the fluorescent speckle pattern is then (Fig. S4 c)

Thus, for a circular pupil and γ ⪡ 1, M_img ≈ 2.12, accounting for an $1/2.12$ contrast preservation or 30% contrast loss relative to that measured at the sample. (For a rectangular pupil, the result is M_img = 2.) Note that these “2.12 modes” describe the degrees of freedom (or modes) in the general case of an optical speckle pattern that suffers decoherence and is imaged through the same circular pupil that generated it (Fig. S4 a).

The integrals quotient above is applicable to calculate the number of modes for any γ, provided a reasonable photoswitching model is available to allow estimation of subdiffraction spreading of the PSD at high saturation (Fig. S4 c). For the simplest estimate, we use a first-order reaction approximation for photobleaching (Axelrod et al., 1976) and calculate the power spectrum of the fluorescence pattern by speckle simulation in MATLAB (MathWorks). A seventh-degree polynomial was fitted to the values obtained for M_img (γ) (Fig. S4 d) and fed into the model curve before running the fitting routine (Fig. 3 b). We recall that the single fitting parameter, M_instr., is an instrumental factor accounting for speckle smoothing, such as that resulting from imperfect polarization of the imprinting beam and spatial undersampling (Goodman, 1985; e.g., finite pixel dimension). For formal convenience, an equivalent mode number may also be assigned to ISI, which is then recast as M_ISI = γ⁻¹(2 + γ⁻¹) (see Eq. 1). All mode numbers (M_img, M_instr., and M_ISI) are heuristically assumed to be independent, allowing their multiplication to determine an overall mode number and therefore a total contrast loss (M_ISI⋅M_img⋅M_instr.)^−1/2 relative to the incident laser beam’s contrast (which is typically close to 1).

Notably, it is found that smoothing of the imprinting laser pattern does not always lead to a smoothing of the imprinted fluorescence pattern (Fig. S5 c). This less intuitive regimen is most simply observed in a two-mode imprinting scheme under a high saturation regimen (γ₁ + γ₂ > 2), where indices 1 and 2 represent different imprinting modes, such as independent polarization components of the imprinting beam where the moments of the distribution are given by:

This situation, in which contrast can be increased by decreasing the spatial coherence of the imprinting beam, can be understood by recognizing that in such strong bleaching regimen bright laser speckles lead to a strong depletion of fluorescent molecules in those regions. In such case, and if contrast is to be further increased, it is more efficient to add the needed extra amount of energy through a second mode than through the original mode, so that neighboring, not-yet-depleted regions (which retain high susceptibility to bleaching) are affected by the ISI pulse.

Acousto-optic tunable filter (AOTF)–modulated 488- and 561-nm CW lasers (100 and 50 mW; Coherent Sapphire) were used for fluorescence excitation. The 488-nm laser and an additional 405-nm diode laser (Coherent OBIS; through direct modulation) were used for speckle imprinting in photobleaching and photoconversion modes, respectively. Both the AOTF RF-driver and the 405-nm laser modulation port are fed by a digital-to-analog converter (DAC PCI-6733, National Instruments) controlled by NIS-Elements software (Nikon).

When using the same laser for both bleaching and fluorescence excitation (at 488 nm), switching between the respective optical paths is done by slide in/out of a half-wave plate at the appropriate angle to rotate light polarization by 90°. This operation is performed after the AOTF and before a polarizing beam-splitter (PBS; Fig. S1). The two PBS outputs are followed by fiber-coupling lenses and polarization-maintaining single-mode fibers (Solamere Technology), one coupled to the spinning disc head (CSU-X1; Yokogawa) and the other steered toward the microscope at the level of a secondary filter turret in the inverted microscope (TE2000-U, with stage-up kit; Nikon), thus bypassing scanning, as required for single-mode speckle generation.

Apart from (self-)diffraction, the nearly collimated ISI laser beam (∼1/e² waist diameter of 0.8 mm at the single-mode fiber exit, or ∼1 mm after diffracting over ∼1-m propagation toward the diffuser) is not transformed by lenses or other refractive elements before hitting the diffuser. A holographic diffuser (CVI-Melles-Griot HD-0.5–25.0) occupies a slot in the upper filter turret to generate the speckle pattern in the sample after a plan-apochromatic 1.4-NA 100× DIC objective (VC series; Nikon). In principle, any diffuser can be used that imparts a spatially random phase shift with fluctuations in excess of 2π and that scatters light into a cone filling the back aperture of the objective, making full use of its N.A. The latter condition is essential to guarantee that the PSD of the speckle pattern intensity matches the OTF of the imaging system, meaning that structures down to the diffraction limit are indeed imprinted in the sample.

The linear dimension at the sample that is affected by the optical speckle pattern is given approximately by the ratio between the laser beam diameter at the diffuser and the objective magnification, provided the distance between the objective and the diffuser roughly equals the standard 200-mm tube lens focal distance. Decreasing this distance by a given factor (which in our setup is ∼2) increases proportionally the ROI linear dimension at the sample. An ∼20-µm-diameter ISI-effective ROI is obtained in our setup.

Optical power at the sample plane with full AOTF transmission is ≈8 mW, with RMS fluctuations <3%. The optical power density was sufficient to perform ISI (1 < γ < 2) with 100- to 500-ms typical exposure times, without the need for additional (collector) optics between the diffuser and the microscope objective. Post-ISI imaging optics include an achromat lens to image the spinning disc pinholes onto an EM-CCD (iXon897; Andor), the overall sampling being 112 or 75 nm/pixel when using a 1.5× optivar.

Operationally, switching from imaging to ISI mode involves rotation of the lower filter turret (to insert the wideband reflecting dichroic [FF605 Di-02; Semrock], thus enabling the ISI path at the microscope), rotation of the upper filter turret (to insert the diffuser) and insertion of the half-wave plate between the AOTF and the PBS to divert the beam from the spinning disc-injecting fiber to the ISI-injecting fiber. A faster (no-lag) setup may be useful to study fast processes and can be implemented by using a shifted-wavelength bleaching laser (e.g., 473 nm) and an appropriate dichroic reflecting at 473 nm but allowing excitation (transmission) at 488 nm.

Temperature in an incubator around the sample holder and objective revolver is kept constant by an Air-Therm ATX heater (World Precision Instruments) at 25°C, with the exception of U2OS cells (maintained at 37°C).

Neuroblasts and ganglion mother cells were obtained by brain dissection of Drosophila third-instar larvae brains and plated in Schneider culture medium supplemented with 10% FBS on #1.5 coverslips. Partial stabilization of the sample was achieved by covering the brain with a low-melting-temperature agarose-based layer (approximate thickness, 170 µm) which was also supplemented with 10% FBS after cooling down to room temperature. Evaporation/leakage of the medium was prevented by sealing the preparation with VALAP (1:1:1 vaseline/lanolin/paraffin; Pereira et al., 2009). Ganglion mother cells were distinguished from neuroblasts by the nearly twofold diameter difference. For live imaging of ovarian follicle cell division, intact Drosophila ovaries were dissected into Halocarbon oil 700 (Sigma-Aldrich) as previously described (Weil et al., 2012).

Thin fluorescent layers (experiments in Figs. 1 c and 3, a and b) were prepared by coating coverslips with Alexa Fluor 488–conjugated concanavalin A (Molecular Probes). For FSM, S2 cells stably expressing GFP–α-tubulin under the control of a leaky inducible metallothionein promoter were used. In the absence of the promoter, low (leaky) levels of GFP–α-tubulin are expressed, as required for FSM. U2OS mEos–α-tubulin cells (Wandke et al., 2012; a gift from S. Geley, Innsbruck Medical University, Innsbruck, Austria) were grown in DMEM with 10% FBS on glass-bottom dishes (Matek) at 37°C. Drosophila S2 cells were grown in Schneider medium with 10% FBS on concanavalin A–coated glass-bottom dishes (#1.5; Matek).

Flux velocity was measured through the slope of speckle tracks in guided-kymographs in a custom routine written in MATLAB. These guided kymographs were generated after manual spindle pole tracking, the coordinates of which are used to compensate for spindle rotation and translation during kymograph generation, thus stabilizing a virtual equator (as defined by the normal bisector of the pole-to-pole connecting line) in the horizontal center of the kymograph.

Metaphase duration was estimated by measuring the time that chromosomes maintain alignment at the metaphase plate (30-s resolution), which is assumed to reflect the degradation timescale of anaphase-promoting complex substrates. Spindle length and flux velocity were measured using a custom-written MATLAB code. For spindle length, measurements were performed manually using the microtubule “focal points,” not the (often detached) centrosomes, as references.

To calculate turnover, a rectangular ROI was defined enclosing a significant portion of the spindle area. Intensity contrast, defined as $C≡σ I /〈 I 〉$⁠, was then determined at each time point of the acquired sequence after the subtraction of a preacquired mean dark reference level from each frame. The microtubule turnover half-time was calculated by fitting a double-exponential curve (y₀ + a₁ exp[−(t − t₀)/τ₁] + a₂ exp[−(t − t₀)/τ₂]) to the square of the mean of independent experiments (i.e., cells) for each time point. Before averaging, contrast curves were normalized to a 0-to-1 contrast change defining the pre- and post-ISI transition.

The timescale calculated for contrast decay is twice the timescale of microtubule turnover for a single-exponential process. The factor of 2 may be understood by recalling that the variance of the sum of independent random processes is equal to the sum of their individual variances, or

where we assume equivalent experiments. Here, one “experiment” is a microtubule, which may still display ISI-induced intensity fluctuations (σ ≠ 0) or not (σ = 0), in case it was polymerized already after the ISI pulse. Calling the number of surviving microtubules at a given time point n(t), then $σ eff 2 =n( t )⋅σ 2$ or, for the contrast $C eff =n( t ) ⋅C$⁠, meaning that $n( t )∝C eff 2$⁠. This is the main result that links contrast dynamics to the biologically relevant dynamics. Assuming that n(t) follows an exponential decay, then C_eff = exp[−t/(2τ)]. For a double exponential, coupling occurs between timescales, making it a more robust approach to calculate C² before fitting. As in other methods, fluctuations of spindle position relative to the focal plane, or other structural changes within the spindle that modulate the spindle image contrast over time, cannot be easily compensated for, and therefore introduce noise into the measurements.

Time-lapse imaging may induce unintentional bleaching, which in a typical ROI switch quantification requires performing an experimental decoupling of biological and instrumental signal fading. With ISI, because many bright and dark speckles are simultaneously present, each population acts as a control for the other population, which becomes explicit by the fact that a normalized quantity (contrast) is being calculated, rather than an “absolute” intensity. Explicitly, the measured contrast is $C bX =bσ X /( b〈 X 〉 ) =C X$⁠, where X is the quantity being measured (intensity) and b is the attenuation factor (e.g., caused by bleaching during imaging), which effectively cancels out in the contrast calculation. Thus, two images that differ by a multiplicative factor have the same contrast.

Far-field speckle patterns in Figs. 1 and 4 were generated in MATLAB with the following steps (Duncan and Kirkpatrick, 2008). (a) A 2D matrix is generated with random, uniformly distributed, phase values in the interval 0–2π. (b) The matrix is immersed in a larger matrix with zeroed elements. This padding operation is performed to add finite dimension to the speckle spots by increasing the bandwidth of the signal. The ratio between the immersion and immersed matrices is a measure of the number of matrix elements contained (along a linear dimension) inside a speckle. (c) The matrix is Fourier transformed, yielding the field distribution in the far field. (d) The squared modulus of the resulting matrix elements is computed to retrieve the intensity distribution of the speckle pattern.

Fig. S1 shows the optical setup for ISI. Fig. S2 displays the impact of an ISI pulse on fluorescence distribution and how this depends on laser pulse energy. Fig. S3 shows examples of speckles generated in biological samples along the xy and xz planes. Fig. S4 formalizes the ISI process in spectral terms and analyzes the impact of subdiffraction speckle generation on ISI. Fig. S5 shows the statistical scale of ISI speckles compared with the PSF and the impact of decoherence on the fluorescence speckle pattern histogram.

We thank Marin Barisic, Martina Barisic, Danica Drpic, and Eurico Sá for technical help and Flávio P. Ferreira and members of the Chromosome Instability and Dynamics laboratory for thoughtful discussions.

H. Maiato is funded by the seventh framework program grant PRECISE from the European Research Council, FLAD Life Science 2020, and the Louis-Jeantet Young Investigator Career Award.

The authors declare no competing financial interests.

Author contributions: A.J. Pereira conceived the technique and performed the experiments. P. Aguiar and A.J. Pereira performed simulations. A.J. Pereira and M. Belsley developed the ISI theory. A.J. Pereira and H. Maiato designed and performed the biological proof of concept. A.J. Pereira wrote the manuscript with contributions from all authors.