Teams of processive molecular motors are critical for intracellular transport and organization, yet coordination between motors remains poorly understood. Here, we develop a system using protein components to generate assemblies of defined spacing and composition inside cells. This system is applicable to studying macromolecular complexes in the context of cell signaling, motility, and intracellular trafficking. We use the system to study the emergent behavior of kinesin motors in teams. We find that two kinesin motors in complex act independently (do not help or hinder each other) and can alternate their activities. For complexes containing a slow kinesin-1 and fast kinesin-3 motor, the slow motor dominates motility in vitro but the fast motor can dominate on certain subpopulations of microtubules in cells. Both motors showed dynamic interactions with the complex, suggesting that motor–cargo linkages are sensitive to forces applied by the motors. We conclude that kinesin motors in complex act independently in a manner regulated by the microtubule track.
Introduction
Processive molecular motors such as kinesin and dynein hydrolyze ATP to walk on polarized microtubule (MT) tracks in eukaryotic cells. These motors are largely responsible for the trafficking and organization of subcellular cargoes including organelles, vesicles, mRNA particles, and even viruses (Vale, 2003). Defects in intracellular transport have been linked to a range of diseases including neurodegeneration and cancer (Hirokawa et al., 2010; Yu and Feng, 2010). Although the biophysical and biochemical properties of individual motor proteins are well-characterized, the collective behavior of motors is less clear despite evidence that multiple motors are present on a given cellular cargo (e.g., Miller and Lasek, 1985; Ashkin et al., 1990; Snow et al., 2004; Shubeita et al., 2008; Laib et al., 2009; Soppina et al., 2009; Hendricks et al., 2010, 2012). Detailed investigation of this collective behavior is crucial and necessary for understanding transport processes in the cell.
Intuitively, multiple motors are expected to cooperate to generate longer transport distances and sufficient force to pull a bulky cargo through the crowded cytoplasm at efficient speeds. Previous work reconstituting motor–cargo interactions in vitro supported these ideas, showing enhanced run lengths and higher forces for multiple kinesin-1 motors on plastic beads or quantum dots (Block et al., 1990; Vershinin et al., 2007; Beeg et al., 2008; Conway et al., 2012). Theoretical studies using mean-field and Monte Carlo approaches represent ideal motor efficiency and generally agree with these in vitro studies (Klumpp and Lipowsky, 2005; Kunwar et al., 2008). In contrast, recent in vitro studies using precisely defined DNA-based motor assemblies show that the run length enhancements caused by multiple kinesin-1 motors are much smaller than what is predicted by theory, and assemblies of exactly two motors show only a modest run length increase (Rogers et al., 2009; Derr et al., 2012; Furuta et al., 2013). This result has been interpreted as negative interference between kinesin motors (Rogers et al., 2009) that can result in a decrease in motor velocity at very high motor concentrations (Bieling et al., 2008; Conway et al., 2012; Furuta et al., 2013). A load-dependent study of DNA-based motor assemblies showed that although two kinesin-1 motors are capable of generating additional force, they typically only used the action of one motor (Jamison et al., 2010). Thus, any cooperation between kinesin motors remains poorly understood.
Consistent with these recent observations of poor kinesin cooperativity in vitro, the transport of cellular cargoes is largely unaffected by a change in the amount of kinesin-1 (Shubeita et al., 2008; Efremov et al., 2014). However, information regarding multiple motor behaviors in live cells has been difficult to ascertain due to a lack of precise motor number control and the presence of endogenous competing motors (Barlan et al., 2013). Indeed, methods that directly correlate multi-motor behavior in vitro with behavior in cells are lacking. To address these issues, we developed a system for linking protein components with defined spacing and composition in cells. This system is widely applicable to the study of multiprotein assemblies in cells and enables the study of multi-motor transport in a manner that (a) more closely mimics the physiological state of motor–cargo linkages and (b) reveals the influence of cellular architecture on motility events. We first confirmed previous studies with complexes of two kinesin-1 motors and then used the system to study the cooperative behaviors that arise when a slow kinesin-1 motor and a fast kinesin-3 motor are linked in vitro and in live cells. We find that two motors in complex largely function as individual motors that alternate their activities.
Results
Scaffolds and linkers for self-assembly of defined complexes in mammalian cells
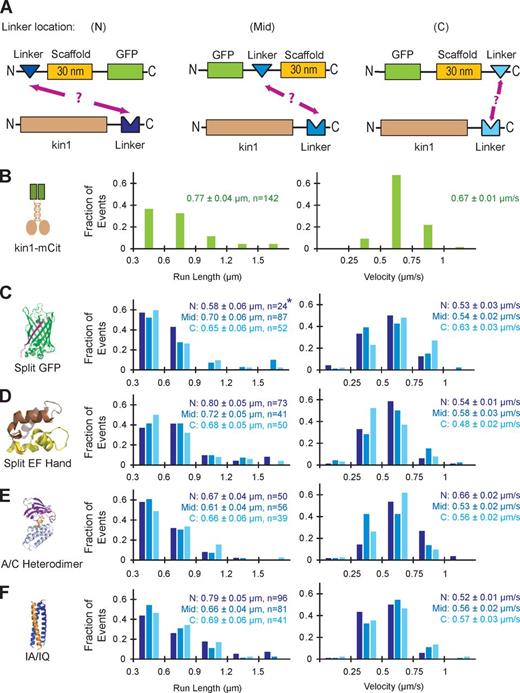
To assemble protein complexes of defined number and spacing in mammalian cells, we developed a biosynthetic system using proteins with well-characterized structural and assembly properties. The basis of our system is a scaffold protein (Fig. 1 A). For this, we chose polypeptides that form a single α helix (SAH) stabilized by ionic interactions between the side chains of alternating glutamate (E) and arginine (R) or lysine (K) residues (thus also called ER/K helices; Knight et al., 2005; Sivaramakrishnan et al., 2008; Baboolal et al., 2009). SAH domains of various lengths are found across phylogenetic kingdoms (Sivaramakrishnan et al., 2008), and we selected helices of 5, 10, 20, and 30 nm (see Materials and methods). Each scaffold also contains a SNAP-tag to enable fluorescent labeling of the scaffold when necessary.
To attach proteins to the scaffold, we selected linker proteins that self-associate (Fig. 1 B). We first tested α-helical protein segments that form coiled-coil structures of defined orientation and oligomeric state. Because our overall goal was to recruit dimeric kinesin motors to a monomeric scaffold, we focused on sequences shown to form trimeric coiled-coils (Fig. S1 A), but heterodimeric or heterotetrameric coiled-coil structures are likely to be more useful in other applications. Specifically, we tested the following coiled-coil sequences: a homotrimeric variant of the leucine zipper from Saccharomyces cerevisiae GCN4 (Holton and Alber, 2004), the homotrimeric coiled-coil domain of mammalian coronin 1 (Kammerer et al., 2005), and de novo designed coiled coils of homotrimeric (Burkhard et al., 2002), homodimeric (Litowski and Hodges, 2002), or heterotrimeric (IA/IQ; Kiyokawa et al., 2004) form (Fig. S1 A). The use of a particular coiled-coil sequence is likely to be context specific, and in our geometry, the heterotrimeric IA/IQ coiled-coil sequence worked best (Fig. 2 F and Fig. S1, A and E), and the other sequences were not pursued further.
We also tested several protein–protein linkers that confer unique advantages to studying macromolecular assembly. We tested a split superfolder GFP (hereafter referred to as split GFP) molecule, which provides a green fluorescent signal upon assembly and an essentially irreversible linkage (Pinaud and Dahan, 2011). We tested the split EF Hand domain from calbindin (Lindman et al., 2009), which assembles with a high affinity (Kd ∼1 nM) that can be increased (Kd ∼1 pM) in the presence of calcium (Lindman et al., 2009). In our system, the tight association of the split EF Hand enables interactions of proteins mixed in vitro. We also tested the drug-inducible dimerization of DmrA (FKBP) and DmrC (FRB domain) upon addition of A/C heterodimerizer (Rapalog-1, AP21967) that has been used to induce dimerization of proteins in cells (DeRose et al., 2013).
To characterize these linkers, we tested their ability to recruit a kinesin-1 motor to a scaffold using two assays: coimmunoprecipitation (Fig. S1, B–E) and single molecule motility assays (Fig. 2). Each linker was tested at three different locations with respect to the scaffold: at the N terminus (N), in the middle (Mid), and at the C terminus (C; Fig. 2 A). For these experiments, we used the 30 nm SAH as a scaffold and a truncated, constitutively active version of the kinesin-1 motor, KIF5C(1–560), hereafter referred to as kin1, as the motor. Coimmunoprecipitation experiments enabled us to verify protein expression and solubility (Fig. S1, B–E, input lanes) as well as the interaction between kin1 and the scaffold by immunoprecipitation with an antibody to kinesin-1 (Fig. S1, B–E, IP:kin1 lanes). The four linkers performed well in these assays with the exception that limited expression was found when the GFP(1–10) component of the split GFP linker was placed at the N terminus of the scaffold (Fig. S1 B, lane 4).
For single molecule motility assays, we placed a fluorescent protein (FP) on the scaffold component such that motility could only be observed when a nonfluorescent kin1 motor was linked to the fluorescent scaffold. Motility was observed for motor–scaffold complexes formed by every linker arrangement (Fig. 2, C–F) except when the N-terminal half of the split EF Hand linker was fused to the C terminus of the scaffold (not depicted). Quantification of the motility events demonstrated that each motor–linker–scaffold complex displayed run length and velocity distributions similar to those of kin1-FP alone (Fig. 2 B). These results demonstrate that our scaffold and linker components have the potential to generate defined multiprotein complexes for analysis in cell lysates.
Verifying multiple protein assembly in live cells
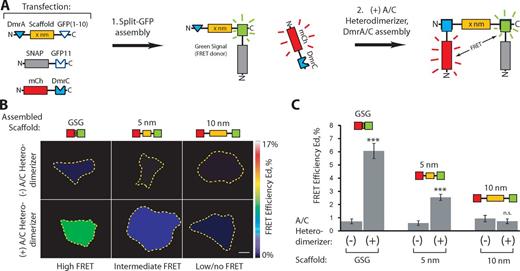
We next verified that the linkers could be used for simultaneous recruitment of two proteins to the same scaffold in cells. To do this, we used Förster resonance energy transfer (FRET) to measure the relative proximity of two scaffold-associated proteins. A superfolder GFP FRET donor was attached to one end of the scaffold via the split GFP linker, and a mCherry FRET acceptor was recruited to the other end of scaffold via the DmrA/DmrC linker system (Fig. 3 A). In the absence of A/C heterodimerizer, little-to-no FRET was observed between scaffold-associated GFP and cytosolic mCherry (Fig. 3, B and C; and Fig. S2 A). Addition of the A/C heterodimerizer caused recruitment of mCherry to the scaffold–GFP complex and a FRET signal that varied with separation distance. The highest FRET efficiencies were obtained for GFP and mCherry separated by a short peptide sequence, moderate FRET was observed for a 5-nm scaffold, and no FRET was observed for a 10-nm scaffold (Fig. 3, B and C; and Fig. S2, A and B). Maximal FRET efficiencies were obtained within ∼45 min of A/C heterodimerizer addition (Fig. S2, C and D).
We also tested whether the scaffold and linker components could be used to create defined multiprotein complexes at specific subcellular locales. The mCherry-DmrC component was enriched at the plasma membrane via a myristoylation-palmitoylation signal (Fig. S3 A) or at the lysosomal surface via fusion to the lysosomal membrane protein Lamp1 (Fig. S3 C). In the absence of A/C heterodimerizer, DmrA–scaffold–split GFP complexes remained cytosolic (Fig. S3, B and D; bottom panels), but addition of A/C heterodimerizer resulted in recruitment to the plasma membrane (Fig. S3 B, top panels) or lysosome (Fig. S3 D, top panels). These results indicate that our scaffold and linker components can be used to generate defined multiprotein complexes in live cells.
Two kinesin-1 motors show minimal cooperation in vitro
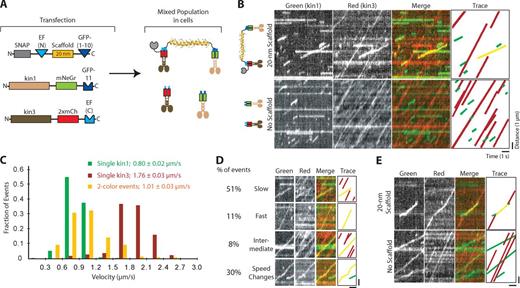
Having verified each linker and scaffold component, we used the system to investigate the cooperative behavior of two kinesin-1 motors attached to the same scaffold. Specifically, we sought to determine whether the nature of the linkage (i.e., our protein assemblies) impacts the cooperative behavior of two kinesin-1 motors. Kin1 motors were labeled with either monomeric Neon Green (mNeGr) or tandem mCherry (2×mCh) FPs, as this pair of FPs was determined to be optimal for two-color single molecule imaging. A kin1-mNeGr motor was recruited to one end of a 20-nm scaffold in cells via the split GFP linker system (providing tandem green FPs), and a kin1-2×mCh motor was recruited to the other end of the scaffold in cell lysates via the split EF Hand linker system (Fig. 4 A). Similar results were obtained using other linker systems (e.g., IA/IQ; see Materials and methods). Motility events were observed by two-color total internal reflection fluorescence (TIRF) microscopy (Video 1) and analyzed using an automated subpixel-resolution tracking routine (Jaqaman et al., 2008) where two-motor events were considered to be trajectories when they overlapped by <1 pixel in the green and red channels.
Single kin1-mNeGr and kin1-2×mCh motors displayed characteristic kinesin-1 motility properties with velocities of 0.74 ± 0.01 µm/s and run lengths of 0.84 ± 0.03 µm (Fig. 4, B–D; Fig. S4, A and B; and Table S1). In the presence of scaffold, complexes containing two kinesin-1 motors on a 20-nm scaffold (colocalized kin1-mNeGr and kin1-2×mCh events) displayed no change in mean velocity but an increase in run length to 1.08 ± 0.04 µm (Fig. 4, B–D; and Table S1). The ∼1.3-fold increase in run length is statistically significant (P < 0.001, two-sample Kolmogorov–Smirnov test [KS test]), and consistent with previous work using DNA-based assemblies (Rogers et al., 2009), but is less than what is predicted from theoretical models (Klumpp and Lipowsky, 2005).
One possible explanation for why two kinesin-1 motors in complex display minimal cooperativity is that geometric constraints limit the MT access of the second motor. Alternatively, as suggested by Driver et al. (2010), both motors may have access to the MT but only one motor is able to effectively engage for motility. In this case, the motility of the assembly is driven by a mixture of one-motor and two-motor states. Consistent with this interpretation, the velocity distribution of the two-motor complexes suggests that the motion is partially driven by two motors (Fig. 4 E). The two-motor events display a tighter distribution of velocities than single motors, as expected, yet the associated decrease in standard deviation is less than the predicted factor of , thus indicating a mixture of states where either one or two motors are engaged (Fig. 4 E; see Materials and methods). To further demonstrate that both motors are geometrically able to engage the MT simultaneously, we examined two-motor motility under limiting ATP conditions (20 µM) in order to increase the pause time of each motor on the MT surface (Xu et al., 2012). We found that two-motor complexes show a substantial increase in run length at limiting ATP (2.6 ± 0.2 µm) relative to single motors (1.10 ± 0.04 µm; Fig. 4, F–H; and Table S1). Together, these data suggest that while two-motor kinesin-1 complexes are capable of coordinating to produce longer runs, the two-motor complexes mostly behave as a single motor under saturating ATP conditions.
The SAH-based scaffolds also allowed us to investigate the influence of separation distance on motor cooperativity (Fig. 5). Interestingly, two motors were better able to cooperate for an increased run length when separated by shorter scaffolds (5, 10, or 20 nm) than when separated by longer scaffolds (30 or 60 nm; Fig. 5, B and D; and Table S1). At the longer separations, no significant increase in run length was observed (P > 0.01, two-sample KS test). Because the shorter scaffolds are more rigid (Sivaramakrishnan et al., 2009), this result indicates that motor cooperativity is enhanced by a rigid connection (see Discussion). Overall, our results suggest that two kinesin-1 motors typically work independently when in complex and neither help nor hinder the partner motor.
A slow and a fast kinesin motor in complex do not cooperate in vitro
We next used our protein-based biosynthetic system to determine the emergent behaviors that arise when two different types of kinesin motors are attached to the same cargo. For this, we paired kinesin-1 with KIF1A, an extremely fast and superprocessive member of the kinesin-3 family (Soppina et al., 2014). Kinesin-1 and kinesin-3 are both essential for neuronal trafficking and are known to cooperate during hyphal growth in Ustilago maydis (Schuchardt et al., 2005; Barkus et al., 2008).
A slow kinesin-1 motor labeled with mNeGr (kin1-mNeGr) was attached to one end of a scaffold using the split GFP linker, and a fast kinesin-3 motor labeled with 2×mCherry (kin3-2×mCh) was attached to the other end using the split EF Hand linker (Fig. 6 A). In the absence of scaffold, green kin1 and red kin3 motors walked independently on the same track with characteristic motility properties (Fig. 6 B and Table S1). Kin1 motors displayed a mean velocity of 0.80 ± 0.02 µm/s and mean run length of 0.74 ± 0.02 µm, whereas kin3 displayed significantly higher mean velocity (1.76 ± 0.03 µm/s) and run length (7.9 ± 0.2 µm; Fig. 6 C and Table S1). In the presence of scaffold, the two-motor events exhibited a mean velocity of 1.01 ± 0.03 µm/s (Fig. 6 C and Table S1), which suggests that the motors coordinate their motilities to generate intermediate speeds. However, careful dissection of the individual motility events revealed diverse behaviors not compatible with motor coordination (Fig. 6 D; additional examples are given in Fig. S4 C). 51% of the two-motor events were classified as slow, as their velocities matched those of single kin1 motors, whereas 11% of the two-motor events were classified as fast, as their velocities matched those of single kin3 motors (Fig. 6 D and Table S1). Only 8% of the two-motor events displayed intermediate velocities. The remaining 30% of the two-motor events exhibited alternating periods of slow and fast movement (Fig. 6 D), which suggests a possible alternating action mechanism between kin1 and kin3. Interestingly, although kinesin-3 motors have a higher affinity for MTs than kinesin-1 motors (Woehlke et al., 1997; Soppina and Verhey, 2014), kin1 appears to dominate two-motor motility in vitro, which suggests that it can act as a brake to slow down overall velocity. These results support the conclusion that kinesin motors in complex work independently and additionally show that the motors can “take turns” or alternate their activities.
Two-motor complexes containing a slow kin1 motor and a fast kin3 motor also engaged in interesting merging and splitting behaviors. In 11% of all two-motor events, kin1 and kin3 motors were observed to move independently before merging and moving together on the MT (Fig. 6 E and Video 2). In 21% of all two-motor events, the complexed kin1 and kin3 motors split apart and continued as individual motors (Fig. 6 E). Merging and splitting behaviors were not observed for two kinesin-1 motors present on the same scaffold (Fig. 4), which suggests that these behaviors are due to slow and fast motors influencing each other’s motility. The majority of the splitting events (74%) were preceded by a period of slow velocity. We speculate that as the slow kin1 motor moves processively, the fast kin3 motor is attempting to engage with the track, and when it does, it exerts a force that results in dissociation of the motor–scaffold linkage.
Two-motor complexes behave in a track-dependent manner in COS7 cells
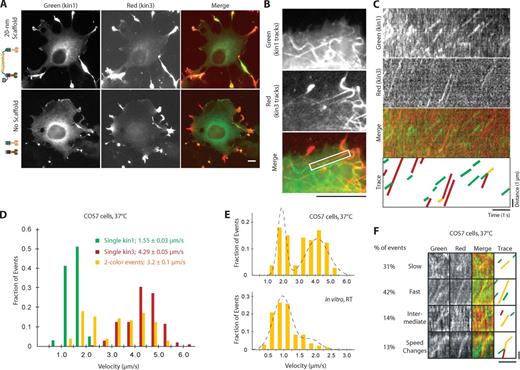
A major advantage to our protein-based approach is the potential to assemble two-motor complexes and track their behavior in live cells. After overnight expression, kin3-2×mCh motors accumulated at the plus ends of MTs in the cell periphery, presumably because of their superprocessivity (Soppina et al., 2014), whereas the moderately processive kin1-mNeGr motors were more diffusely distributed (Fig. 7 A, no scaffold). In the presence of scaffold, kin1 was redistributed to the cell periphery due to the activity of the associated kin3 motor (Fig. 7 A), providing validation of two-motor assembly at high expression.
To resolve individual motility events in live cells, we limited protein expression to 4 h before TIRF imaging (Cai et al., 2009). Even at low expression levels, kin3 motors and linked kin1+kin3 motors accumulated at the plus ends of MTs in the cell periphery, making it difficult to track motility events along cytoplasmic MTs. We thus released individual kin3 and linked kin1+kin3 motors into the cytoplasm by treating cells with the MT-depolymerizing agent nocodazole (NZ) for 5 min before imaging (Fig. S5 A). To analyze motility events (Video 3), we generated standard deviation (SD) maps (Cai et al., 2009) to locate MTs (Fig. 7 B) and then generated kymographs along each track (Fig. 7 C). Two-motor complexes moved at a mean velocity of 3.2 ± 0.1 µm/s, which falls roughly between the individual motor velocities of 1.55 ± 0.02 µm/s for kin1 and 4.29 ± 0.05 µm/s for kin3 at 37°C in live cells (Fig. 7 D and Table S1). Analysis of individual two-motor motility events revealed that the mean intermediate velocity was due to the linked kin1 and kin3 motors acting independently. Similar to in vitro, we observed four types of two-motor behavior in live cells: slow (31%), fast (42%), intermediate (14%), and changes (13%) in velocity (Fig. 7 F and Fig. S5 B). That the majority of two-motor events in cells display fast kin3-like velocities (Fig. 7 F) was surprising given the dominance of slow kin1-like events in vitro (Fig. 6 D). The dramatic shift in kin3 engagement can be seen in the velocity distributions for two-motor complexes in live cells, which now appear bimodal and are best fit by a two-peaked Gaussian distribution (Fig. 7 E). These findings show that slow kin1 and fast kin3 motors in a two-motor complex behave as individual motors in cells and that kin1 is unable to dominate the motility behavior.
We hypothesized that the relative ability of either kin1 or kin3 to dominate two-motor motility events is influenced by the MT itself. Our previous work demonstrated that kinesin-1 motors are selective in cells and prefer to move along the stable MTs marked by posttranslational modifications, whereas kinesin-3 motors are nonselective and use all MTs for motility (Cai et al., 2009). We thus predicted that the motors would engage equally with the stable MTs, whereas kin3 motors would be better able to engage on dynamic MTs. To test this, we treated cells with NZ at times and concentrations that selectively enrich specific subsets of MTs (Piperno et al., 1987). Treatment of cells with low levels of NZ results in enrichment of stable, modified MTs (Fig. 8 A, middle). In this case, the behavior of the two-motor complexes was not changed in terms of mean velocity (3.1 ± 0.2 µm/s; Fig. 8 B, middle; and Table S1) or the proportion of slow kin1-like (31%) and fast kin3-like (43%) events observed (Fig. 8 C). Thus, both kin1 and kin3 motors are able to effectively engage and drive motility of the complex on stable, modified MTs.
Treatment of cells with high levels of NZ depolymerizes nearly all MTs, and NZ washout enables the examination of motility events on newly grown (nascent) MTs (Fig. 8 A, bottom). Under these conditions, the velocity distribution of the two-motor events was again fit by a two-peaked Gaussian but with an increase in the mean velocity of two-motor complexes (3.4 ± 0.2 µm/s; Fig. 8 B, bottom; and Table S1). Importantly, a dramatic decrease in the number of slow kin1-like motility events was observed under these conditions (from 31% to 14%; Fig. 8 C). These results suggest that kin3 can dominate motility events under conditions where kin1 displays a decreased affinity for the MT track. We conclude that the slower kin1 motor typically dominates two-motor motility events. This is observed both in vitro on homogeneous MTs and in cells on stable MTs. The fast kin3 motors are only able to dominate motility events in cells on the dynamic population of MTs, which kin1 does not prefer.
Discussion
We describe a new method for assembling multiprotein complexes of defined composition and geometry in mammalian cells that is broadly applicable to studying cellular signaling, motility, and organization. We apply this assembly method to compare, for the first time, the cooperative behavior of two-kinesin complexes in vitro to that in live cells. We find that two kinesin motors in complex act independently (do not help or hinder each other) and that they can alternate their activities. For complexes containing a fast and a slow kinesin motor, the outcome in cells is a bimodal distribution of fast and slow velocities that is influenced by the state of the MT track where the motility event takes place. In cells and in vitro, we find that the protein–protein attachments between motor and scaffold are dynamic and that the force exerted by one motor can result in dissociation of the complex.
Our finding that assemblies of two kinesin-1 motors display a small but significant 1.3-fold increase in run length relative to single motors generally agrees with previous in vitro studies that showed a 1.3- to 2.7-fold increase in run length for two kinesin-1 motors assembled on a DNA scaffold or attached to antibodies (Rogers et al., 2009; Derr et al., 2012; Xu et al., 2012; Furuta et al., 2013). The fact that these experimentally derived increases in run length fall short of the predicted theoretical values (Klumpp and Lipowsky, 2005) suggests that multi-motor complexes are influenced by a factor not replicated in the modeling. One component likely to influence the ability of kinesin motors to coordinate their motion is the stiffness of the linkage. A more rigid connecting element could be beneficial to multiple motor coordination by allowing motors to effectively communicate via long-range force transduction. Indeed, the largest increases in run length for two kinesin-1 assemblies have been found in rigid DNA assemblies (Derr et al., 2012; Furuta et al., 2013), whereas more flexible assemblies have resulted in less cooperativity (this study and Rogers et al., 2009). In addition, we found that increasing the length of our scaffold, which effectively decreases the rigidity of the connecting element, dampens the cooperative effect on run length (Fig. 5). A fluid linkage between motors, such as the lipid bilayer of a vesicular cargo, would then be expected to result in no cooperativity; indeed, recent work in cells demonstrated that motor number does not impact the run length of cargoes such as lipid droplets or peroxisomes (Shubeita et al., 2008; Efremov et al., 2014).
Our work provides the first analysis of the emergent behaviors that arise when plus-end–directed kinesin motors with different motility properties are attached to the same cargo, in this case a SAH scaffold. We find that two-motor assemblies comprised of a slow kinesin-1 motor and a fast kinesin-3 motor rarely move with intermediate velocities, in contrast to previous work where mixtures of slow and fast motors displayed intermediate velocities in MT gliding assays (Pan et al., 2006; Bieling et al., 2010). These findings highlight the importance of investigating population behaviors at the single molecule level. Analysis of individual events in vitro demonstrated that, of all two-motor events, most (62%) displayed either kin1-like (51%) or kin3-like (11%) motility properties rather than an intermediate velocity (8%). In addition, 30% of the two-motor events were observed to change speed while in motion, alternating between slow kin1-driven motility and fast kin3-driven motility. These results suggest an alternating action mechanism in which only one motor is active at a time.
A major advantage to our protein-based assembly method is the ability to study molecular behavior within the cellular environment. Indeed, we directly compared the motility of kin1+kin3 complexes in vitro to that in live cells. We found that the slow kin1 motor dominates the motility events in vitro on homogeneous MTs, whereas the fast kin3 motor can dominate the motility events in cells where the heterogeneous MT network provides MT tracks that are not used by kin1. These findings emphasize that studying intracellular trafficking events in cells reveals emergent properties that cannot be ascertained from in vitro assays.
Single molecule analysis also revealed dynamic merging and splitting behaviors for fast and slow motors in complex. Such merging and splitting behaviors were not observed for complexes containing two kinesin-1 motors, which suggests that this is a novel behavior that arises when motors with different velocities are present on the same scaffold. The majority of the splitting behaviors (74%) occurred after periods of slow transport. We interpret this to mean that if the fast kin3 motor engages with the MT during a motility event driven by the slow kin1 motor, then kin3 generates an internal force on the two-motor complex that results in dissociation of the motor–scaffold complex. Our observation of such dynamic behaviors is likely caused by our use of more physiological protein–protein linkages between the motors and the scaffold. By modeling the 20-nm SAH scaffold as a wormlike chain (WLC) using the published SAH persistence length (Sivaramakrishnan et al., 2009), we predict that the SAH exerts a restoring force of 2–4 pN as it approaches its maximum extension (see Materials and methods). The magnitude of this force is less than the stall force of either motor (Svoboda and Block, 1994; Tomishige et al., 2002) and is comparable to the rupture force of noncovalent protein–protein interactions (Weisel et al., 2003). We believe the most likely scenario underlying the splitting of slow and fast motor complexes is the dissociation of the split EF Hand linker, as the split GFP linkage is essentially irreversible (Pinaud and Dahan, 2011). Unless motor–cargo attachments in cells are strengthened by additional mechanisms, it seems likely that similar forces could cause motors to dissociate from their cargoes during motility events.
Collectively, our results indicate that kinesin motors present on the same scaffold or cargo typically do not coordinate their activities but rather act independently and can alternate their activities. What then is the functional output of attaching several motors to a cellular cargo? We can envision two outputs of multi-motor cooperativity that are critical for motor-driven transport in cells. First, multiple kinesins can work together to increase force generation under applied loads. Indeed, multiple kinesin-1 motors cooperate to maintain motor velocity when pulling against a viscous drag (Gagliano et al., 2010; Jamison et al., 2012) and are required to generate sufficient force for tube formation (Leduc et al., 2004; Campàs et al., 2008). Second, the presence of multiple motors may enable the cargo to avoid traffic jams or navigate around obstacles on the MT track (Ross et al., 2008; Schroeder et al., 2010).
The protein-based assembly system we developed can be used to generate higher-order motor complexes; e.g., teams of three or more kinesin motors in a variety of geometric arrangements. The system will also be useful to probe the functional output of kinesin stalk and tail domains by using full-length motors as well as light chains and other associated proteins, especially in combination with RNAi inhibition or mutagenesis approaches. Furthermore, this assembly system can be used to study not just multiple kinesin motors, but the interplay of kinesins with dynein and myosin motors. Recent studies indicate that kinesin and dynein motors in complex engage in a tug-of-war or codependence when present on cellular organelles (Hancock, 2014) and that teams of processive myosin motors can cooperate both in vitro and in live cells (Lu et al., 2012; Efremov et al., 2014; Hariadi et al., 2014). The methods we have developed will be useful to understand how the mechanical properties of each motor allow it to influence and be influenced by other motors in complex. Additionally, the tools developed here will be useful for studying other cellular processes that require the assembly of defined macromolecular structures such as signaling pathways and intracellular transport events.
Materials and methods
Plasmids
Constitutively active versions of the kinesin-1 motor rat KIF5C (aa 1–560) and the kinesin-3 motor rat KIF1A (aa 1–393 with the leucine zipper dimerizing segment of GCN4) have been described previously (Cai et al., 2007, 2009; Soppina et al., 2014). DNA fragments encoding SAH domains of various lengths were generated by PCR cloning of the relevant sequences: a 5-nm helix from Homo sapiens translation initiation factor IF-2; a 10-nm helix from Sus scrofa Myosin VI medial tail; a 20-nm helix from S. cerevisiae mannosyltransferase MNN4; and a 30-nm helix from Trichomonas vaginalis Kelch-motif family protein (Sivaramakrishnan et al., 2008, 2009). The 60-nm helix is a tandem repeat of 30-nm helices separated by four tandem Gly-Ser-Gly (GSG) sequences. Multiple GSG repeats were also included between all scaffold and linker components to ensure flexibility and rotational freedom of each component. IA/IQ fusions were generated by insertion of oligonucleotides encoding the peptides. Plasmids encoding FKBP and FRB were obtained from ARIAD Pharmaceuticals and are now available from Takara Bio Inc. as DmrA and DmrC, respectively. Plasmids encoding mNeonGreen were obtained from Allele Biotechnology. EF Hand and tandem mCherry sequences were synthesized (DNA 2.0). Plasmids encoding split superfolder GFP components were a gift from F. Pinaud (University of Southern California, Los Angeles, CA). Each component was subcloned behind the cytomegalovirus promoter in the EGFP-N1 vector (Takara Bio Inc.); this vector also contains an SV40 origin for replication in mammalian cells and a kanamycin resistance cassette for amplification in Escherichia coli. All plasmids were verified by DNA sequencing.
Cell culture, transfection, Western blotting, and immunofluorescence
COS cells were cultured, transfected, and lysed as described previously (Cai et al., 2007; Soppina et al., 2014). For immunoprecipitation, lysates were incubated with antibodies for 3 h at 4°C, Protein A agarose beads were added for an additional 30 min at 4°C, and the immunoprecipitates were analyzed by blotting with a monoclonal antibody to bovine brain kinesin-1 (Mouse MAb1614; EMD Millipore) or a polyclonal antibody raised in rabbits against a GFP peptide (antigen sequence CFKEDGNILGHKLE). For immunoprecipitation experiments using DmrA/C linkers, 20 ng/ml rapamycin (EMD Millipore) was added 1 h before lysis and maintained throughout lysis and immunoprecipitation. For immunofluorescence, monoclonal antibodies to total β-tubulin (Mouse E7; Developmental Studies Hybridoma Bank) and acetylated α-tubulin (Mouse 6-11B-1, #T7451; Sigma-Aldrich) were used.
FRET stoichiometry
Fluorescence images of live COS7 cells were collected at 37°C in Leibovitz’s L-15 medium without phenol red (Life Technologies) using an inverted microscope (IX70; Olympus) with a 40× objective lens (LCPlan Fl, NA 0.6, 1.5× tube lens) and an X-Cite 120 metal halide light source (EXFO). For DmrA/C FRET experiments, A/C heterodimerizer (Takara Bio Inc.), equivalent to Rapalog-1 AP21967 (ARIAD Pharmaceuticals) was added at 500 nM for 60 min unless otherwise noted. Fluorescence excitation and emission wavelengths were selected using a DAPI/FITC/Tx Red filter set (Chroma Technology Corp.) and a Lambda 10-3 filter wheel controller (Sutter Instrument) equipped with a shutter for epifluorescence illumination control. Images were recorded with a CoolSNAP HQ2 14-bit charge-coupled device (CCD) camera (Photometrics). Image acquisition was performed using MetaMorph (Molecular Devices), and FRET values were calculated using the MATLAB-based (The MathWorks) program FRET calculator (http://sitemaker.umich.edu/4dimagingcenter/fret_calculator). FRET microscopy and analysis was performed using equations described in Hoppe et al. (2002) as follows. Each collected image was corrected for uneven illumination shading by collecting flat-field shade images from a fluorescent cover glass and normalizing by these values. Images were then corrected for pixel bias offset by collecting images with the excitation light blocked and normalizing by these values. In order for the FRET stoichiometry equations to be used, the FRET microscope was then calibrated to obtain the parameters α, β, γ, and ξ, which describe the baseline fluorescence contributions from each fluorophore in each channel for the imaging filter set (see Hoppe et al., 2002). These parameters were calculated from COS7 cells expressing mCherry alone (α), superfolder GFP alone (sfGFP; β), or an mCherry-sfGFP molecule linked by 12 aa (γ and ξ). sfGFP was used in calibrations to allow proper comparison to the split superfolder GFP used in protein assembly. For the baseline FRET efficiency parameter used in calculations of γ and ξ, we used the previously reported value from Khmelinskii et al. (2012), where FRET efficiency for the sfGFP-mCherry pair was determined by fluorescence correlation spectroscopy (FCS) measurements using recombinant proteins. For each cell, the background-subtracted, bias/shade-corrected mean values of the donor (sfGFP ex/em), acceptor (mCherry ex/em), and FRET (sfGFP ex, mCherry em) images were used in all calculations. Mean values of the apparent FRET efficiency relative to acceptor (EA) and donor (ED) fluorescence and for the molar ratio of acceptor to donor (R) were then calculated using FRET stoichiometry equations (Hoppe et al., 2002) for each cell:
where IF, ID, and IA are the fluorescence intensities in the FRET, donor, and acceptor channels, respectively. Reported values are averages of all pixels inside the cell, where phase images were used to draw an outline of the cell periphery. Only cells with a molar ratio (Rm) <2.5 were considered. A two-tailed t test was used to compare steady-state ED values from n ≥ 31 cells from three independent experiments for each data point.
Characterization of linkers by single molecule motility assays
Nonfluorescent kin1 motors and GFP-labeled scaffolds (Fig. 2 A) in lysates containing 2 mM ATP were diluted in P12 buffer (12 mM Pipes/KOH, 1 mM EGTA, and 2 mM MgCl2, pH 6.8). 5 µl of each lysate was added to flow chambers containing taxol-stabilized MTs (Cytoskeleton, Inc.) and 45 µl of oxygen scavenger buffer (1 mM DTT, 1 mM MgCl2, 2 mM ATP, 10 mM glucose, 0.1 mg/ml glucose oxidase, 0.08 mg/ml catalase, 10 mg/ml BSA, and 10 µM taxol in P12). Linker screening assays (Fig. 2) were performed at the Single Molecule Analysis in Real Time (SMART) Center at the University of Michigan (Ann Arbor, MI). Images were acquired at room temperature using a microscope (IX-81; Olympus) with a 60× 1.49 NA oil immersion TIRF objective with a 4× tube lens (Olympus), equipped with five fiber-coupled lasers (405 nm, 488 nm, 532 nm, 561 nm, and 640 nm) and independently focused via Cell^TIRF module (Olympus). Individual mCitrine-labeled motors (Fig. 2 B) or GFP-labeled scaffolds (Fig. 2, C–F) were excited at 488 nm with 100-ms exposure, and images were collected via an EM CCD detector (iXon 897, 512 × 512, 16 µM array; Andor Technology). For linker screening assays, the SpotTracker plugin for ImageJ (Sage et al., 2005; http://bigwww.epfl.ch/sage/soft/spottracker/) was modified to batch-process motility data (Cai et al., 2009) and used to calculate the speed and run length.
In vitro single molecule motility assays
Motor proteins in lysates containing 20 µM ATP (low ATP condition) or 2 mM ATP (saturating ATP condition) were added to flow chambers in P12 buffer (12 mM Pipes/KOH, 1 mM EGTA, and 2 mM MgCl2, pH 6.8). To drive in vitro complex formation via split EF Hand linkages (Fig. 4 A), 5 µl of each lysate was incubated for 10 min on ice in the presence of 1 mM CaCl2, and 1–5 µl of this mixed lysate was used for subsequent imaging. In all other motility assays, 0.5–5 µl of lysate was added directly to flow chambers containing HiLyte-647–labeled, taxol-stabilized MTs (Cytoskeleton Inc.) and 45 µl of oxygen scavenger buffer (1 mM DTT, 1 mM MgCl2, 20 µM or 2 mM ATP, 10 mM glucose, 0.1 mg/ml glucose oxidase, 0.08 mg/ml catalase, 10 mg/ml BSA, and 10 µM taxol in P12). Motility assays (Figs. 4–8) were performed at room temperature using a microscope (Ti-E/B; Nikon) with a 100× 1.49 NA oil immersion TIRF objective with a 1.5× tube lens (Nikon) equipped with three 20-mW diode lasers (488 nm, 561 nm, and 640 nm) combined into a single fiber and rapidly controlled with an acousto-optic tunable filter (AOTF; Agilent Technologies). Images were collected via an EMCCD detector (iXon X3 DU897, 512 × 512, 16 µM array; Andor Technology). For near simultaneous, two-color imaging, the microscope was modified to include a dual-band laser polychroic mirror (ZT488/561rpc; Chroma Technology Corp.), a dual-band sputtered emission filter (ZET488/561m; Chroma Technology Corp.), and a dual-band sputtered clean-up filter (ZET488/561×; Chroma Technology Corp.), and the AOTF was used to rapidly switch between 488 nm (2 mW power) and 561 nm (4 mW power) laser excitation with 50-ms exposures in each channel. Images were acquired continuously in saturating ATP and at 1 Hz for limiting ATP. Two-color colocalized events were defined as events that were separated by <1 pixel in both x and y for at least 20% of the event lifetime. To avoid possible tracking differences arising from different fluorescence properties, only the run length and velocity values from the 488-nm channel are reported.
Analysis of complexes containing two kinesin-1 motors in vitro
For analysis of kinesin-1 motility events (Figs. 4 and 5), movies were converted to TIF stacks using ImageJ, and a standard deviation projection map (Image → Stack → Z Project) was created to generate a map of the MT tracks. MATLAB tracking software (Jaqaman et al., 2008) was used to automatically generate single-particle trajectories. This method uses a global optimization algorithm to generate complete trajectories of single particles even if particle signal is temporarily lost due to high background or signal loss. Default software parameters were used, except that a rolling window time average of three frames and a Gaussian mixed-model fit (10 iterations, α = 0.05) were used to determine the subpixel location of particles. For particle tracking, the maximum gap to be closed was one frame, the minimum length of each connected trajectory was two frames, and parameters for directed motion with no diffusion were used. Only trajectories lasting at least five frames were considered. Nonprocessive trajectories were eliminated by classifying each event as linear or random based on the asymmetry in the scatter of particle positions along each trajectory, and keeping only linear events (Huet et al., 2006; Jaqaman et al., 2008). For two-color experiments, each channel (488 nm and 561 nm) was analyzed separately and the final trajectories were compared.
In the absence of scaffold, only 4.2% of kin1-mNeGr and kin1-2×mCh events were found to colocalize in the green and red channels, whereas more colocalized events were observed in the presence of scaffold (e.g., Fig. 5 B). Complete multiprotein assembly is apparently limited by the dilute conditions of our assays. All four linkers (Fig. 1 B) were able to assemble kinesin motors on SAH scaffolds and resulted in similar motility properties for two-kin1 complexes. Two-motor complexes assembled using the split GFP and the split EF Hand linkers showed a higher percentage of two motors in complex (colocalized kin1-mNeGr and kin1-2×mCh) than for complexes assembled via the IQ/IA or DmrA/C linkers, presumably because of their higher affinities and the irreversible nature of the split GFP association. Thus, the split GFP and split EF Hand linkers were used for all two-motor assemblies reported in this study. The percentage of two-color events was also higher for shorter scaffolds (5, 10, or 20 nm), likely because of their higher expression levels (Fig. 5 B).
To analyze the contribution of one- versus two-motor motility events to the population (Fig. 4 E), we assume that each motor independently has an identical mean velocity µ and standard deviation σ, with an associated probability distribution function (PDF):
If two kinesin-1 motors are simultaneously bound to the MT, then the observed velocity distribution of the two-motor complex will be described by a PDF (blue line in Fig. 4 E) that is a combination of the two independent normal distributions with a standard deviation smaller than that of a single kinesin-1 motor by a factor of , as predicted by the central limit theorem.
If only one motor engages the MT at a time, then the PDF should resemble that of a single motor (green line in Fig. 4 E). The experimentally derived probability distribution for two kinesin-1 motors in complex (yellow dotted line in Fig. 4 E) falls in between these values. To determine the proportion of events driven by an individual motor in the complex, the observed two-motor standard deviation σ2 was fit by
where α, a value that falls between 0 and 1, is the proportion of the single-motor contribution. The limits of α are defined by the fact that at α = 0, two-motor events are driven by both motors (blue line in Fig. 4 E), and when α = 1, two-motor events are driven by only one of the motors (green line in Fig. 4 E). We find that α = 0.35 best describes the experimental data (yellow line in Fig. 4 E). Experimental data in Fig. 4 E excludes data using the 30-nm SAH, which showed a significant decrease in mean velocity (Fig. 5).
Analysis of complexes containing a kinesin-1 and a kinesin-3 motor in vitro
For analysis of kin1+kin3 motility events (Figs. 6–8), the high velocity of kin3 and the relatively weak signal of mCherry prevented analysis using the automated tracking routine. Instead, kymograph analysis was used. Maximum intensity projections were generated to determine the location of MTs, and kymographs were generated (width = 5 pixels) along these tracks using Elements (Nikon) for measuring run lengths and velocities. Only events of at least five frames (500 ms) were considered. For two-color, two-motor events, the reported velocity and run length values are only for segments where red and green trajectories overlap. Slow events were defined as two-motor events with a velocity slower than the mean + 1 SD of kin1 alone. Fast events were defined as two-motor events with a velocity faster than the mean − 1 SD of kin3 alone. Intermediate events were defined as two-motor events with a velocity between these thresholds. Speed-changing events were defined as two-color events with at least two discrete velocity segments (>5 frames for each velocity).
Cumulative distribution functions (CDFs)
CDFs of velocities and run lengths were generated via MATLAB, and mean values were obtained as described previously (Thorn et al., 2000). CDFs were used for statistical analysis because they are continuous and do not introduce any subjective binning. To obtain mean run length values, run length distributions were first reorganized into a CDF with the built-in MATLAB function ecdf, then the lsqcurvefit function was used to generate a least squares fit of the experimental CDF to the hypothetical distribution from x0 to infinity, where x0 is the minimum run length of 0.3 µm (run length values <0.3 µm were deleted from the run length CDF):
where the decay constant t is the only fitted parameter. The mean run length for the distribution is then defined by adding the minimum run length x0 to the decay constant. Errors were estimated by the bootstrap technique (Thorn et al., 2000) by using the MATLAB function bootfunc for resampling. Each distribution was resampled 200× and refit to this CDF equation. The standard deviation of the bootstrap distribution for the resampled datasets was taken as the error for each fitted quantity.
Mean velocity values were obtained in an identical way, only no minimum velocity was defined. Velocity CDFs were fit to the hypothetical CDF for a normal distribution using a nonlinear least squares fit with free parameters µ (mean) and σ (standard deviation):
Two-peaked Gaussian fits in Figs. 7 and 8 were obtained by fitting velocity CDFs to the hypothetical CDF for the sum of two normal distributions using a nonlinear least squares fit with free parameters µ1 (mean of peak 1), σ1 (standard deviation of peak 1), µ2 (mean of peak 2), σ2 (standard deviation of peak 2), and ϕ (relative contribution of peak 1, value between 0 and 1):
Broken lines in Figs. 7 E and 8 B were obtained by plotting the PDF of the sum of two Gaussians with the parameters obtained from this CDF fit, and comparing to the binned data histogram:
Live cell two-color single molecule assays and kymograph analysis
Live cell TIRF assays (Figs. 7 and 8) were performed as described previously (Cai et al., 2009). COS7 cells on a glass-bottomed dish (MatTek Corporation) were imaged at 37°C by TIRF microscopy (see “In vitro single molecule motility assays”) at 25-ms exposures for each channel. Although 4–8 h after transfection was optimal for detecting single kinesin motors in the crowded cellular environment (Cai et al., 2007), we found that very few two-motor complexes formed in this time period. Thus, cycloheximide (100 µg/ml; #94271; AMRESCO) was added to and maintained in the cell culture media starting at 4 h after transfection to retain low protein expression but allow complex formation. For imaging, cells were treated with NZ, and washed three times in DMEM, then images were collected at 37°C in Leibovitz’s L-15 medium without phenol red (#21083-027; Life Technologies). Standard deviation maps were generated using ImageJ to show the location of motility events in cells. To decrease autofluorescence background and quantify motility events, the minimum intensity projection was subtracted from each pixel, and then maximum intensity projection maps and kymographs were generated (max width = 5 pixels) along these tracks (Elements; Nikon). Two-color events were defined as processive, unidirectional events that colocalized within 1 pixel for at least three consecutive frames. Only continuous, stationary tracks were considered in subsequent analysis. Kymograph analysis was performed as described for kinesin-1 + kinesin-3 motors in vitro. Slow, fast, and intermediate events were defined as for analysis of in vitro events. Speed-changing events were two-color events with at least two easily discrete velocity segments (>3 frames).
Wormlike chain modeling
To determine how much force is felt by each motor as both motors are engaged with the MT, we modeled the scaffold as a wormlike chain approximation where the contour length L0 (end-to-end distance at full extension) and persistence length P (related to stiffness) are defined (Marko and Siggia, 1995):
Because most experiments were performed with a 20-nm scaffold, we used contour length L0 = 20 nm. Based on previous studies of the SAH (Sivaramakrishnan et al., 2009), we used a persistence length P = 15 nm. Using this model, we predict the motors will feel an internal force of 2.4 pN when the end-to-end separation of the helix is 16 nm, with the internal force rapidly increasing as a function of end-to-end separation.
Online supplemental material
Fig. S1 lists coiled-coil linkers and shows coimmunoprecipitation experiments to validate the use of IA/IQ, split GFP, split EF Hand, and FKBP/FRB linkers. Fig. S2 shows representative raw images from FRET analysis and a time course of FRET upon addition of A/C heterodimerizer. Fig. S3 shows that the scaffolds and linkers can be used to assemble multiprotein complexes at specific subcellular locales. Fig. S4 shows motility data for two kinesin motors in vitro. Fig. S5 shows motility data for kin1+kin3 motors in live cells. Table S1 lists a summary of the motility data in this study. Video 1 shows time-lapse TIRF imaging of complexes containing two kin1 motors in vitro. Video 2 shows time-lapse TIRF imaging of complexes containing kin1+kin3 motors in vitro. Video 3 shows time-lapse TIRF imaging of complexes containing kin1+kin3 motors in live COS7 cells.
Acknowledgments
We thank members of the Verhey laboratory for help and discussions. We thank Sam Straight and the Center of Live Cell Imaging for help with FRET. We thank F. Pinaud for the gift of split superfolder GFP plasmids. We thank the Single Molecule Analysis in Real-Time Center of the University of Michigan (seeded by National Science Foundation MRI-R2-ID award DBI-0959823).
This work was supported by grants to K.J. Verhey (National Institutes of Health [NIH], National Institute of General Medical Sciences RO1070862) and S. Sivaramakrishnan (NIH 1DP2 CA186752-01).
The authors declare no competing financial interests.
Author contributions: S.R. Norris, V. Soppina, D. Cai, and K.J. Verhey designed the research. S.R. Norris, V. Soppina, A.S. Dizaji, and K.I. Schimert performed the research. A.S. Dizaji, D. Sept, and S. Sivaramakrishnan contributed new reagents or analytic tools. S.R. Norris and A.S. Dizaji analyzed data. S.R. Norris and K.J. Verhey wrote the paper with input from all authors.