Nuclear envelope morphology constrains diffusion and promotes asymmetric protein segregation in closed mitosis

Asymmetric cell division is a major mechanism for the generation of cell diversity in eukaryotes, particularly through unequal segregation of cell fate determinants between daughter cells. Asymmetric cell division is a two-step process. First, the cell polarizes its cortex and accumulates fate determinants to one pole of the cell. Second, the mitotic spindle aligns with the cell polarity axis, defining the division axis of the cell. This places the polarized material on one side of the future division plane and, therefore, in only one of the two daughters. Subsequently, the asymmetrically segregated cell fate determinants specify the cell’s identity and drive differentiation from its sister.

Several transcription factors, such as Prospero in Drosophila melanogaster, Pie-1 in Caenorhabditis elegans, and Ash1 in budding yeast, also segregate asymmetrically despite their nuclear localization (Spana and Doe, 1995; Bobola et al., 1996; Mello et al., 1996; Sil and Herskowitz, 1996). To allow this asymmetry, Prospero and Ash1 exit the nucleus before division and relocalize to the cell cortex, similarly to the other fate determinants (Spana and Doe, 1995; Long et al., 1997; Takizawa et al., 1997; Broadus et al., 1998; Schuldt et al., 1998).

The transcription factor Ace2, however, does not appear to use this mechanism. This protein, which contributes to the asymmetry of budding yeast division, accumulates specifically in the nucleus of the bud. Indeed, yeast cells divide by budding of a future daughter cell off the surface of the original mother cell. By inducing transcription of several daughter-specific genes, Ace2 triggers many aspects of daughter-specific transcription and governs the physical separation of the newborn cell from its mother after completion of cytokinesis (Dohrmann et al., 1992; Spellman et al., 1998; Colman-Lerner et al., 2001).

Unlike Prospero and Ash1, Ace2 localizes fully symmetrically to the cytoplasm throughout mitosis (Dohrmann et al., 1992). Indeed, Ace2 asymmetry is established at the level of nuclear import/export, before cytokinesis (Dohrmann et al., 1992; O’Conallain et al., 1999; Colman-Lerner et al., 2001; Weiss et al., 2002; Mazanka et al., 2008). Ace2 enters both mother and daughter nuclei but efficiently exits the nucleus located in the mother cell and not its counterpart in the bud (Mazanka et al., 2008; Mazanka and Weiss, 2010). Retention in the daughter part of the nucleus in late mitosis is facilitated through Ace2 phosphorylation by the LATS-related kinase Cbk1, the downstream effector of the regulation of Ace2 and morphogenesis (RAM) network (Weiss et al., 2002; Mazanka et al., 2008; Pan, 2010).

Here, we show that the asymmetric distribution of Ace2 in the nucleus precedes karyofission. Using photobleaching techniques and spatial stochastic modeling and simulations, we investigated the mechanisms allowing Ace2 accumulation specifically in one half of the nucleus.

To determine when Ace2 asymmetry is established relative to nuclear division, we followed Ace2-GFP using live-cell fluorescence microscopy. We visualized nuclear shape using the reporter protein dsRed-HDEL, which localizes to the lumen of the ER and perinuclear space between outer and inner nuclear membranes (ONM and INM, respectively). We followed the different steps of nuclear elongation and nuclear division and correlated them with Ace2 localization. As previously reported, Ace2-GFP begins to enter the nucleus in midanaphase and localizes first to the entire nucleus (Colman-Lerner et al., 2001; Weiss et al., 2002). However, in cells with undivided dumbbell-shaped nuclei, the Ace2-GFP signal accumulated asymmetrically in the nuclear lobe located in the bud (Fig. 1 A). In time-lapse experiments, Ace2 asymmetry preceded fission of the bridge linking the two future nuclei by ∼8 min.

Fission of the inner membrane of the nucleus might precede disassembly of the bridge, but light microscopy does not have the resolution required to observe such an event. We therefore used nucleoplasmic spindle microtubules as a second marker to determine whether the nucleoplasm remains continuous during the establishment of Ace2 asymmetry. Using time-lapse microscopy, we monitored Ace2-GFP localization in cells coexpressing mCherry-Tub1 to visualize the relative timing of Ace2 asymmetry and spindle breakdown. In all cases (n = 51), Ace2 distribution became strongly asymmetric in cells with elongated, intact spindles (Fig. 1 B). Thus, Ace2 asymmetry is established before spindle breakdown and karyofission.

This observation suggests that some mechanism prevents Ace2 in the daughter part of the nucleus from diffusing back into the mother part. One possible mechanism for Ace2 retention in one half of the nucleus could be tethering of the protein to chromatin or other structurally constrained nucleoplasmic components. In this case, Ace2 would become immobilized in the daughter nucleus. To assess Ace2 mobility in the daughter nucleoplasm, we used fluorescence loss in photobleaching (FLIP) on cells with elongated, intact mitotic spindles visualized with mCherry-Tub1. We repeatedly bleached Ace2-GFP in one quarter of the daughter nucleus and monitored fluorescence levels in the opposite quarter (Fig. 1 C). The Ace2-GFP signal rapidly decayed over the entire nucleus. As a control, we repeated this procedure with cells expressing the histone Htb2-GFP (Fig. 1 D), which is stably incorporated into chromatin (Kornberg and Lorch, 1999). In contrast to Ace2-GFP, Htb2-GFP fluorescence decayed only slowly in the nonbleached part of the nucleus compared with the bleached area. Similarly, paraformaldehyde fixation of the cells stopped Ace2-GFP exchange between the bleached and unbleached parts of the nucleus (Fig. 1 E). This suggests that Ace2-GFP freely diffuses in the nucleoplasm. We conclude that the selective retention of Ace2-GFP in one half of the anaphase nucleus is not caused by immobilization of Ace2 in the bud nucleus.

We next investigated whether the anaphase nucleoplasm is compartmentalized. In this case, nucleoplasmic proteins should not freely exchange between mother and daughter. To test this possibility, we performed photobleaching experiments on tetracycline repressor (TetR)–GFP (Fig. 2 A). We performed these FLIP experiments at early and late stages of nuclear division, i.e., anaphase, as determined by nuclear morphology. The early stage of anaphase begins as soon as the nucleus enters the bud and contracts in the bud neck. This stage ends when a thin nuclear bridge forms between the two future rounded up nuclei. In late anaphase, the nucleus adopts a fully elongated, dumbbell-like shape, touching mother and daughter cell cortexes. Repetitive photobleaching of TetR-GFP fluorescence in a small area of the mother part of late anaphase nuclei led to rapid fluorescence loss in the mother, whereas fluorescence loss was much slower in the daughter nucleoplasm, and vice versa (Figs. 2 A and S1 A). Thus, the TetR-GFP exchange between the two halves of the nucleus is restricted. As reported previously, we detected no compartmentalization in early anaphase (Fig. 2 A; Shcheprova et al., 2008).

To extract quantitative information from these FLIP experiments, we determined the time required to lose 30% of the GFP fluorescence in mother and bud parts of the nucleus. The ratio of these two durations (bud over mother) expresses the different fluorescence decay rates in the two compartments upon bleaching the mother part of the nucleus. It is inversely proportional to the exchange rate between the two compartments. We termed this ratio “degree of compartmentalization” (°CP). In early anaphase, the °CP of TetR-GFP was around two (Fig. 2 E and Table S1). In late anaphase, it was 30-fold higher (Fig. 2 E).

Control FLIP experiments established that the vast majority of TetR-GFP exchange between mother and daughter occurs through the nuclear tube (Fig. S1, B–E). When we photobleached the cytoplasm of TetR-GFP–expressing cells, fluorescence barely decayed in the nucleus. Thus, TetR-GFP shuttling between nucleoplasm and cytoplasm had very little impact on the TetR-GFP exchange between mother and bud parts of the anaphase nucleus. Furthermore, we observed no exchange of TetR-GFP between nuclei in cells that had undergone karyofission but not cytokinesis. This was most obvious upon FLIP TetR-GFP in wild-type cells with separated nuclei (Fig. S1 C) and in cdc12-6 mutant cells incubated at 30°C (Fig. S1 E). At this temperature, cdc12-6 cells still divide their nucleus (Fig. S1 D) but fail to undergo cytokinesis (Dobbelaere and Barral, 2004).

TetR-GFP does not recognize any specific sequence in the yeast genome. Nevertheless, its ability to bind random DNA sequences with low affinity might affect its diffusion in the yeast nucleus and thereby contribute to its compartmentalization (Kleinschmidt et al., 1988). To test whether nonspecific DNA binding influences TetR diffusion, we measured the diffusion rates of TetR-GFP, TetR-Δhelix-turn-helix (HTH)-GFP, which lacks the DNA-binding motif, and a fusion of three GFPs with an NLS (NLS-3GFP) in vivo using fluorescence correlation spectroscopy (FCS; Orth et al., 2000). The nuclear diffusion coefficient of TetR-GFP was 1.9 ± 0.5 µm²/s (mean ± SD, n = 168; Fig. 2 F), whereas TetR-ΔHTH-GFP and NLS-3GFP diffused significantly faster (2.7 ± 0.9 µm²/s, n_TetRΔHTH = 204; 4.4 ± 2.5 µm²/s, n_NLS-3GFP = 179). Hence, nonspecific binding of TetR to DNA significantly affected its diffusion properties inside the nucleus. Therefore, transient binding of TetR to the separating chromatin masses during late anaphase might contribute to its compartmentalization.

For these reasons, we next investigated whether DNA binding is a prerequisite for compartmentalization. Using FLIP, no compartmentalization was observed for TetR-ΔHTH-GFP and NLS-3GFP during early anaphase (Fig. 2 E). However, in cells with dumbbell-shaped nuclei, the °CP increased 10-fold for TetR-ΔHTH and 15-fold for NLS-3GFP (Fig. 2, B–E; and Table S1). Thus, compartmentalization of nucleoplasmic proteins in late anaphase nuclei does not require DNA binding capability per se. The lower °CPs of TetR-ΔHTH-GFP and NLS-3GFP compared with TetR-GFP indicate that DNA binding only increases compartmentalization by a factor of two to three. We noticed that both NLS-3GFP and TetR-ΔHTH-GFP shuttled more rapidly between nucleus and cytoplasm than TetR-GFP (Fig. S1 F and not depicted). Therefore, DNA binding may enhance compartmentalization of TetR-GFP through nucleoplasmic retention of the protein.

Analysis of a soluble marker of the lumen between ONM and INM, GFP-HDEL, indicated that compartmentalization did not always increase as nuclear division progressed. First, no major compartmentalization effect was observed for GFP-HDEL during early anaphase (Fig. 2 E and Table S1). Second, the °CP of GFP-HDEL increased only threefold in late anaphase (Fig. 2, D and E; and Table S1). Thus, compartmentalization of the nucleoplasm is specific and does not affect the perinuclear space to the same extent.

Analysis of protein diffusion in the ONM and INM revealed yet another set of compartmentalization patterns. To assess the diffusion of nuclear pore complexes (NPCs) and ONM proteins, we performed FLIP experiments on the NPC protein Nup49-GFP and the ONM proteins Nsg1-GFP, Hmg1-GFP, and Hmg2-GFP (Basson et al., 1986; Wente et al., 1992; Flury et al., 2005). As reported previously, NPCs and ONM proteins were compartmentalized in early anaphase (Fig. 3, A and B; Shcheprova et al., 2008). During the early phase of nuclear division, Nsg1-GFP had a °CP of ∼7, whereas that of Nup49-GFP was much higher (Fig. 3 C and Table S1). The compartmentalization of the ONM markers increased six- to ninefold as the cells progressed through anaphase. Concerning Nup49-GFP, no exchange between the two nuclear halves was detectable in late anaphase. Using GFP-Src1, an INM protein homologous to LEM domain proteins in mammalian cells, and the artificial INM proteins LR1 and LR2, we confirmed that the exchange of INM proteins is rapid between mother and bud in early anaphase cells (Fig. 3, C and D; and Table S1; Rodríguez-Navarro et al., 2002; Grund et al., 2008; Meinema et al., 2011). However, as for Src1, a five- to sevenfold increase in compartmentalization was observed in late anaphase cells. Because LR1 and LR2 are fully artificial proteins, this compartmentalization is not caused by a specific interaction with, for example, scaffolding proteins. Thus, compartmentalization of the nuclear membrane increases in parallel to that of the nucleoplasm as anaphase progresses. These results show that, throughout nuclear division, compartmentalization increases not only in the nucleoplasm but also in both nuclear membranes. Compartmentalization of the ONM occurs first in early anaphase and increases at least by a factor of six as the nucleus adopts a dumbbell shape. Compartmentalization of the INM appears to occur only at this late stage.

We next wanted to determine where the boundary between the mother and daughter compartments is located within the internuclear bridge. Several options are possible: the boundary could be localized only to one specific part of the bridge, delocalized over the entire bridge, or each end of the bridge could form boundaries (Fig. 4 A). To distinguish between these possibilities, we performed FLIP experiments, bleaching each time a different small area in the bridge connecting the two future nuclei of late anaphase cells, and determined the °CP between the bud and mother parts of the nucleus, asking on what side of the compartments’ boundary we bleached the nucleus (Fig. 4 B). This became apparent when we correlated the °CP and its inverse (°CP⁻¹) with the position of the bleaching region in the tube (Fig. 4 C). The length of the entire nucleus was normalized to 100% to allow comparison between cells. The mean position of the bud neck was displaced slightly toward the bud half of the spindle, to position 58.1 ± 2.2% (mean ± SD, n = 20). The ends of the internuclear bridge were around positions 32.0 ± 3.4% in the mother and 70.9 ± 2.8% in the daughter. The ends of the tube were defined as the intersection points of the nuclear length axis with the extrapolated spherical outline of the respective daughter nuclei. We averaged the °CP values by bins of five cells with increasing distance of the photobleached area relative to the end of the nucleus in the mother cell. The resulting °CP value was plotted at the mean photobleaching position in the cells of the bin. The two curves described by the data points intersect at a °CP of one, marking the boundary between compartments. When bleaching on the mother side of the boundary, results in a °CP > 1, whereas bleaching on the daughter side results in a °CP between 1 and 0; the °CP⁻¹ should mirror this behavior. The curves for all three markers tested—GFP-Src1, Nsg1-GFP, and TetR-GFP—intersected at the spindle center rather than at the bud neck, suggesting that the boundary is in the bridge but not at the position of the bud neck. Furthermore, none of the curves showed any strong discontinuity in the tube or at its extremities, suggesting that, in all three cases, the entire bridge forms a gradual boundary. Therefore, the bridge might restrict exchange either through its geometry or through a diffusion barrier along the length of the bridge.

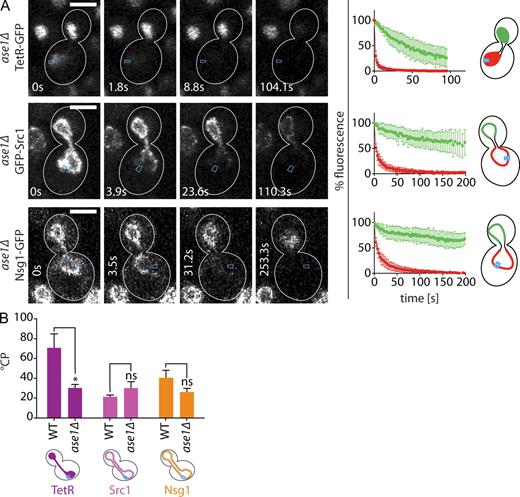
Because compartment boundaries were located on the spindle center in late anaphase, we next investigated whether the spindle midzone contributes to boundary formation. We deleted ASE1, which encodes a microtubule-binding protein localized at the spindle midzone. The ase1Δ mutation causes premature spindle breakdown and shortening of the dumbbell-shaped nucleus (Juang et al., 1997; Loïodice et al., 2005). To compare wild-type and ase1Δ cells, we restricted our FLIP experiments to dumbbell-shaped nuclei with a total length of 6–7 µm (Fig. 5). Nucleoplasmic compartmentalization decreased significantly in ase1Δ cells, as seen using TetR-GFP and NLS-3GFP as reporters (Figs. 5 B and S2 A and Table S1). However, the compartmentalization of the ONM and INM markers GFP-Src1 and Nsg1-GFP was unaffected compared with wild-type cells (Fig. 5). Interestingly, deleting BUD6 or SHS1, which has been shown to significantly decrease the °CP of Nsg1-GFP in early anaphase (Shcheprova et al., 2008), had no effect on Nsg1-GFP compartmentalization in dumbbell nuclei (Fig. S2, B and C). Thus, the ONM barrier is regulated differently in early compared with late anaphase. The effect of the ASE1 deletion on TetR-GFP exchange indicates that Ase1 contributes to nucleoplasmic compartmentalization. In contrast, it does not affect the compartmentalization of INM and ONM, indicating that the nucleoplasm and the membranes are compartmentalized through different mechanisms.

Deleting ASE1 shortens the overall length of the anaphase nucleus but also reduces bridge length (Fig. S2 E). We next asked how important this change in nuclear geometry is for compartmentalization. Therefore, we plotted the °CP of individual cells against their bridge length to test whether these parameters correlate with each other (Fig. 6 A). The compartmentalization of TetR-GFP correlated well with bridge length, whereas that of GFP-Src1 and Nsg1-GFP did less. Consequently, in wild-type and ase1Δ strains, the °CP of TetR-GFP was on average higher in nuclei with longer bridges than in those with shorter bridges. Thus, the effect of the ase1Δ mutation on bridge length at the end of anaphase probably contributed to the effect of this mutation on compartmentalization. However, ase1Δ mutant cells showed an additional loss of nucleoplasmic compartmentalization that was independent of bridge length, as demonstrated by the observation that at a given length, the ase1Δ mutant showed a lower °CP for TetR-GFP than the respective wild type. This could be caused either directly by the midzone plugging the tube of wild-type cells or indirectly by a change of bridge diameter in ase1Δ cells.

Thus, we next investigated which of plugging the bridge with the spindle midzone, bridge dimensions, and correct positioning of the dumbbell-shaped nucleus relative to the bud neck is most important for nucleoplasmic compartmentalization. Therefore, we first measured the length and width of the bridge in nuclei of several knockout strains (Figs. 6 B and S2, C–E). For this, the bridge width was assessed through the total fluorescence intensity of the Nsg1-GFP marker per length unit of the bridge (Fig. S2 E). Indeed, the intensity of GFP fluorescence per bridge length is expected to correlate linearly with the diameter of the bridge because the density of Nsg1-GFP fluorescence in the ONM was not significantly different in all strains tested (Fig. S2 C). Several knockout strains showed reduced bridge length and increased bridge diameter, including ase1Δ, the kinesin cin8Δ, the dynein heavy chain dyn1Δ, and a strain lacking both the spindle orientation checkpoint component BUB2 and the dynactin component ARP1 (Fig. S2, D and E; Hoyt et al., 1991, 1992; Roof et al., 1992; Saunders and Hoyt, 1992; Eshel et al., 1993; Li et al., 1993; Muhua et al., 1994). Whereas nuclei measured in ase1Δ or cin8Δ cells crossed the bud neck, nuclei measured in dyn1Δ and bub2Δarp1Δ divided in the mother cell, i.e., displaced relative to the bud neck. Nuclei of cnm67Δ cells dividing away from the bud neck also showed slightly increased bridge diameters but no changes in bridge length. Cnm67 is a spindle pole body component (Brachat et al., 1998). Deleting the cohibin complex components LRS4 and CSM1 had the same consequences for nuclear architecture as the CNM67 deletion but did not displace the dividing nuclei from the bud neck (Smith et al., 1999; Huang and Moazed, 2003; Rabitsch et al., 2003; Mekhail et al., 2008). The slk19Δ mutant cells had nuclei with longer and slightly wider, but correctly placed, bridges. Slk19 is a signaling protein involved in spindle dynamics and exit from mitosis (Zeng et al., 1999; Stegmeier et al., 2002; Neurohr et al., 2011). To assess the contribution of the individual geometries to nucleoplasmic compartmentalization, we correlated the °CP of TetR-GFP in the knockout strains with the bridge length normalized to its cross section. Remarkably, across all strains and situations considered, °CP and normalized bridge length remained proportional to each other (Fig. 6 C). Mutants that displaced their anaphase nucleus from the bud neck, as well as those placing it correctly, follow the same linear correlation between bridge geometry and compartmentalization of the nucleoplasm.

To investigate the role of the spindle as an obstacle restricting exchange between mother and daughter nucleoplasm, we compared the spindle in dumbbell-shaped nuclei of ase1Δ and cin8Δ cells using Nsg1-GFP to outline the nuclear periphery and mCherry-Tub1 to visualize the spindle. Both mutants had low °CPs and similar geometry defects, although in the ase1Δ mutants cells, 60% of the dumbbell nuclei showed no continuous mCherry-Tub1 signal in the bridge, whereas virtually all cin8Δ cells did (Fig. 6, D and E). We conclude that the absence of microtubule bundles in the bridge is not the main cause of the compartmentalization defect observed in ase1Δ.

Overall, the correlation between the geometry of the dividing nucleus and the °CP of TetR-GFP strongly suggests that nuclear morphology is the main determinant for nucleoplasmic compartmentalization. The spindle midzone itself and the bud neck have much less impact on this process, if any.

To theoretically dissect the impact of geometry and potential diffusion barriers on nuclear compartmentalization, we next used off-lattice spatial stochastic simulations in idealized cells during early and late stages of nuclear division. In off-lattice simulations, the simulation domain is usually discretized to efficiently localize particles, yet each particle can diffuse and react while preserving explicit coordinates at all time points (Burrage et al., 2011; Marquez-Lago et al., 2012). Such particle methods yield the highest available accuracy of microscopic cellular dynamics, which was set to 20 nm in our case. Therefore, they provide the ideal basis to test whether diffusion barriers need to be introduced to reproduce in silico the compartmentalization observed in our FLIP experiments in vivo.

After defining simulation geometries for the nucleus during early and late stages of division, separate simulations were run using Smoldyn 2.22 for each molecular species, in each distinctive domain of the nuclear space, and within different timescales (see Materials and methods; Fig. S3; Andrews et al., 2010). First, we determined four necessary parameters to carry out simulations of our FLIP experiments presented in Figs. 2 and 3: the number of diffusing particles, the rate of photobleaching in the irradiated area, the diffusion rates of the different molecules, and the strength of any potential diffusion barrier. The determination of the first three parameters can be found in the Materials and methods section. Here, we describe the outcome of the simulations concerning the contribution of potential diffusion barriers in the process of matching experimental and simulated data.

To reproduce the in vivo FLIP experiments on Nsg1, Nup49, Src1, and TetR, we performed parameter sweep simulations assuming various diffusion coefficient values and barriers of different strengths. We defined barriers as a constraint on the given particle allowing it to pass from one to the opposite nuclear lobe at a set probability (p). These barriers were formed by a plane covering the area defined by the bud neck in early anaphase or the middle of the cylinder connecting the future mother and bud nucleus in late anaphase. The value p = 1 indicates that no barrier is present. Values <1 indicate the presence of a barrier acting beyond morphology, whereas values >1 indicate directed transport from one compartment to the other. Because there was no experimental evidence for the latter, we did not include directed transport in the current model. Moreover, we assumed that the passage probability is symmetric, i.e., not dependent on the side from which the particle originated. Subsequently, we determined the distances between the modeled and experimental decay curves.

To explain the behavior of TetR in the nucleoplasm during early and late anaphase, no diffusion barrier is needed, as experimental data and simulation already matched at p = 1 (Figs. 7, A and D; and S4, A and B). Therefore, changes in geometry account for most, if not all, changes in nucleoplasmic compartmentalization as cells progress through anaphase. Simulations performed on TetR-GFP in nuclei with changed bridge morphologies further support this idea (Fig. S4 C): dilating the bridge 3.4-fold decreased the compartmentalization of TetR-GFP approximately eightfold. Shortening the tube to a third of its original length reduced compartmentalization ∼2.5-fold. The combination of both conditions abolished compartmentalization. These results are consistent with the dimensions of the tube having a strong impact on nucleoplasmic compartmentalization, as suggested by the experimental results (Fig. 6 C).

A strikingly different situation was observed for Nsg1, Nup49, and Src1: all simulations that did not assume the existence of a lateral diffusion barrier in the plane of the membrane failed to accurately reproduce the experimental data of fluorescence loss (Fig. 7, B, C, E, and F). In the case of Nsg1 particles, the probability of crossing the boundary had to be reduced to 12% of unrestrained conditions in early anaphase and 5% in late anaphase to replicate the behavior seen in vivo (Fig. 7, B and E). For Nup49 and Src1, these probabilities were 2.5 and 25%, respectively, independently of whether the nuclei were in early or late stages of nuclear division (Figs. 7, C and F; and S4, A and B). Details on how deviations from experimental data arose in mother and bud compartments are presented in Fig. S5.

The simulations show that the nucleoplasm is compartmentalized because of its geometry. In contrast, diffusion barriers play a major role in subdividing the nuclear membranes into a mother and a daughter compartment throughout nuclear division.

Our observations show that the morphological events associated with closed mitosis in budding yeast passively promote compartmentalization of the nucleoplasm during late stages of nuclear division. However, this compartmentalization might be needed to promote selected processes, such as Ace2 segregation. Therefore, we tested whether mutations altering nucleoplasmic compartmentalization affect the behavior and distribution of Ace2.

Using FRAP and FLIP, we characterized the dynamics of Ace2. First, we used FRAP to study the compartmentalization of the Ace2-F127V variant, which is trapped in mother and daughter nuclei (Racki et al., 2000; Mazanka et al., 2008). Consistent with our data on nucleoplasmic compartmentalization, the signal in the mother nucleus recovered slowly upon photobleaching before spindle breakdown as visualized by mCherry-Tub1 (Fig. 8 A). In contrast, recovery was rapid in ase1Δ mutant cells coinciding with the loss of fluorescence in the daughter half of the nucleus. Similarly, when Ace2-GFP was bleached continuously in the mother half of the nucleus, fluorescence was lost slowly in the daughter half, whereas fluorescence loss was faster in similarly treated ase1Δ mutant cells (Fig. 8 B). We conclude that, similar to our observations of TetR-GFP, the dimensions of the internuclear bridge limit the exchange of Ace2 between the two halves of dumbbell-shaped nuclei. Thus, compartmentalization contributes to the retention of Ace2 in the daughter nucleus before karyofission.

To test whether compartmentalization contributes to Ace2 asymmetry, we investigated whether compartmentalization mutants displayed altered Ace2 segregation upon cell division. Fluorescence measurements in cells after karyofission as visualized by dsRed-HDEL indicated that Ace2-GFP was distributed more symmetrically in ase1Δ and cin8Δ cells (Fig. 8, C and D). Deleting SLK19, which increases nucleoplasmic compartmentalization, slightly increased Ace2 asymmetry. Furthermore, Ace2-S122A distributed more symmetrically in ase1Δ cells (Fig. 8 E). Ace2-S122A is mutated in one of its two Cbk1 sites close to the nuclear export signal and is partially defective in establishing Ace2 asymmetry (Mazanka et al., 2008). Nevertheless, the symmetry is not as complete as in cells expressing Ace2-AA-GFP lacking both Cbk1 phosphorylation sites (Mazanka et al., 2008). Interestingly, the effect of the S122A mutation on Ace2 segregation was partially suppressed in slk19Δ. Collectively, these data indicate that compartmentalization contributes to the maintenance of Ace2 asymmetry, whereas the RAM pathway establishes Ace2 asymmetry and prevents full Ace2 symmetry in ase1Δ and cin8Δ cells. We conclude that nucleoplasmic compartmentalization and the RAM network contribute synergistically to the asymmetric segregation of Ace2.

In this study, we show that during late anaphase, the nucleus of budding yeast is extensively compartmentalized. Unlike in early stages, during which exchange between mother and bud is not limited in nucleoplasmic compartments, all nuclear spaces become strongly compartmentalized in late mitosis, when the nucleus adopts a dumbbell-like shape. This compartmentalization has clear functional consequences for the cell. By limiting the exchange of the transcription factor Ace2 between mother and bud parts of the nucleus, compartmentalization of the nucleoplasm supports the establishment of Ace2 asymmetry and promotes its inheritance by the daughter cell. Thus, when Ace2 asymmetry is important, nucleoplasmic compartmentalization is likely to confer a selectable advantage to the cell. In other words, mechanisms that ensure compartmentalization of the nucleoplasm could have emerged at least partially in coevolution with Ace2 asymmetry.

Using a combination of experimental and simulated FLIP data, together with mutants affecting spindle organization and nuclear morphology, we could distinguish between the contribution of geometry and the permeability of potential diffusion barriers to nuclear compartmentalization. These experiments establish the following three points.

First, compartmentalization of the nucleoplasm is well explained by the geometry of the nucleus alone. Accordingly, parameters such as the length and width of the bridge connecting the two future daughter nuclei determine the °CP.

Second, compartmentalization of nucleoplasmic proteins is increased for those that are able to bind DNA even with low affinity, such as TetR. This twofold increase in compartmentalization is likely to be mediated by three convergent processes: the separation of the segregating chromosomes into two disjoint masses, the reduction of the diffusion speed of the protein, and its increased retention in the nucleus, which limits exchange via the cytoplasm.

Third, in contrast to what is observed in the nucleoplasm, the compartmentalization of the nuclear membranes cannot be explained by their geometry alone. Already in early anaphase, the dynamics of markers in both the INM and ONM are best explained by the presence of a barrier, which limits lateral diffusion around the spindle midzone, in addition to geometry. Accordingly, in both membranes, the length of the internuclear bridge only modestly affected compartmentalization. Most remarkably, the width of the bridge, which had a strong impact on the compartmentalization of the nucleoplasm, made no clear contribution to the compartmentalization of the INM and ONM.

In a previous study, we found that specialized membrane structures are present in the cortical ER at the bud neck (Luedeke et al., 2005). These structures contribute to the formation of lateral diffusion barriers at the mother–bud junction. Further studies will be needed to investigate whether membrane compartmentalization in the nuclear envelope follows the same rules. If this is the case, it will be interesting to investigate whether compartmentalizing structures are primarily dedicated to other functions, compartmentalization being a secondary consequence, or whether they are primarily dedicated to barrier formation. For example, functionally specializing the nuclear membranes in the connecting bridge of late anaphase nuclei might be more relevant for spindle stability, chromosome segregation, or karyofission rather than compartmentalization. However, the observation that the passive compartmentalization of the nucleoplasm plays an important role in promoting the asymmetry of cell division suggests that nuclear compartmentalization in its own right is an important function of the interconnecting bridge. Also, the observation that the bud6Δ mutation, which does not appear to affect nuclear morphology, enhanced the exchange between the mother and bud part of the ONM in early, but not in late, anaphase suggests that several independent mechanisms contribute to ONM compartmentalization. Thus, compartmentalization of this membrane appears to be a tightly controlled process.

Altogether our data support the notion that compartmentalization of the nucleus is an important aspect of the process of closed mitosis, most probably because it serves as a support for the asymmetric segregation of nuclear components, such as daughter-specific transcription factors and nonchromosomal DNA (Shcheprova et al., 2008). A corollary of this conclusion is that the dumbbell shape of the nucleus is not circumstantial but the result of a complex evolution leading to the adaptation of the process of nuclear division to biologically relevant constraints, beyond karyofission.

Accordingly, it is interesting to note that the morphological events associated with nuclear division are highly variable in fungi. For example, the dividing nucleus of the fission yeast Schizosaccharomyces japonicus does not develop the dumbbell morphology typical of S. cerevisiae and Schizosaccharomyces pombe and undergoes semi-open mitosis instead (Aoki et al., 2011; Yam et al., 2011). Hence, it is very likely that this organism, which apparently divides highly symmetrically, shows no compartmentalization of the nucleoplasm. It will be interesting to determine whether it does establish barriers in the nuclear envelope. Investigating the biological consequences of the different forms of nuclear division will shed light on the origins and roles of compartmentalization mechanisms.

From that perspective, gaining a molecular understanding of the mechanisms controlling the morphology and compartmentalization of the dividing yeast nucleus is likely to provide also important information about the process of mitosis in a general sense. Little is known about how the nuclear envelope is shaped and how this process is controlled as the spindle elongates and the nucleus acquires its dumbbell morphology. Understanding the contribution of Ase1, Cin8, and Slk19 in this process will provide insights about how microtubules of the spindle midzone interact with the nuclear membrane in fungi as well as how the same structure interacts with the plasma membrane during the cytokinesis of animal cells. However, clearly Ase1 and the spindle midzone are not the only factors involved in shaping the anaphase nucleus. Further studies will be required to investigate the role of the other components of the nucleus, such as chromatin, and to identify the machineries involved in membrane dynamics, curvature, and cleavage during the highly sophisticated process of nuclear division.

All yeast strains were constructed according to standard genetic techniques (Guthrie, 1991) and are isogenic to S288C. The yeast strains used in this study and their references are listed in Table S2. All experiments were performed with three individual clones, of which one is listed in Table S2. All cultures or plates were grown at 30°C unless indicated otherwise.

For all FLIP experiments in Figs. 2, 3, 4, 5, 6, S1, and S2, cells were grown at 30°C on YPD (yeast, peptone, and dextrose) plates, resuspended in synthetic complete medium, and immobilized on a 2% agar pad containing synthetic complete medium. The cells were imaged on a confocal microscope (LSM 510; Carl Zeiss) with a Plan Apochromat 63×/1.4 NA oil immersion objective, typically using 2% of the laser intensity of an argon laser (488-nm line) at 45% output. The ZEN 2010 software (Carl Zeiss) was used to control the microscope. GFP emission was detected with a 505-nm long pass filter. Photobleaching was applied on the selected area as indicated in the figures. Bleaching pulses were iterated 80 times at 60% of the laser intensity at 45% output. All photobleaching experiments were performed at 30°C.

Photobleaching experiments on Ace2-GFP and HTB2-GFP (Figs. 1, C–E; and 8, A and B) were performed on cells grown in liquid culture in the exponential phase for 5 h at 30°C. Cells were harvested by centrifugation, resuspended in synthetic complete medium, and immobilized on a 2% agar pad containing synthetic complete medium. FLIP and FRAP experiments on Ace2-GFP were performed using a confocal microscope (LSM 710; Carl Zeiss) using a Plan Apochromat 63×/1.4 NA oil immersion objective. GFP was excited with the 488-nm line of an argon laser, whereas mCherry was excited with a 561-nm solid-state laser. The signals were detected with a band pass (bp) 505–540-nm (GFP) and a bp 620–660-nm filter (mCherry).

Quantification was performed using ImageJ 1.42q (National Institutes of Health). The mean fluorescence signal was quantified in the entire daughter, the entire mother part of the nucleus, and in the nuclei of five neighboring cells. After background subtraction, the fluorescence signals of the mother and daughter part were normalized to the mean of the five control nuclei and set to 100% at beginning of the experiment. All experiments were pooled and transferred to Prism 5.0b (GraphPad Software), in which they were fitted a one-phase decay curve constraining the starting point to 100%. The °CP was defined as the ratio of the times needed to lose 30% of the fluorescence signal in the bud over the mother. All images shown in the figures were processed using ImageJ 1.42q and Photoshop CS4 extended version 11.0.2 (Adobe).

All experiments using wide-field microscopy (Figs. 1, A and B; 6, D and E; 8, C–E; S1 D; S2, C–E, G, and H; and S3) were performed on a microscope (DeltaVision; Applied Precision) with a 100×/1.40 NA U Plan S Apochromat oil immersion objective (Olympus), a 250-W Xenon lamp, and a charge-coupled device camera (CoolSNAP HQ²; Photometrics) using softWoRx software (Applied Precision). Noise was reduced in all wide-field images acquired using 3D iterative constrained deconvolution by the software softWoRx. Image analysis was performed with ImageJ 1.42q.

Time-lapse microscopy on Ace2-GFP (Fig. 1, A and B) and on nuclear division using Nsg1-GFP (Fig. S1 D) was performed with a z spacing of 400 nm and binning of 2. The pause between the time points was 2 min for Ace2-GFP and 5 min for Nsg1-GFP. Although GFP fluorescence was exited with wavelengths from 461 to 489 nm and detected between 525 and 550 nm, mCherry or dsRed were excited at 563–588 nm and detected between 632 and 660 nm.

The z stacks to describe nuclear shape using Nsg1-GFP (Figs. 6, D and E; S2, C–E, G, and H; and S3), Ace2-GFP distribution (Fig. 8, C–E), and spindles in late stages of nuclear division (Fig. 6, D and E) were recorded with a spacing of 200 nm between the individual planes and without binning. To describe thickness of the tube using Nsg1-GFP fluorescence, the total fluorescence per micrometer of bridge length was measured on summed intensity projections of the full stacks measuring the integrated fluorescence over the whole area of the tube; the background subtracted was measured next to the tube inside the cell. Ace2-GFP and dsRed-HDEL were imaged with different filter sets than described in the previous paragraph (GFP: excitation of 461–489 nm and emission of 523–536 nm; dsRed: excitation of 529–556 nm and emission of 594–645 nm). The distribution of Ace2 was determined based on the integrated density of GFP signal measured in both nuclei outlined by dsRed-HDEL. After subtracting the background inside the cell, a ratio of mother signal over bud signal was calculated.

FCS allows the analysis of fluorescence intensity fluctuations caused by fluorophore diffusion through a small (approximately femtoliter) detection volume (Elson, 1974; Rigler and Elson, 2001; Bacia and Schwille, 2003; Petrov and Schwille, 2008). In this study, FCS measurements were performed on a microscope (LSM 710 ConfoCor3; Carl Zeiss) with a 40× 1.2 NA UV-visible infrared C Apochromat water immersion objective using the ZEN 2010 software. Cells were grown at 25°C and immobilized between a glass slide and a coverslip. The experiments were performed at 25°C. FCS measurements were performed in the yeast nucleus for 30 s, with excitation by a 488-nm laser with <0.5 µW. The emission signal was detected with a bp 505–540-nm filter. Curves were fitted to a diffusion model describing one diffusing species, including photophysics of the fluorescent protein, with an additional offset accounting for the effects of photobleaching of the fluorophores. The confocal volume aspect ratio parameter was set to seven.

To determine the dimensions of the early stage simulation domain, we performed measurements on dividing nuclei expressing Nsg1-GFP imaged on a microscope (DeltaVision) with a 100× oil immersion objective using the softWoRx software. In total, 21 nuclei were analyzed denoting: (a) total length of the mother–bud nuclear complex, (b) length of mother end to bud neck, (c) diameter of mother, (d) diameter of ingression at bud neck, and (e) diameter of bud (Fig. S3 A), assuming the intermembrane space to be 60 nm wide. The geometry was then built based on the mean dimensions of all 21 cells measured (Fig. S3 C). From these measurements, idealized truncated ellipsoids joined at their edges with distinct radii were determined, in which the size of the angle determining the truncation was calculated.

Similarly, for the late stage, we obtained a mean spherical radius and mean bridge length connecting to the mother and bud nuclei from 34 cells. The corresponding simulation geometry was idealized as two truncated spheres joined by a cylinder. The diameter of the bridge on the level of the ONM and the thickness of the perinuclear space (early and late) were extracted from transmission EM pictures recorded by Winey et al. (1995; Fig. S3 C).

An ellipsoid can be parametrically described as: x = r_x cos(u) sin(v) + x₀, y = r_y sin(u) sin(v) + y₀, and z = r_x cos(v) + z₀, in which u ε [0,2π), v ε [0,π), x₀, y₀, and z₀ are the coordinates of its center, and r_x, r_y, and r_z are the axis lengths in the x, y, and z directions. In a truncated ellipsoid, the angle v will naturally have a different lower or upper value, and in a sphere, the axis lengths are r_x = r_y = r_z. Accordingly, the model geometries for the simulation of early and late stages of nuclear division were set as described in Fig. S3 (C and D), where it should be noted, the radial distances in the z axis are identical to those in the y axis. Once the compartments were defined parametrically, Delaunay triangulations were performed, yielding the final discretization of the simulation domains.

To determine the number of Nsg1-GFP and GFP-Src1 molecules, we relied on the quantification data from the Yeast GFP Fusion Localization Database (Ghaemmaghami et al., 2003; Huh et al., 2003) because we needed information about the relative amounts rather than the exact numbers of molecules per cell. Both proteins were present in ∼2,000 copies per cell (2,100 for Src1 and 1,900 for Nsg1). Based on the total amount of TetR-GFP fluorescence, we estimated ∼5,000 copies of TetR-GFP per cell. In the case of Nup49-GFP, simulations were run with 150 particles of 16 molecules each per nucleus, which reflects the number of NPCs with the according number of molecules per complex (Winey et al., 1997; Alber et al., 2007).

A bleaching area, in the shape of a cigar, was set to be centered at (−1.5595, 0.731, 0) in early stage mother cells, and at (−1.01, 0.9982, 0) in late stage mother cells. For all simulations, the radial dimensions of such bleaching region in each dimension were b_x = b_y = 0.14 µm and b_z = 0.23 µm.

It is worth noting that experimental variability may result from samples with different bleaching intensities, while assuming uniform diffusion coefficients. The latter can, in principle, account for parts of the variation bounds in experimental measurements, the major part stemming from differences in single cell sizes.

To make accurate fluorescence loss calculations, one needs to confirm a diffusion constant or bleaching rate experimentally. Because we had already determined the diffusion rate of TetR-GFP by FCS (Fig. 2 F) and because TetR-GFP is not compartmentalized in early anaphase, the bleaching rate could be determined from simulations of the FLIP experiments performed with TetR-GFP, presented in Fig. 2 A. The bleaching rate was defined as a degradation rate for molecules entering the bleaching region. During these simulations, 5,000 TetR particles diffusing at a rate of 1.9 µm²/s were uniformly distributed within the nucleoplasm. Fluorescence decay was estimated as a decay rate for particles inside the bleaching region, allowing an individual particle to potentially escape. From this, we estimated an optimal degradation rate of k_deg = 110/s. Because this number refers to the speed at which particles can be bleached to fit the experimental data, it does not depend on the compartment where the particles diffuse, i.e., the nucleoplasm, INM, or ONM. Thus, it was used uniformly in fluorescence loss simulations of TetR, Nsg1, Nup49, and Src1. Remarkably, preliminary simulations with TetR-GFP also revealed the impossibility to match experimental FLIP data by using the diffusion rates classically assumed for a protein of this size, stressing out the role of nonspecific DNA binding in TetR dynamics.

To determine how many particles should be placed in each of the parts comprising a single simulation compartment, we calculated the nucleoplasm volume (for TetR) and the surface area of the INM (for Src1 and Nup49) and ONM (for Nsg1) in both early and late stages of nuclear division. The number of molecules in each section of a compartment was thus scaled according to the volume or the surface area, depending on whether the molecules diffuse in 3D or 2D.

The volume of an ellipsoid is given by 4/3π r_x r_y r_z, and we made a rough approximation of the missing volume from each truncated ellipsoid by calculating the volume of a similar spherical cap. The latter can be calculated as πh/6 (3δ + h²), in which the thickness of the cap is denoted by h, and the radius of the base of the cap is δ. The surface area of a prolate ellipsoid with a circular equator, as is our case, can be calculated as 2π (r_x² + r_z² (α/tanα)), in which α = arcos(r_x/r_y), whereas the surface area of a spherical cap is π(δ² + h²). The volumes and surface areas of spheres and cylinders are straightforward.

In the last step, we estimated diffusion rates of membrane-bound particles by minimizing the error of the first moment, i.e., the mean of the stochastic simulations, over their ensembles. We performed these simulations in equal numbers of the samples from the FLIP experiments to which they were compared. This approach yielded the following parameters in the ONM and INM simulations: The 2,000 Nsg1 particles equally distributed within mother and bud ONM compartments diffused at a rate of 0.3 µm²/s, whereas the 150 Nup49-containing particles uniformly distributed within the ONM/INM diffused at a rate of 0.2 µm²/s. The 2,000 particles of Src1 equally distributed within the INM mother and bud compartments diffused at the same rate as the Nsg1 particles (0.3 µm²/s). Noticeably, in the cases of Nup49 and Src1, optimal diffusion rates were not found to match either the early or late stages of nuclear division. For the latter, slower diffusion coefficients were estimated (0.125 and 0.2 µm²/s, respectively). The curvature of the fluorescence loss profiles could, in principle, be caused by time-varying diffusion rates. A thorough analysis could be performed to determine whether fractional or Brownian diffusion is to be expected (Marquez-Lago et al., 2012).

Fig. S1 shows that TetR-GFP does not exchange between the cytoplasm and nucleoplasm. Fig. S2 describes the impact of mutants described in Fig. 6 on nuclear geometry and nuclear compartmentalization in more detail. Fig. S3 shows the nuclear geometries constructed for the simulations. Fig. S4 compares the simulation results to the actual FLIP data. Fig. S5 differentiates the deviations between the simulations and the experimental mean arising in the mother and bud compartment. Table S1 contains °CPs with errors and numbers of cells imaged. Table S2 indicates the yeast strains used in this study.

T.T. Marquez-Lago would like to thank André Leier for suggestions on the modeling and computational implementation. Furthermore, the authors thank Liesbeth Veenhoff, Ed Hurt, and Stefan Westermann for sharing constructs and strains, the Light Microscopy Center at the Swiss Federal Institute of Technology Zürich, the Molecular Life Sciences PhD program, and all members of the Barral laboratory and Jonas Ries for helpful discussions.

E.L. Weiss was supported by the National Institutes of Health grant GM084223. B. Boettcher was supported by the BarrAge grant from the European Research Council to Y. Barral.