The force response of cardiac muscle undergoing a quick stretch is conventionally interpreted to represent stretching of attached myosin crossbridges (phase 1) and detachment of these stretched crossbridges at an exponential rate (phase 2), followed by crossbridges reattaching in increased numbers due to an enhanced activation of the thin filament (phases 3 and 4). We propose that, at least in mammalian cardiac muscle, phase 2 instead represents an enhanced detachment rate of myosin crossbridges due to stretch, phase 3 represents the reattachment of those same crossbridges, and phase 4 is a passive-like viscoelastic response with power-law relaxation. To test this idea, we developed a two-state model of crossbridge attachment and detachment. Unitary force was assigned when a crossbridge was attached, and an elastic force was generated when an attached crossbridge was displaced. Attachment rate, f(x), was spatially distributed with a total magnitude f0. Detachment rate was modeled as g(x) = g0+ g1x, where g0 is a constant and g1 indicates sensitivity to displacement. The analytical solution suggested that the exponential decay rate of phase 2 represents (f0 + g0) and the exponential rise rate of phase 3 represents g0. The depth of the nadir between phases 2 and 3 is proportional to g1. We prepared skinned mouse myocardium and applied a 1% stretch under varying concentrations of inorganic phosphate (Pi). The resulting force responses fitted the analytical solution well. The interpretations of phases 2 and 3 were consistent with lower f0 and higher g0 with increasing Pi. This novel scheme of interpreting the force response to a quick stretch does not require enhanced thin-filament activation and suggests that the myosin detachment rate is sensitive to stretch. Furthermore, the enhanced detachment rate is likely not due to the typical detachment mechanism following MgATP binding, but rather before MgADP release, and may involve reversal of the myosin power stroke.
Introduction
Muscle performance is often gauged in terms of contractile force and power. The capacity to relax and relengthen is also critical to the function of many muscle types. Cardiac muscle, for example, must relengthen during the diastolic phase of the cardiac cycle to ensure adequate ventricular chamber filling. A slowed or partially completed filling of the left ventricle (LV) is a pathophysiologic mechanism underlying ≥50% of all cases of heart failure and is a growing societal health concern (Dunlay et al., 2017). One factor affecting diastolic function is the force-producing myosin enzyme, which will inhibit relengthening if still attached to actin as diastole progresses.
The most influential determinant of myosin detachment from actin is the rate-limiting MgADP release step. A slower MgADP release rate, as occurs in the cardiac β-myosin isoform compared with α-myosin, for example, prolongs the lifetime of the force-producing myosin crossbridge (Tyska and Warshaw, 2002). The longer-lived crossbridge, in turn, slows the decay of muscle contractile force during relaxation and thereby would be expected to inhibit myocardial lengthening in diastole (Kass et al., 2004). The MgADP release rate is also slowed when a resistive load, as occurs with muscle lengthening, is applied to the myosin crossbridge (Veigel et al., 2005; Kad et al., 2007; Liu et al., 2018). These two factors, the predominance of β-myosin isoform in the human LV and the strain-dependent slowing of MgADP release during myocardial lengthening, work against myocardial relengthening and diastolic function.
Conversely, mechanisms within the myofilaments that enhance the crossbridge detachment rate in response to stretch would benefit diastolic function by reducing the mechanical energy required to lengthen the myocardium. One possibility is an additional, faster crossbridge detachment pathway before MgADP release, perhaps coincident with rebinding of inorganic phosphate (Pi). A Pi-dependent crossbridge detachment before MgADP release has been shown to be facilitated by a resistive load as occurs with muscle lengthening (Dantzig et al., 1992; Smith and Geeves, 1995) and, therefore, could play a role in decreasing resistance during myocardial lengthening. Such a mitigation of cardiac force during lengthening has been reported in intact myocardium undergoing stretch in late systole (Chung et al., 2017).
The idea that myosin crossbridges are more likely to detach during stretch suggests an alternative interpretation of the experimentally observed force response to a quick stretch. The current prevailing interpretation includes an enhancement of thin filament activation with stretch, frequently referred to as stretch activation (Campbell, 1997; Campbell and Chandra, 2006). We would argue that, because cardiac muscle retains the familiar force response to a quick stretch even after removal of thin-filament regulatory proteins (Kawai and Ishiwata, 2006), the typical features of the force response to stretch in cardiac muscle do not rely on effects of thin-filament regulatory proteins. Our proposed enhancement of detachment rate with stretch does not focus on any strain effects on MgADP release rate, but rather on some other strain-dependent pathway possibly involving Pi rebinding (Smith and Geeves, 1995). In this paper, we present the basis of a hypothesis that a strain-dependent enhancement of the myosin crossbridge detachment rate underlies the salient features of the force response to stretch.
Materials and methods
Solutions
Chemicals and reagents were obtained from Sigma-Aldrich unless otherwise noted. Krebs solution contained (in mmol/liter) 127 NaCl, 2 KCl, 1.3 KH2PO4, 2.5 CaCl2, 0.6 MgSO4, 25 NaHCO3, and 10 glucose, pH 7.4; nonactivating solution: calcium concentration (pCa) 8.0, 5 EGTA, 5 MgATP, 1 Mg2+, 0–8 Pi, 35 phosphocreatine, and 300 U/ml creatine kinase, ionic strength 200, pH 7.0; activating solution: same as nonactivating, with pCa 4.0; rigor solution: same as relaxing, with pCa 4.8 and 0 MgATP; skinning solution: same as relaxing, without creatine kinase and with 1% Triton X-100 wt/vol, 10 µl/ml E-64, 1.25 µl/ml PMSF, 1 tablet/10 ml PhosStop phosphatase inhibitor cocktail, and 50% glycerol wt/vol; storage solution: same as skinning, without Triton X-100. Where indicated, the myosin crossbridge inhibitor 2,3-butanedione 2-monoxime (BDM) was added at 40 mM.
Mouse myocardium
All procedures were reviewed and approved by the Institutional Animal Care and Use Committee of the University of Vermont College of Medicine and complied with Guide for the Use and Care of Laboratory Animals published by the National Institutes of Health. Animals were fully anesthetized with isoflurane and hearts were removed. Papillary muscles from the LV were isolated, removed, and placed in preoxygenated (95% O2, 5% CO2) Krebs-Ringer solution at room temperature and demembranated overnight at 4°C in skinning solution. Skinned myocardial strips were prepared and studied as previously described (Donaldson et al., 2012; Zile et al., 2015). Strips were mounted between a piezoelectric motor (P841.60, Physik Instrumente) and a strain gauge (AE801, Kronex), lowered into a 30-µl droplet of relaxing solution maintained at 17°C, and stretched to 2.2 µm sarcomere length (IonOptix). Strips were subjected to activating and rigor solutions to induce distinct experimental conditions. Force responses were recorded after step-length changes of 0.25, 0.5, or 1.0% resting muscle length (ML). In some cases, constant velocities were imposed at 1, 0.5, 0.2, 0.1, and 0.05 ML/s, which corresponded to 1% ML change over 10, 20, 50, and 100 ms.
Human myocardium
All patients signed informed consent forms approved by the University of Vermont Institutional Review Board. LV epicardial biopsies were obtained during coronary bypass graft procedures as described previously (Donaldson et al., 2012; Zile et al., 2015). Skinned strips were prepared and examined as described for mouse myocardium above but at 37°C.
Computer simulations
Computer simulations were performed using IDL v8.4 (Exelis Visual Information Solutions). The status of a single myosin head was modeled to alternate between a non–force-producing detached (D) state and a force-producing attached (A) state. A period of 1.1 s was simulated and broken into increments of equal duration, tinc = 10−4 s. When the myosin head was in the D state, the probability of transitioning to the A state within tinc was calculated as 1 − exp(−f0 × tinc), where f0 = attachment rate in units of s−1. The transition at any time increment occurred when a uniformly distributed random number, n, generated in the range 0 ≤ n < 1 was less than the calculated transition probability. Upon transitioning from D to A, an initial displacement xinit was randomly generated according to a Gaussian distribution with 0 mean and 5 nm SD and assigned to the myosin head. This initial displacement was then apprised with each time increment according to the simulated length change of the half-sarcomere so that displacement of the myosin head x = xinit + L(t). For quick stretch length changes, maximum length change was 10 nm or 1% of a 1.0-µm half-sarcomere over 2 ms. When the myosin head was in the A state, the probability of transitioning to D within tinc was calculated as 1 − exp[− (g0 + g1x) × tinc], where g0 = detachment rate in s−1 and g1 = sensitivity of detachment rate to crossbridge displacement in s−1 · nm−1. All spatial displacements and probabilities were characterized with double-precision floating point variables.
Fitting mathematical model to recorded data
Supplemental derivation of mathematical model
The conceptual model described above lends itself to an analytical solution. The derivation and explicit assumptions that lead to the analytical solution are presented in the Supplemental text (see bottom of PDF). The results of the model are presented in the text below.
Online supplemental material
Supplemental text presents the derivation and explicit assumptions that led to the analytical solution.
Results
Interpretations of the force response to a step-length change
Characteristics of myofilament function in striated muscle are often assessed in vitro by recording tensile force measured at one end of a muscle strip preparation in response to a quick step-length change applied at the other end (Fig. 1 A and inset). After normalizing force to cross-sectional area and length to resting ML, the change in stress caused by the imposed strain characterizes the dynamic stiffness, i.e., viscoelasticity, of the muscle. A typical step force response in submaximally Ca2+-activated demembranated human myocardium is shown in Fig. 1 B. It has been suggested that the instantaneous force rise (phase 1), then rapid force decay (phase 2), followed by a slowly rising (phase 3) and elevated (phase 4) force are due to stretching of attached myosin crossbridges (phase 1) and detachment of these stretched crossbridges at an exponential decay rate (phase 2), followed by crossbridges reattaching but in increased numbers due to an enhanced activation of the thin filament (phases 3 and 4; Campbell, 1997; Campbell and Chandra, 2006). These measures are often conducted at a sarcomere length that maximizes the overlap of the thick and thin filaments, such as 2.2 µm used here, thereby optimizing any interfilament interaction.
Example force response to a quick stretch. (A) This assay entails the application of a step-length change on the order of <1% resting ML. In this example, the ML between the clips (inset) was 310 µm, and a step-length change (ΔL) of 3.1 µm was applied and normalized to ML to provide strain. Force (F) was recorded and normalized to CSA to provide stress. More than 95% of the length step was achieved in <4 ms, and thus was considered a quick stretch. (B) At submaximal Ca2+ activation, the step force response of skinned human myocardium displays the four phases typically observed. These phases are most often attributed to the stretch of attached myosin crossbridges (phase 1) and gradual detachment of the stretched crossbridges (phase 2), followed by enhanced thin filament activation resulting in a gradual rise (phase 3) and maintenance (phase 4) of an elevated force. (C) An elevated force is also observed under relaxed conditions with no myosin crossbridges formed, i.e., pCa 8 + BDM. The change in stress associated with this relaxed response would be expected to accompany the activated response. (D) The crossbridge-dependent response is calculated here as the activated recording minus the relaxed recording. The resulting crossbridge-dependent stress after stretch dips below the prestretch stress for a short period between phases 2 and 3. We propose that a transient depression of contractile force underlies the nadir of phases 2 and 3.
Example force response to a quick stretch. (A) This assay entails the application of a step-length change on the order of <1% resting ML. In this example, the ML between the clips (inset) was 310 µm, and a step-length change (ΔL) of 3.1 µm was applied and normalized to ML to provide strain. Force (F) was recorded and normalized to CSA to provide stress. More than 95% of the length step was achieved in <4 ms, and thus was considered a quick stretch. (B) At submaximal Ca2+ activation, the step force response of skinned human myocardium displays the four phases typically observed. These phases are most often attributed to the stretch of attached myosin crossbridges (phase 1) and gradual detachment of the stretched crossbridges (phase 2), followed by enhanced thin filament activation resulting in a gradual rise (phase 3) and maintenance (phase 4) of an elevated force. (C) An elevated force is also observed under relaxed conditions with no myosin crossbridges formed, i.e., pCa 8 + BDM. The change in stress associated with this relaxed response would be expected to accompany the activated response. (D) The crossbridge-dependent response is calculated here as the activated recording minus the relaxed recording. The resulting crossbridge-dependent stress after stretch dips below the prestretch stress for a short period between phases 2 and 3. We propose that a transient depression of contractile force underlies the nadir of phases 2 and 3.
Under relaxed conditions (pCa 8 + BDM), when no force-producing crossbridges are formed, the force response consists solely of an elevated force akin to phase 4 (Fig. 1 C), as would be expected from a passive viscoelastic material. This change in stress observed in the relaxed response of Fig. 1 C is expected to be present when the muscle is activated. When we subtract the stress of the relaxed condition from that of the activated condition, the crossbridge-dependent response (Fig. 1 D) drops below the prestretch isometric tension during phase 2. We argue that the nadir of phase 2 must be due to a transient drop in the number of force-producing crossbridges.
Our argument starts with consideration of phase 4 of activated muscle, which demonstrates a passive-like viscoelastic response bearing a magnitude proportional to the number of attached crossbridges. Fig. 2 A illustrates step force responses in maximally Ca2+-activated conditions (pCa 4.8) and with varying MgATP concentrations. In rigor (i.e., <0.01 mM MgATP), the force response reflects all the available myosin crossbridges formed and contributing to a power-law relaxation commonly found in passive biological tissues (Djordjević et al., 2003). The power-law relaxation of stress in response to a length step is described as Gt−k, where G = stress magnitude in units mN · mm−2, t = time, and k = dimensionless constant 0 < k < 1 that dictates the relaxation dynamics. Note that magnitude G indicates the change in stress recorded at t = 1 s. Except for some noise spikes, the fit of the recorded stress under rigor conditions to the power-law was within 2% error (Fig. 2 B). The best fit of an exponential function, ae−bt + c, was not as good. The power-law fit under relaxed conditions was also generally within 2% error (Fig. 2 B). With these results, we accept that a power-law relaxation reasonably describes the step force response of muscle when myosin crossbridges are not cycling.
Force responses to stretch under varying MgATP concentrations in skinned mouse myocardium. (A) Under maximal Ca2+ activation conditions and without MgATP (<0.01 mM, shown in black), the step force response displays the power-law relaxation common for biological tissues (fit in red). The fit to a three-parameter single exponential model appears less appropriate (dashed red). A similar power-law relaxation applies when the muscle is not activated and is bathed in BDM (shown in gray, fit in red). Phases 2 and 3 arise and display faster rates as MgATP is elevated. The stress at t = 1 s corresponds to the amplitude G of the power-law relaxation. If our rationale has merit, the ratio (GMgATP − GBDM)/(GRigor − GBDM) should be proportional to the fraction of crossbridges attached and therefore reduced with increasing MgATP, which is known to reduce the myosin crossbridge duty ratio (inset). (B) The errors associated with fitting the power-law relaxation to the responses in rigor (green) and relaxed (cyan) were, except for noise, <2%. The error associated with fitting the three-parameter single exponential model to the rigor condition (dotted green) was as high as −30% at 5 ms. (C) The power-law also fitted phase 4 at various levels of calcium activation. Full relaxation was observed at pCa 8, maximum activation at pCa 5.4. The ratio (GpCa − G8)/(G5.4 − G8) displays the sigmoidal relationship with pCa similar to, but not exactly like, that of normalized isometric tension (shown in open circles). (D) The fit of the power-law relaxation to the various pCa conditions was within 2% error for most curves and within 4% error for the worst fit. The fits of phase 4 with the power-law relaxation in these datasets suggest that phase 4 reflects a soft glassy viscoelastic response, typical of biological material, with amplitude proportional to myosin crossbridge number.
Force responses to stretch under varying MgATP concentrations in skinned mouse myocardium. (A) Under maximal Ca2+ activation conditions and without MgATP (<0.01 mM, shown in black), the step force response displays the power-law relaxation common for biological tissues (fit in red). The fit to a three-parameter single exponential model appears less appropriate (dashed red). A similar power-law relaxation applies when the muscle is not activated and is bathed in BDM (shown in gray, fit in red). Phases 2 and 3 arise and display faster rates as MgATP is elevated. The stress at t = 1 s corresponds to the amplitude G of the power-law relaxation. If our rationale has merit, the ratio (GMgATP − GBDM)/(GRigor − GBDM) should be proportional to the fraction of crossbridges attached and therefore reduced with increasing MgATP, which is known to reduce the myosin crossbridge duty ratio (inset). (B) The errors associated with fitting the power-law relaxation to the responses in rigor (green) and relaxed (cyan) were, except for noise, <2%. The error associated with fitting the three-parameter single exponential model to the rigor condition (dotted green) was as high as −30% at 5 ms. (C) The power-law also fitted phase 4 at various levels of calcium activation. Full relaxation was observed at pCa 8, maximum activation at pCa 5.4. The ratio (GpCa − G8)/(G5.4 − G8) displays the sigmoidal relationship with pCa similar to, but not exactly like, that of normalized isometric tension (shown in open circles). (D) The fit of the power-law relaxation to the various pCa conditions was within 2% error for most curves and within 4% error for the worst fit. The fits of phase 4 with the power-law relaxation in these datasets suggest that phase 4 reflects a soft glassy viscoelastic response, typical of biological material, with amplitude proportional to myosin crossbridge number.
We then asked if a power-law relaxation model could reasonably underlie phase 4 when myosin crossbridges are cycling. If so, the magnitude G describing phase 4, which can be quantified as the force recorded at t = 1 s, would be proportional to the myosin crossbridge number and duty cycle. We found that the activated stress response at 1 s above the BDM response is reduced as MgATP rises. When normalized to the total range of stresses between BDM and rigor conditions, the activated response at 1 s above the BDM stress response reaches a steady-state value of <20% when MgATP is at saturating concentrations (Fig. 2 A, inset). While we have not accounted for differences in crossbridge stiffness due to the presence or absence of nucleotide, these observations with varying MgATP are consistent with an expected reduction in myosin crossbridge duty ratio with increasing MgATP. We also found that higher pCa values led to higher values for magnitude G (Fig. 2 C). When normalized, magnitude G displayed a sigmoidal response with calcium activation like that of isometric tension (Fig. 2 C, inset). The power-law fit to the force responses under the various calcium activation conditions was within 4% error after 150 ms (Fig. 2 D). We believe it reasonable to consider phase 4 as the tail of a viscoelastic response typical of biological materials and bearing power-law relaxation with magnitude proportional to crossbridge number. Phases 2 and 3 would then reasonably represent a transient depression of force due to transient reduction in the number of force-producing myosin crossbridges.
Linearity of force response in mouse myocardium
Much of our upcoming argument is based on the premise that the force response to a stretch represents a linear system, which we demonstrate here. The two properties of the force response that demonstrate linearity are homogeneity (i.e., a change of length scales proportionally to the change of force) and additivity (i.e., multiple length changes result in the addition of the respective individual force responses). Linearity occurs, or is at least reasonably approximated, in nonlinear systems with small perturbations. We undertake here a test of a linear response for a quick stretch as well as for slower stretches up to 1% ML.
To demonstrate homogeneity, we compared the scaled responses of different length changes. Step-length changes of 0.25, 0.5, and 1.0% ML were used in these tests (Fig. 3 A). Under relaxed conditions of pCa 8 + BDM, the respective force responses were multiplied by 4, 2, and 1 and superimposed for comparison in Fig. 3 B. Except in the first 10 ms of the response, these relaxed force responses did not differ >2%. At half-maximal calcium activation pCa 5.9, the scaled force responses were superimposed (Fig. 3 C), but some differences can be seen past 10 ms. The errors in the two scaled responses corresponding to 0.25 and 0.5% length changes relative to the 1.0% response were calculated as the difference (scaled response minus 1.0% response) divided by the 1.0% force response at 1 s. Fig. 3 D illustrates that the error was <5% at almost all time points. These results suggest that the property of homogeneity is reasonably approximated to within 5% error.
Linearity of force responses to length changes. (A) To test homogeneity, three different step-length changes (0.25, 0.5, and 1% ML) were applied to the same preparation of skinned mouse myocardium. (B) Under relaxed conditions (pCa 8 + BDM), the respective force responses were multiplied by scaling factors 4, 2, and 1 and superimposed for display. There were no observable differences among the responses except in the first 10 ms (inset). (C) At half-maximal Ca2+ activation (pCa 5.9), the scaled force responses were again superimposed and are observed to be qualitatively similar. (D) Error due to scale was calculated as the difference between scaled responses (0.25 and 0.5% ML) and the 1% ML response normalized to the 1% ML force at 1 s. These errors were as high as 9% but generally no more than 5% error throughout the recorded period. (E) To test additivity, a step-length change (dashed line) and four ramp-length changes of varying durations (solid lines) were applied. Each ramp could be generated from the step using a convolution integral, whose kernel was calculated by deconvolving the first derivative of the ramp with that of the step (inset provides example for 10-ms ramp). (F) The resulting kernel (bold in inset of E) was then used to calculate theoretical force responses based on the measured step force response. Under relaxed conditions, the theoretical force responses (solid lines) were similar to the measured force responses (dots) that arose when the ramp-length changes were applied. The error between theoretical and measured responses was consistently <5% throughout the recorded period for all ramps. Inset shows examples of 10-ms ramp and 100-ms ramp in bold. (G) At half-maximal Ca2+ activation, the theoretical ramp force responses (solid lines) were visually similar to the measured ramp force responses (dots). (H) Errors were briefly as high as 8% but were generally no more than 5% throughout the recorded period. These demonstrations suggest that the mechanical response of relaxed and activated mouse myocardium to step- and ramp-length changes can be approximated as linear.
Linearity of force responses to length changes. (A) To test homogeneity, three different step-length changes (0.25, 0.5, and 1% ML) were applied to the same preparation of skinned mouse myocardium. (B) Under relaxed conditions (pCa 8 + BDM), the respective force responses were multiplied by scaling factors 4, 2, and 1 and superimposed for display. There were no observable differences among the responses except in the first 10 ms (inset). (C) At half-maximal Ca2+ activation (pCa 5.9), the scaled force responses were again superimposed and are observed to be qualitatively similar. (D) Error due to scale was calculated as the difference between scaled responses (0.25 and 0.5% ML) and the 1% ML response normalized to the 1% ML force at 1 s. These errors were as high as 9% but generally no more than 5% error throughout the recorded period. (E) To test additivity, a step-length change (dashed line) and four ramp-length changes of varying durations (solid lines) were applied. Each ramp could be generated from the step using a convolution integral, whose kernel was calculated by deconvolving the first derivative of the ramp with that of the step (inset provides example for 10-ms ramp). (F) The resulting kernel (bold in inset of E) was then used to calculate theoretical force responses based on the measured step force response. Under relaxed conditions, the theoretical force responses (solid lines) were similar to the measured force responses (dots) that arose when the ramp-length changes were applied. The error between theoretical and measured responses was consistently <5% throughout the recorded period for all ramps. Inset shows examples of 10-ms ramp and 100-ms ramp in bold. (G) At half-maximal Ca2+ activation, the theoretical ramp force responses (solid lines) were visually similar to the measured ramp force responses (dots). (H) Errors were briefly as high as 8% but were generally no more than 5% throughout the recorded period. These demonstrations suggest that the mechanical response of relaxed and activated mouse myocardium to step- and ramp-length changes can be approximated as linear.
To demonstrate additivity, we tested if a convolution integral applied to the step length would produce a theoretical force response similar to an actual force response. Fig. 3 E illustrates a step-length change of 1% ML (dashed line) and four ramp length changes to 1% ML over 10, 20, 50, and 100 ms (solid lines), respectively. The first derivatives of the step and of each ramp were compared to each other, resulting in a convolution kernel (Fig. 3 E, inset), which when convolved with the original length step reproduces the ramp. That same kernel was then convolved with the step force response to produce a theoretical force response to the ramp.
The additivity test when the muscle is not activated at pCa 8 + BDM suggests linearity (Fig. 3 F). The original step force response (dashed line) was convolved with the four respective kernels to produce four theoretical ramp force responses (solid lines). The measured, actual ramp force responses are overlaid (dotted line). The differences between the theoretical and actual ramp force responses were normalized to the force at 1 s to quantify discrepancies as percentage error. The error between theoretical and actual was consistently <5% throughout the time period examined for all ramps, as illustrated in Fig. 3 F (inset) for 10- and 100-ms ramps. These results demonstrate that the force response of relaxed muscle due to a ramp length change displays the additive property of multiple length perturbations as represented in the convolution kernel.
The additivity test for muscle activated at pCa 5.9 also suggests linearity (Fig. 3 G). The original force response (dashed line) was convolved with the respective kernels to produce the theoretical ramp force responses (solid lines), and the measured force responses are overlaid (dotted line). Errors between theoretical and actual force responses for all four ramp length changes were <10% over the entire time duration recorded and <5% for all but a 10–20-ms portion (Fig. 3 H). Notably, error associated with the 100-ms range was <5% for the entire time period.
The tests of linearity demonstrate that the mechanical properties of both relaxed and activated mouse myocardium under the conditions noted here are reasonably linear to within 5–10% error for length changes of ≤1% ML. For the remainder of this paper, we will assume approximate linearity, which allows us to produce a linear mathematical model and perform further calculations of power and energy required to elongate mouse myocardium.
Modeling force response with strain-dependent myosin crossbridge kinetics
Power-law relaxation
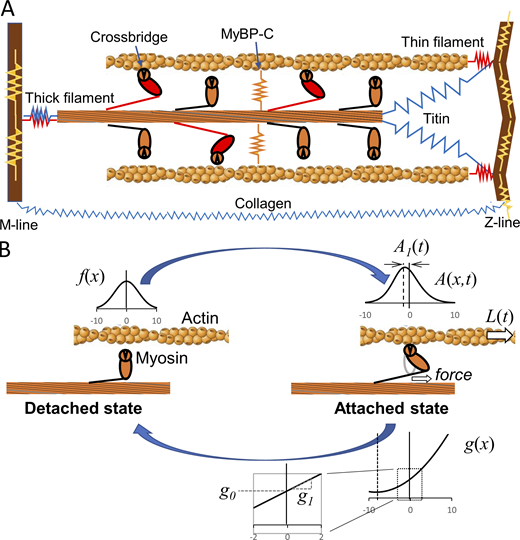
Cartoon illustration of the half sarcomere and a two-state model of myosin crossbridge formation.(A) Those protein connections that span the half sarcomere and are responsible for crossbridge-independent viscoelasticity include most notably titin and collagen (blue). Protein connections responsible for crossbridge-dependent viscoelasticity include myosin and other proteins of the thick and thin filaments and the M- and Z-lines such as actin, α-actinin, etc. (red). Still other proteins, such as myosin-binding protein C, contribute to a transverse stiffness that can play indirect roles in longitudinal viscoelasticity (orange and yellow). (B) The two-state model developed here assumes a non–force-producing detached state and a force-producing attached state. The rate of transition from detached to attached is a function of x, f(x), that signifies the spatial distribution of newly formed crossbridges. This distribution is modeled as Gaussian and, importantly, evenly symmetric about a central point we define as x = 0. Crossbridges in the attached state are spatially distributed according to A(x,t), with a mean displacement that is not symmetric about x = 0 owing to the strain dependence of the detachment rate, g(x). In this example, detachment rate is modeled to be enhanced with positive strain, i.e., stretch, and reduced with negative strain, i.e., compression, as signified by the proportionality constant g1. Under no strain, the detachment rate is a constant g0.
Cartoon illustration of the half sarcomere and a two-state model of myosin crossbridge formation.(A) Those protein connections that span the half sarcomere and are responsible for crossbridge-independent viscoelasticity include most notably titin and collagen (blue). Protein connections responsible for crossbridge-dependent viscoelasticity include myosin and other proteins of the thick and thin filaments and the M- and Z-lines such as actin, α-actinin, etc. (red). Still other proteins, such as myosin-binding protein C, contribute to a transverse stiffness that can play indirect roles in longitudinal viscoelasticity (orange and yellow). (B) The two-state model developed here assumes a non–force-producing detached state and a force-producing attached state. The rate of transition from detached to attached is a function of x, f(x), that signifies the spatial distribution of newly formed crossbridges. This distribution is modeled as Gaussian and, importantly, evenly symmetric about a central point we define as x = 0. Crossbridges in the attached state are spatially distributed according to A(x,t), with a mean displacement that is not symmetric about x = 0 owing to the strain dependence of the detachment rate, g(x). In this example, detachment rate is modeled to be enhanced with positive strain, i.e., stretch, and reduced with negative strain, i.e., compression, as signified by the proportionality constant g1. Under no strain, the detachment rate is a constant g0.
Example components of our model describing the step force response of activated muscle to a quick stretch.(A) A power-law relaxation after a quick stretch, σp(t), is used to represent phase 4. (B) The mean crossbridge displacement A1(t) is a negative value until the step, which imposes a positive-going mean displacement. The positive displacement is then relaxed with a rate constant of g0. The stress due to the displacement of crossbridges, σ1(t), is on the order of mN · mm−2 in this example. (C) The positive mean displacement shown in B leads to a higher probability of crossbridge detachment according to g(x) resulting in a transiently reduced equilibrium point (dotted line) and transient reduction in the fraction of crossbridges attached, A0(t), attempting to reach equilibrium. The stress attributable to the fraction of crossbridges formed, σ0(t), is on the order of tens of mN · mm−2 in this example. (D) All components together generate a step force response similar in shape to that recorded with a muscle sample. Parameters used to generate this figure were f0 = 25 s−1, SD of f(x) distribution = 5 nm, f2 = 625 s−1 · nm2, g0 = 50 s−1, g1 = 2 s−1 · nm−1, N = 1013 available myosin, CSA = 1 mm2, kstiff = 0.15 pN · nm−1, ΔL = 10 nm, Lhs = 1,000 nm, Funi = 10 pN, σrest = 3 mN · mm−2, Gp = 20 mN · mm−2, and kp = 0.15 (unitless).
Example components of our model describing the step force response of activated muscle to a quick stretch.(A) A power-law relaxation after a quick stretch, σp(t), is used to represent phase 4. (B) The mean crossbridge displacement A1(t) is a negative value until the step, which imposes a positive-going mean displacement. The positive displacement is then relaxed with a rate constant of g0. The stress due to the displacement of crossbridges, σ1(t), is on the order of mN · mm−2 in this example. (C) The positive mean displacement shown in B leads to a higher probability of crossbridge detachment according to g(x) resulting in a transiently reduced equilibrium point (dotted line) and transient reduction in the fraction of crossbridges attached, A0(t), attempting to reach equilibrium. The stress attributable to the fraction of crossbridges formed, σ0(t), is on the order of tens of mN · mm−2 in this example. (D) All components together generate a step force response similar in shape to that recorded with a muscle sample. Parameters used to generate this figure were f0 = 25 s−1, SD of f(x) distribution = 5 nm, f2 = 625 s−1 · nm2, g0 = 50 s−1, g1 = 2 s−1 · nm−1, N = 1013 available myosin, CSA = 1 mm2, kstiff = 0.15 pN · nm−1, ΔL = 10 nm, Lhs = 1,000 nm, Funi = 10 pN, σrest = 3 mN · mm−2, Gp = 20 mN · mm−2, and kp = 0.15 (unitless).
Strain-dependent crossbridge kinetics
The conceptual model we consider is a two-state model in which the myosin head is in either a strongly bound force-producing state or a weakly bound non–force-producing state. The spatial distribution of newly formed strongly bound crossbridges is given by f(x), which we assume to be symmetrical about x = 0, and represents the myosin-binding site on the thin filament relative to a nondisplaced myosin head emanating from the thick filament. The term f0 = total attachment rate, i.e., integral of f(x) over all x, in units of s−1. We also include an explicit strain dependence on the detachment rate, g(x) = g0+ g1x, where g0 = detachment rate of an unstrained crossbridge in s−1 and g1 = sensitivity of detachment rate to crossbridge displacement in s−1 · nm−1 (Fig. 4 B). The positive sign associated with g1 signifies that detachment rate g(x) is enhanced with muscle lengthening. The Supplemental text (see bottom of PDF) presents a full derivation of the mathematical model. The key results are presented here.
Full step response
Fitting the model to recorded data
Using the analytical solution provided in Eq. 7, we estimated the model parameters that generated the best fits to step force responses collected in skinned mouse myocardial strips activated at pCa 5.9 and exposed to increasing Pi. We observed that isometric stress before stretch was correspondingly reduced from 18.1 to 16.4 mN · mm2 as Pi was raised from 1 to 8 mM (Smith and Geeves, 1995; Ranatunga, 1999). For our purposes, the isometric stress was subtracted from recorded stress, and the change in stress, Δσ, was examined as a reflection of myocardial viscoelasticity. Fig. 6 A illustrates the force responses recorded for 1, 3, and 8 mM Pi. For almost all muscles examined, the magnitude of phase 4 was reduced with increasing Pi. However, we focused on this dataset specifically because of the similarities in phase 4 among the different Pi conditions. The consequences of Pi on myosin crossbridge kinetics are then readily observed in phases 2 and 3. The fits of Eq. 7 to Δσ are superimposed on the recorded data, and parameter estimates are given in Table 1. We then assessed the results of the fits and the reasonableness of the model parameters.
Results of fits of the model to recorded step force responses. (A) With varying Pi, the analytical model (solid lines) fits the step force responses well. (B) The power-law relaxation component appears little affected by varying Pi in these examples. (C) According to model fits, the mean displacement of crossbridges and corresponding stress (Δσ1) was reduced in magnitude and quicker to relax with higher Pi, which is expected. (D) The fraction of crossbridges attached and corresponding stress shown (Δσ0) demonstrated a reduced nadir with higher Pi. This finding would suggest that the higher Pi led to higher rate constants in such a way as to reduce the force drop between phases 2 and 3.
Results of fits of the model to recorded step force responses. (A) With varying Pi, the analytical model (solid lines) fits the step force responses well. (B) The power-law relaxation component appears little affected by varying Pi in these examples. (C) According to model fits, the mean displacement of crossbridges and corresponding stress (Δσ1) was reduced in magnitude and quicker to relax with higher Pi, which is expected. (D) The fraction of crossbridges attached and corresponding stress shown (Δσ0) demonstrated a reduced nadir with higher Pi. This finding would suggest that the higher Pi led to higher rate constants in such a way as to reduce the force drop between phases 2 and 3.
Parameter estimates resulting from fitting Eq. 7 to step force responses recorded in skinned mouse myocardium exposed to varying Pi at approximately half Ca2+ activation, pCa 5.9
| Condition . | Gp (mN · mm−2) . | kp . | (mN · mm−2) . | (mN · mm−2) . | f0 + g0 (s−1) . | g0 (s−1) . | f0 (s−1) . |
|---|---|---|---|---|---|---|---|
| [Pi] (mM) | |||||||
| 1.0 | 142 | 0.154 | 37.2 | 3.25 | 80.6 | 67.2 | 13.4 |
| 2.0 | 139 | 0.159 | 35.4 | 2.91 | 84.3 | 70.1 | 14.2 |
| 3.0 | 141 | 0.154 | 34.2 | 2.78 | 86.4 | 71.9 | 14.5 |
| 4.0 | 143 | 0.149 | 36.6 | 2.53 | 89.3 | 75.9 | 13.4 |
| 5.0 | 139 | 0.157 | 38.2 | 2.21 | 90.3 | 77.7 | 12.6 |
| 8.0 | 144 | 0.148 | 49.2 | 2.43 | 93.6 | 83.1 | 10.5 |
| r | 0.527 | −0.587 | 0.842 | −0.808 | 0.962 | 0.990 | −0.862 |
| P | 0.283 | 0.288 | 0.036 | 0.049 | 0.002 | <0.001 | 0.027 |
| Condition . | Gp (mN · mm−2) . | kp . | (mN · mm−2) . | (mN · mm−2) . | f0 + g0 (s−1) . | g0 (s−1) . | f0 (s−1) . |
|---|---|---|---|---|---|---|---|
| [Pi] (mM) | |||||||
| 1.0 | 142 | 0.154 | 37.2 | 3.25 | 80.6 | 67.2 | 13.4 |
| 2.0 | 139 | 0.159 | 35.4 | 2.91 | 84.3 | 70.1 | 14.2 |
| 3.0 | 141 | 0.154 | 34.2 | 2.78 | 86.4 | 71.9 | 14.5 |
| 4.0 | 143 | 0.149 | 36.6 | 2.53 | 89.3 | 75.9 | 13.4 |
| 5.0 | 139 | 0.157 | 38.2 | 2.21 | 90.3 | 77.7 | 12.6 |
| 8.0 | 144 | 0.148 | 49.2 | 2.43 | 93.6 | 83.1 | 10.5 |
| r | 0.527 | −0.587 | 0.842 | −0.808 | 0.962 | 0.990 | −0.862 |
| P | 0.283 | 0.288 | 0.036 | 0.049 | 0.002 | <0.001 | 0.027 |
The correlation coefficient, r, refers to the Pearson coefficient between the given parameter and Pi condition; r values shown in bold demonstrate statistical significance at P < 0.05.
Power-law relaxation
The power-law relaxation component of the force response, Δσp, did not appreciably differ among the three Pi concentrations as selected and therefore are indistinguishable in Fig. 6 B. The modulus Gp and viscous-elastic ratio kp that describe the power-law relaxation characteristic were not found to be dependent on Pi in these examples (correlation coefficients = 0.527 and −0.587, respectively, were not statistically significant; Table 1).
Mean displacement of attached crossbridges
The mean displacement of crossbridges due to stretch results in the stress Δσ1 (Fig. 6 C). This component of the force response corresponds to the elastic force generated from the initial stretch of crossbridges and the exponential decay of that force as these crossbridges detach. The interpretation of this component of the force response appearing in several previous models would seem intuitively appropriate (Kawai and Brandt. 1980; Palmer et al., 2007).
The decay rate shown in Fig. 6 C, which corresponds to g0, is enhanced with higher Pi (supported by a correlation coefficient = 0.990 in Table 1), which would be expected if Pi facilitates detachment before MgADP release. It is noteworthy that the amplitude of Δσ1, directly proportional to parameter , is reduced with increasing Pi (correlation coefficient = −0.808 in Table 1), which is consistent with Pi enhancing the detachment rate under steady-state conditions. So far, we would infer that our modeling of mean displacement of attached crossbridges corresponds to the expected effects of Pi.
Fraction of crossbridges attached
Stress, power, and energy required to elongate myocardium
To demonstrate that the stretch-enhanced detachment of myosin results in reduced resistance to myocardial lengthening, we modeled the length change experienced by ventricular myocardium during diastole as a 1% ML change over 100 ms (Fig. 7 A). We then generated the total stress response, Δσ, for 1, 3, and 8 mM Pi (Fig. 7 B) from the respective step force responses convolved with the 100-ms kernel described earlier in Fig. 3 E. The stress changes shown in Fig. 7 B represent the muscle responses to a constant length change over 100 ms. The hypothetical power-law response displayed in Fig. 7 B corresponds to the power-law relaxation calculated for phase 4 in Fig. 6 B that would arise if there were no transient reduction in force, i.e., if there were no phases 2 and 3. The comparison with the hypothetical power-law response demonstrates that the transient depression in force, as we hypothesize occurs with an enhanced detachment rate during lengthening, would result in a lower stress required to achieve the ramp lengthening profile over 100 ms.
Stress, power, and energy required to stretch 1% ML over 100 ms, which mimics late diastolic filling. (A) A strain of 1% ML is applied over 100 ms. The strain rate is ∼0.1 ML/s over the same 100 ms. (B) The stress required to stretch the muscle 1% over 100 ms, reflected in Δσ(t), is compared against the hypothetical power-law response extrapolated from the fit to phase 4. With myosin detachment enhanced by stretch, the stress required to stretch the muscle is reduced compared with the hypothetical power-law response. (C) The mechanical power per muscle volume required to stretch the muscle 1% over 100 ms was calculated as the product of stress and strain rate. The power required to stretch the muscle was reduced compared with the hypothetical power-law response. (D) The mechanical energy per muscle volume required to stretch the muscle 1% over 100 ms is lowered by ∼25% compared with the hypothetical power-law response. The total energy required to perform this stretch is lower for 3 mM Pi compared with 1 mM but is highest for 8 mM (inset). This comparison demonstrates that faster myosin kinetics do not necessary lead to more favorable energy expenditure.
Stress, power, and energy required to stretch 1% ML over 100 ms, which mimics late diastolic filling. (A) A strain of 1% ML is applied over 100 ms. The strain rate is ∼0.1 ML/s over the same 100 ms. (B) The stress required to stretch the muscle 1% over 100 ms, reflected in Δσ(t), is compared against the hypothetical power-law response extrapolated from the fit to phase 4. With myosin detachment enhanced by stretch, the stress required to stretch the muscle is reduced compared with the hypothetical power-law response. (C) The mechanical power per muscle volume required to stretch the muscle 1% over 100 ms was calculated as the product of stress and strain rate. The power required to stretch the muscle was reduced compared with the hypothetical power-law response. (D) The mechanical energy per muscle volume required to stretch the muscle 1% over 100 ms is lowered by ∼25% compared with the hypothetical power-law response. The total energy required to perform this stretch is lower for 3 mM Pi compared with 1 mM but is highest for 8 mM (inset). This comparison demonstrates that faster myosin kinetics do not necessary lead to more favorable energy expenditure.
Mechanical power is defined as the product of the stress and strain rate. The mechanical power per volume of muscle sample that must be applied to the muscle to achieve the 1% length change can therefore be easily calculated from stress and strain rate (Fig. 7 C). The mechanical energy per sample volume is then calculated as the time integral of the power (Fig. 7 D). The inset of Fig. 7 D illustrates that the energy required to perform the 100-ms stretch was lower at 3 mM Pi compared with 1 mM, but higher at 8 mM. This result demonstrates that the energy expenditure for a stretch depends on many factors that make up the muscle viscoelasticity, including myosin kinetics, stretch speed, and stretch duration. In short, faster myosin kinetics do not necessarily lead to less energy expenditure.
It should be noted that these calculations of stress, power, and energy are not based on our model. Only the hypothetical power-law responses shown throughout Fig. 7 result from the power-law model of phase 4. In all these examples, the stress, power, and energy required to elongate the muscle 1% ML over 100 ms are lower than that required from the hypothetical power-law response.
Computer simulation of stretch
We used a computer model to estimate the effects of a length change on the number of myosin crossbridges attached or detached over the course of a prolonged stretch. Both early and late filling periods last ∼100 ms in healthy adults and stretch the circumference of the ventricle on the order of an additional 1–20% (Zhang et al., 2019). In our experience, the characteristic time points of a force response due to α-myosin kinetics in mouse myocardium at 17°C are roughly those of β-myosin kinetics in human myocardium at 37°C (unpublished data). Therefore, for illustrative purposes, we modeled the effects of a 1% stretch over 100 ms using parameters suggested from the fit of the model to the data recorded from mouse myocardium under the 17°C and 1-mM Pi conditions (Fig. 8 A).
Results of computer simulation of muscle force response to a 1% stretch over 100 ms. (A) The strain in this case is a perfect ramp to 1% strain over 100 ms. The strain rate is a constant 0.1 ML/s over that period. (B) The states, either attached or detached, of 5 million myosin heads were simulated using rate constants estimated from the case of 1 mM Pi in real muscle (Fig. 5 B and Table 1). (C) The enhanced detachment rate with strain on the crossbridge resulted in a reduced fraction of force-producing crossbridges attached and an enhanced fraction of detached during and immediately after the stretch. This result suggests that an enhanced crossbridge detachment rate with stretch can explain the enhanced relaxation during stretch (Chung et al., 2017). (D) An enhanced detachment rate with stretch would permit stretch with less mechanical energy compared with the hypothetical power-law response. Parameters used in this simulation were f0 = 13.4 s−1, SD of f(x) = 2 nm, f2 = 53.6 s−1 · nm2, g0 = 67.2 s−1, g1 = 6 s−1 · nm−1, N = 1010 available myosin per half sarcomere · mm−2, CSA = 1 mm2, kstiff = 0.3 pN · nm−1, ΔL = 10 nm, Lhs = 1,000 nm, Funi = 10 pN, σrest = 0 mN · mm−2, Gp = 142 mN · mm−2, and kp = 0.154 (unitless).
Results of computer simulation of muscle force response to a 1% stretch over 100 ms. (A) The strain in this case is a perfect ramp to 1% strain over 100 ms. The strain rate is a constant 0.1 ML/s over that period. (B) The states, either attached or detached, of 5 million myosin heads were simulated using rate constants estimated from the case of 1 mM Pi in real muscle (Fig. 5 B and Table 1). (C) The enhanced detachment rate with strain on the crossbridge resulted in a reduced fraction of force-producing crossbridges attached and an enhanced fraction of detached during and immediately after the stretch. This result suggests that an enhanced crossbridge detachment rate with stretch can explain the enhanced relaxation during stretch (Chung et al., 2017). (D) An enhanced detachment rate with stretch would permit stretch with less mechanical energy compared with the hypothetical power-law response. Parameters used in this simulation were f0 = 13.4 s−1, SD of f(x) = 2 nm, f2 = 53.6 s−1 · nm2, g0 = 67.2 s−1, g1 = 6 s−1 · nm−1, N = 1010 available myosin per half sarcomere · mm−2, CSA = 1 mm2, kstiff = 0.3 pN · nm−1, ΔL = 10 nm, Lhs = 1,000 nm, Funi = 10 pN, σrest = 0 mN · mm−2, Gp = 142 mN · mm−2, and kp = 0.154 (unitless).
A computer simulation of the fraction of myosin heads attached and detached showed that the fraction of myosin heads in the attached state is reduced with imposed constant strain rate on the muscle and reaches a lower steady-state value within ∼50 ms (Fig. 8 B). This lower number of crossbridges during a steady lengthening was predicted previously by Smith and Geeves (1995). Conversely, the fraction of detached myosin heads is elevated with the same magnitude and dynamics. These changes in the fractions of heads attached and detached result from the enhanced detachment rate of the myosin crossbridges as they experience increasingly greater strain during the simulated stretch.
After applying the necessary constants to express stress as would be recorded from a muscle, we simulated the stress response and its components (Fig. 8 C). The stress σ1(t) due to the mean displacement A1(t) is small and negative valued before stretch, because there is a bias for longer-lived crossbridges with negative strain. The values of σ1(t) and A1(t) then become positive at a maximum of ∼0.5 mN · mm−2 during the imposed constant strain rate. This stress corresponds to the elastic recoil force that arises from the stretching of attached myosin crossbridges. The stress σ0(t) due to the fraction of crossbridges attached A0(t) and generating Funi is reduced as the number of attached crossbridges is reduced during the period of imposed constant strain rate. This reduction in the number of force-generating crossbridges illustrates that an enhanced detachment rate due to strain on the crossbridge could account for a transient loss of crossbridge number. The stress σp(t) due to the power-law relaxation of the muscle reflects the expected power-law stress relaxation that would be expected to occur if there were no change in detachment rate with strain (Fig. 8 C). A hypothetical power-law response, which reflects the response expected if there were no change in detachment rate with strain (dotted line in Fig. 8 D), i.e., σrest + σp(t), is also shown for comparison purposes.
The total stress response, i.e., the sum σ1(t) + σ0(t) + σp(t), that resulted from the computer model is qualitatively similar in dynamics to that recorded from real mouse myocardium (Fig. 3 G). When compared with the hypothetical power-law response, it is clear that the stretch of the muscle is accomplished with less stress when an enhanced detachment rate due to strain is available. Consequently, the total energy required to stretch the myocardium 1% over 100 ms (Fig. 8 D) would also be reduced when the myosin detachment rate is enhanced with strain.
Discussion
Our study demonstrates that a strain-dependent enhancement of myosin crossbridge detachment sufficiently explains the step force response observed in cardiac muscle after a quick stretch. It should be noted that we have not proven this to be the case, only that it is plausible. Our findings suggest that phases 2 and 3 of the typical step force response could arise from a transiently reduced myofilament force due to a briefly enhanced crossbridge detachment rate caused by strain on those crossbridges already attached when stretch occurs followed by their reattachment. We further suggest that the elevated force of phase 4 does not reflect a stretch activation of the thin filament, but rather the tail of a power-law viscoelastic response commonly found in biological tissues. Our interpretation differs significantly from conventional interpretations of these data and, therefore, could offer novel insights into the physiological mechanisms that underlie diastolic function in mammalian cardiac muscle.
The prevailing interpretation of the force response to a quick stretch has centered on the enhanced activation of the thin filament regulatory proteins, troponins and tropomyosin, due to the strain experienced during and after a stretch (Campbell, 1997; Moss et al., 2004; Campbell and Chandra, 2006; Stelzer and Moss, 2006). This enhanced activation of the thin filament due to stretch may play some role in cardiac muscle as it does in insect flight muscle, where the activating and deactivating movements of troponins and tropomyosin can be elicited by a 2% stretch (Perz-Edwards et al., 2011). However, thin-filament regulatory proteins are not required to induce the typical step force response in mammalian cardiac muscle. In a series of studies by Kawai and colleagues, bovine cardiac muscle lacking thin-filament regulatory proteins still displayed the characteristic features expected of a typical step force response. Specifically, after thin filaments were removed and actin filaments were reconstituted without regulatory proteins, the complex modulus detected using sinusoidal analysis displayed (a) the prominent peak in the viscous modulus at high frequencies, corresponding to phase 2, (b) the prominent negative viscous modulus at low frequencies, corresponding to phase 3, and (c) positive-valued elastic and viscous moduli at the lowest frequency, corresponding to phase 4 (Fujita and Kawai, 2002; Fujita et al., 2002; Lu et al., 2005; Kawai and Ishiwata, 2006). Thus, an effect of stretch on the thin filament is not necessary to invoke as the primary underlying mechanism of the force response to stretch. We hypothesized instead that the typical force response to a quick stretch is due to the enhanced detachment rate in those crossbridges that were under strain.
Using a two-state model, we have not assigned or assumed where in the crossbridge cycle a strain due to stretch could influence myosin detachment rate. It is reported that the rate of MgADP release in cardiac myosin and in smooth muscle myosin, another class II myosin like cardiac myosin, is slowed by a resistive load, which corresponds to muscle stretch (Veigel et al., 2005; Kad et al., 2007; Liu et al., 2018). In the context of those findings, our results would suggest that enhanced detachment with stretch must occur before MgADP release. Such a strain-dependent detachment could involve reversal of the myosin power stroke, which has been observed and modeled to be sensitive to Pi availability (Dantzig et al., 1992; Smith and Geeves, 1995), or possibly without reversal but still sensitive to Pi (Debold et al., 2013). Other observations consistent with either mechanism include a Pi-enhanced rate of tension development after rapid temperature change (Ranatunga, 1999), a significantly shorter myosin crossbridge lifetime observed in the laser trap assay when Pi is abundant (Baker et al., 2002), a reduced rate of free Pi generation in activated striated muscle undergoing stretch (Mansfield et al., 2012), and an enhanced oscillatory work and power with increasing Pi (Zhao and Swank, 2013).
Our own observations with increasing Pi concentration are consistent with the idea that Pi acts to enhance crossbridge detachment rate, i.e., g0 in our model, as noted by a positive correlation between g0 and Pi in Table 1. Because g0 also incorporates detachment due to MgATP binding in our two-state model, we surmise that the two-state model, while useful in the present demonstration, is not adequate to describe the full interplay between biochemical and mechanical influences on myosin crossbridge kinetics. We would need at least two force-producing states in future modeling efforts relevant to conditions with saturating MgATP. With at least two force-producing states, the rate of reversal could be made explicitly dependent on Pi availability and the strain imposed on the crossbridge during lengthening, as proposed previously (Dantzig et al., 1992; Smith and Geeves, 1995; Ranatunga, 1999; Houdusse and Sweeney, 2001; Zhao and Swank, 2013). Such a mechanism would have significant implications for our understanding of striated muscle relaxation function, including cardiac diastole.
Relevance to diastolic function
Ventricular diastole can be considered to occur in four phases: isovolumic relaxation, early filling, diastasis (when little filling occurs), and late filling. Isovolumic relaxation commences when the aortic valve closes as myocardial contractile force subsides with diminishing intracellular Ca2+ activation of contractile force. During this phase, the ventricular myocardium, which had been compressed during systole, begins to rebound due to stored elastic energy. The latter causes shape changes during this phase, but overall relengthening cannot begin until the mitral valve opens. This occurs when the LV pressure falls below the left atrium (LA) pressure, and early filling ensues. During early filling, the ventricular myocardium undergoes overall relengthening driven by the stored elastic energy, which produces a suction that draws blood into the enlarging LV from the LA, as well as by the level of LA pressure at the time of mitral valve opening (Bell et al., 2000). Early filling is not considered an energy-consuming process and accounts for as much as ∼80% of the end-diastolic volume of the normal human adult LV (Zhang et al., 2019). Once LV and LA pressures equilibrate, early filling ceases and a diastatic phase commences with little or no filling. The length of this phase is variable and largely dependent on heart rate. Late filling then occurs when the LA actively pumps blood into the LV immediately before ventricular systole. In a normal human adult LV, the endocardium may lengthen an additional 4–6% and the epicardium 1–3% over a span of ∼100 ms during late filling (Zhang et al., 2019). This seemingly small percentage change in myocardial length represents as much as ∼ 20% increase in chamber volume and plays an important part in normal LV filling.
If the LV myofilaments produce contractile force at any time during diastole, due to the normal basal level of Ca2+-independent activation of the thin filament observed in human myocardium (Donaldson et al., 2012) or due to incomplete removal of intracellular Ca2+ as observed in normal and more so in hypertrophied human LV (Selby et al., 2011; Runte et al., 2017), the myocardium will resist lengthening, and end-diastolic chamber volume may not reach its fullest extent before systole begins. In this way, a persistent contractile force produced by myosin crossbridges contributes to the viscoelastic stiffness of ventricular myocardium throughout diastole and thereby plays a significant role in diastolic dysfunction.
With an important set of observations, Chung et al. (2017) reported that lengthening the myocardium at the end of systole enhanced relaxation in proportion to the rate of relengthening. These findings mirror those reported in a whole heart, which experienced faster relaxation when load on the LV was artificially enhanced in late systole (Zile and Gaasch, 1991). Those observations, like ours, were made at the macroscopic level, where relengthening in diastole takes place with a strain rate over time periods lasting up to 100 ms. The myosin crossbridge is relatively short-lived, on the order of 10–40 ms on average (Tyska and Warshaw, 2002). Therefore, an attached myosin crossbridge would experience significant strain during diastolic relengthening and would be subjected to any strain dependence on its kinetics.
The mitigation of crossbridge force during increasing myocardial strain rate due to the underlying myosin crossbridge strain may be an important contributor to filling function in all phases of diastole, because some level of thin filament activation persists throughout diastole. A measurable myofilament force is produced in human myocardium at normal and elevated diastolic Ca2+ (Selby et al., 2011; Runte et al., 2017) and at nonactivating Ca2+ concentrations (Gong et al., 2005; Donaldson et al., 2012). Strongly bound myosin crossbridges can also contribute to thin filament activation due to elevated MgADP, which can accompany and compound heart failure (Sequeira et al., 2015). Therefore, either with or without compromised calcium ion handling, some level of contractile force is present throughout diastole (Moss et al., 2004) and would contribute to myocardial stiffness and oppose LV myocardial lengthening and chamber filling. The findings of Chung et al. (2017) and Zile and Gaasch (1991) would therefore be applicable throughout diastole, including late diastole. A reversal of the myosin power stroke, as we have proposed here in response to a positive strain (or resistive load) on the crossbridge, would reduce myocardial stiffness and ease ventricular filling as well as reduce unnecessary utilization of MgATP. The reversal of the power stroke during stretch would ensure, or at least bias, that the energy liberated from MgATP hydrolysis is not used during stretch but rather during shortening. Such a mechanism would seem energetically and evolutionarily beneficial.
In the model presented in this paper, the nadir of the force response to a quick stretch reflects an enhanced detachment rate caused by stretch. The depth of this nadir, and therefore the energetic savings afforded by the underlying mechanism, is directly dependent on the sensitivity of crossbridge detachment rate to crossbridge displacement, g1. We expect that this sensitivity constant is defined in part by the amount of deformation experienced by the myosin head and the enhanced probability of power stroke reversal with or without Pi binding. The deformation of the myosin head is further dependent on its mechanical compliance relative to other sarcomeric structures bearing load. The various isoforms, mutations, and phosphorylation statuses of all sarcomeric proteins (actin, titin, myosin-binding protein C, tropomyosin, troponins, etc.) can also modulate the probability of power stroke reversal via their influence on relative sarcomere stiffness, which affects myosin head deformation during stretch. We suspect that slow myosin isoforms provide greater opportunity for power stroke reversal due to the slower MgADP release rate and higher sensitivity to Pi compared with the faster myosin isoforms, as demonstrated in skeletal muscle (Straight et al., 2019). In human cardiac muscle, the slower β-myosin may similarly better suit LV relaxation compared with the faster α-myosin isoform.
Limitations
We have not explained the molecular mechanisms that underlie the power-law relaxation used to fit phase 4. We note that the magnitude of phase 4, measured at t = 1 s, is proportional to crossbridge number as manipulated by MgATP or activating Ca2+ concentration. However, at saturating MgATP, the crossbridges that were initially stretched at time 0, modeled as A1(t), are detached and reattached at new positions within 100 ms and would not directly participate in the elevated stress at t = 1 s. How then can the magnitude of phase 4 be proportional to crossbridge number but not due to the initial stretch of crossbridges? We speculate the magnitude of phase 4 reflects (a) the transverse stiffness of the sarcomere translated into longitudinal stiffness through Poisson’s ratio of the muscle, and (b) the stretched proteins that are in series with the crossbridges, including those that anchor the myofilaments to the M- and Z-lines; both cases would be proportional to crossbridge number and not dependent on those crossbridges initially stretched. Further work is warranted in elucidating the mechanisms underlying phase 4.
Further limitations of the current work include the use of a two-state model of the myosin crossbridge, as stated above, and the use of first-order approximations used throughout our modeling. Of note, we used a constant value for A2(t) in the model equations of the Supplemental text (see bottom of PDF) that led to the analytical solutions given in Eq. 7. Use of a constant value for A2(t) linearized the equation and thus permitted a solution. We also used a linear representation for g(x). Such linearization of the equations is warranted when length changes and velocities are small and myosin kinetics and its sensitivity to strain are constant. It is likely, for example, that the rate constants related to transitions from a force-producing state are not strictly linearly related to strain. We must keep in mind that our analytical solutions are useful to characterize myosin kinetics and the strain dependency of the detachment rate only to the extent that our model adequately reflects the underlying processes.
Conclusion
Our findings suggest that phases 2 and 3 of the typical step force response result from a transiently reduced myofilament force caused by a briefly enhanced crossbridge detachment rate with stretch. Furthermore, the elevated force of phase 4 does not necessarily reflect further activation of the thin filament by stretch, but rather a power-law viscoelastic response commonly found in biological tissues. If both these hypotheses are correct, then an enhanced rate of crossbridge detachment with stretch, possibly through a Pi-dependent mechanism, would result in the accelerated relaxation observed with stretch. This stretch-dependent detachment mechanism before MgADP release, if true, could play a significant role in underlying LV diastolic function and dysfunction.
Acknowledgments
Henk L. Granzier served as editor.
This research was supported by grants from the National Institutes of Health (R01 HL-118524, M.M. LeWinter; R01 HL-122744, M. Meyer), the National Institute of Arthritis and Musculoskeletal and Skin Diseases (R01-AR064274, D.M. Swank), the American Heart Association (17SDG33370153, B.C.W. Tanner), and the National Science Foundation (1660908, B.M. Palmer; 1656450, B.C.W. Tanner).
The authors declare no competing financial interests.
Author contributions: All authors participated in conceptualization of the overall topic and in editing the manuscript. B.M. Palmer designed experiments, wrote relevant software, analyzed data, and wrote the original draft. D.M. Swank, M.S. Miller, and M.M. LeWinter interpreted data, provided critical reviews, and curated key references. B.C.W. Tanner collected and curated raw data from mouse myocardium. M. Meyer and M.M. LeWinter provided funds and key resources including laboratory space and human myocardium. All authors approved the final version of the manuscript.