Multiciliated cells (MCCs) promote fluid flow through coordinated ciliary beating, which requires properly organized basal bodies (BBs). Airway MCCs have large numbers of BBs, which are uniformly oriented and, as we show here, align linearly. The mechanism for BB alignment is unexplored. To study this mechanism, we developed a long-term and high-resolution live-imaging system and used it to observe green fluorescent protein–centrin2–labeled BBs in cultured mouse tracheal MCCs. During MCC differentiation, the BB array adopted four stereotypical patterns, from a clustering “floret” pattern to the linear “alignment.” This alignment process was correlated with BB orientations, revealed by double immunostaining for BBs and their asymmetrically associated basal feet (BF). The BB alignment was disrupted by disturbing apical microtubules with nocodazole and by a BF-depleting Odf2 mutation. We constructed a theoretical model, which indicated that the apical cytoskeleton, acting like a viscoelastic fluid, provides a self-organizing mechanism in tracheal MCCs to align BBs linearly for mucociliary transport.
Introduction
The formation of mature epithelial sheets involves multiple steps in which epithelial cells adhere to each other to form a tight junction–based paracellular barrier, become polarized, and subsequently take on more specific differentiation states as they adopt the highly ordered structures required to elicit specific biological functions in vertebrates (Guillot and Lecuit, 2013; Rodriguez-Boulan and Macara, 2014; Tamura and Tsukita, 2014). How such complex processes are regulated is a fundamental question in cell biology and developmental biology.
Multiciliated cells (MCCs) are uniquely polarized to drive fluid transport in tissues by the synchronous beating and metachronal waves of hundreds of motile cilia on the apical membrane (Guirao and Joanny, 2007; Elgeti and Gompper, 2013). A differentiating MCC contains hundreds of basal bodies (BBs), which are short cylindrical structures at the base of mature cilia that are docked at the apical membrane (Anderson, 1972; Satir and Dirksen, 2011). In most types of MCCs, the orientation of the BBs, identified by their asymmetrically associated basal feet (BF), is precisely coordinated to support efficient mucociliary transport (Kunimoto et al., 2012; Chien et al., 2013).
The positional distribution of BBs (BB array) in the apical plane of MCCs depends on the cell type. For example, the BBs of ependymal MCCs in the brain exhibit unipolar clustering in the apical plane (Mirzadeh et al., 2010), whereas those of Xenopus laevis larval skin MCCs are evenly distributed throughout the entire apical region (Werner et al., 2011; Turk et al., 2015). Cytoskeletons are involved in regulating these systems, in which microtubules (MTs) are thought to synchronize BB orientation downstream of the planar cell polarity (PCP) core-protein functions (Vladar et al., 2012). Subapical actin is required for the proper distance between neighboring BBs (Werner et al., 2011), and myosin II activity plays a role in the unipolar migration of BB clusters (Hirota et al., 2010). However, the mechanisms involved in correctly assembling and maintaining the proper distribution of BBs on the cell surface remain to be fully elucidated.
In the present study, we examined mouse tracheal MCCs in which the BBs are linearly aligned, a pattern also found in oviduct MCCs. This striking pattern prompted us to address the mechanism by which these BBs become regularly aligned beneath the apical membrane. To follow BB pattern formation during MCC maturation, we developed a novel long-term and high-resolution live-imaging system in which cultured tracheal MCCs could be maintained as constantly moving specimens with beating cilia. We found that the development of the BB alignment pattern is highly dynamic and is achieved through a characteristic process, which we classified into four stereotypical patterns of BB array: “floret,” “scatter,” “partial alignment,” and “alignment.” Perturbing apical MTs caused the linear BB alignment pattern to revert to a floret-like pattern, and a genetic loss of BF that decreased MT density led to a failure to achieve BB alignment. Finally, we constructed a mathematical model for BB alignment based on an active hydrodynamic theory. This model showed the ability of cytoskeletal systems to self-organize BBs into specific patterns.
Results
The BB array adopts four stereotypical patterns during MCC differentiation, as revealed by long-term live imaging
In an individual MCC, BBs are generated via centrosome and deuterosome pathways and dock to the apical membrane to generate cilia (Stubbs et al., 2012; Zhao et al., 2013; Al Jord et al., 2014). When we examined the MCCs of adult mouse trachea and oviduct (Fig. S1 A), we found a strikingly linear BB alignment that was similar to the MCCs of cultured mouse tracheal epithelial cells (MTECs) prepared from the GFP-centrin2 transgenic mouse trachea (Fig. 1, A and B). To study the mechanism involved in BB alignment in the apical plane of MCCs, we developed a live imaging system that can be used for long periods (see Materials and methods for details). Using this system, we observed live GFP-centrin2–expressing MTECs (Higginbotham et al., 2004; Fig. 1, C–E) for 5–6 d, during which the differentiation of MCCs with beating cilia was unaffected (Fig. S1, E–H; and Video 1) and specimens in constant motion could be imaged.
Live imaging revealed that BBs first appeared as clusters with short cilia localized to the apical membrane (Fig. S1 B), which we termed the floret pattern. Subsequently, we found that BB florets scattered over the apical cell plane (scatter pattern) and neither clustered nor formed regular alignments. Then, around day 2, three to five neighboring BBs appeared to align with each other in a side-by-side fashion to form short lines (partial alignment pattern). By day 4, these short BB lines appeared to coalesce to form longer, parallel lines (alignment pattern; Fig. 1 E and Video 2). To quantitatively characterize these postciliogenesis BB arrays, we introduced an index of alignment (Ia), which has a high value when the BBs in a single cell are aligned (Fig. S1, C and D). Using Ia, we classified BB array patterns as follows: <0.22 (floret), 0.22–0.33 (scatter), 0.33–0.43 (partial alignment), and >0.43 (alignment; Fig. 1 F).
We next tracked the spatiotemporal dynamics of individual BBs by imaging GFP-centrin2. BBs in the floret pattern moved in and out of the area of the originally assigned floret cluster, and as a result, sets of BBs that later formed a line did not originate from a single floret (Fig. 2 A and Video 3). Over the course of MCC culture, the Ia value revealed a long-term ascending trend (Fig. 2 B), with a nearly constant number of BBs (Fig. 2 C). We found that the BBs moved most rapidly when they transitioned from the floret to the scatter pattern and then gradually slowed as they approached the alignment configuration (Fig. 2 D, left). After BB alignment was established, only minor changes occurred. We also observed occasional intermittent bursts of BB velocity caused by the large cellular deformation caused by the cell’s reconnection with a neighboring cell (Fig. 2 D, right). Collectively, our live imaging system of MCCs with quantitative analyses revealed that the BB array adopted four stereotypical patterns, from a clustering floret pattern to a linear alignment during MCC differentiation.
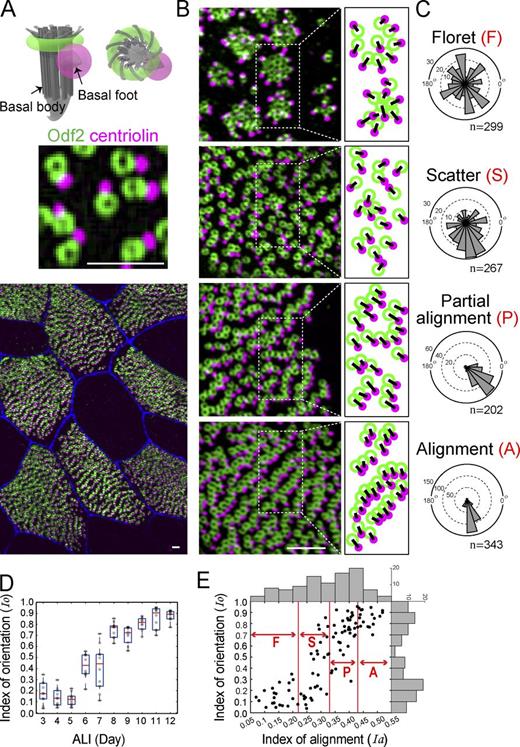
The establishment of BB alignment is correlated with the refinement of BB orientation
Although earlier studies (Guirao et al., 2010; Werner et al., 2011) showed that the interplay between BB position and orientation underlies proper ciliary beating in Xenopus embryonic skin and mouse brain, little is known about this process in tracheal MCCs. We examined the development of tracheal BB orientation in the course of cell maturation and its correlation with BB alignment. By immunostaining Odf2 (Nakagawa et al., 2001) and centriolin (Gromley et al., 2003), which mark the positions of BBs and BF, respectively (Fig. 3 A and Fig. S2 A), we determined the orientation of each BB (Fig. 3, B and C), and then estimated the degree of uniformity of BB orientation by introducing the index of orientation (Io) (see Fig. S2 B and Materials and methods for details). During the progressive refinement of the BB orientation over time, the Io exhibited a rapid increase around air–liquid interface (ALI) days 6–7. The Io values taken from all of the samples exhibit a bimodal distribution, in which a group of cells with low (<0.3) values transitioned into cells with high (>0.7) Io values within 2 d. In the mouse trachea, cilia-generated directional fluid flow is absent at birth. At postnatal day 5, it is initially acquired rapidly within 48 h and reaches a plateau at postnatal day 9 (Francis et al., 2009). Because the BB orientation indicates the beating direction of the cilia, the bimodal Io values may correspond to the timing of fluid flow acquisition observed in the trachea.
We also found a positive correlation between the alignment and orientation of BBs (Fig. 3 E). Specifically, Ia > 0.25 was coincident with the increase in Io. When Ia reached 0.4, Io was high (Io > 0.8). This relationship suggests a cooperative interaction between BB alignment and BB orientation. However, given that these analyses were based on fixed samples, the question remains whether BB alignment serves to facilitate the uniformity of BB orientations. Detailed investigations are needed to address the causal relationship between BB alignment and orientation.
The apical cytoskeletons in MCCs change during BB alignment
BBs were reported to be associated with the apical cytoskeleton (Gordon, 1982; Sandoz et al., 1988; Werner et al., 2011; Antoniades et al., 2014), which may play a key role in the BB array formation. We examined the distribution of the apical actin filaments, intermediate filaments (IFs), and MTs in MCCs presenting the four patterns of BB arrays. For this purpose, we used a combination of super-resolution fluorescence microscopy (Fig. S2, C and D; and Fig. S3 A) and ultra–high-voltage electron microscopic tomography (UHVEMT) on thick sections (Fig. 4 A and Videos 4, 5, 6, and 7), and serial thin-section electron microscopy (Fig. S3 B). The apical surface of MCCs turned out to contain a mixture of cytoskeletons (actin filaments, IFs, and MTs), which form a dense polymer network confined to a thin layer just underneath the apical membrane (Fig. S2, C and D; and Fig. S3 A).
Actin filaments were distributed between BBs (Fig. S2 C); these filaments are known to run mainly downward from microvilli interspersed between cilia (Chailley et al., 1989; Pan et al., 2007). They occasionally appeared to be associated with BBs and BF, consistent with previous studies (Reed et al., 1984; Kunimoto et al., 2012) and with our electron microscopic observation of heavy meromyosin (HMM)–treated samples (Fig. 4 B). We found that IFs, which were not decorated with HMM (a standard method for distinguishing them from actin filaments), were present between BBs, surrounding them at distances of ∼50–100 nm (Fig. S2 E). Closer examination of the early-stage BB pattern revealed that thick bundles of IFs frequently appeared around the BB florets; this pattern was not reported previously (Fig. 4 A).
The number and distribution of MTs increased during the progressive reorganization of BB alignment. The MT density around BBs increased during the transition from the floret to scatter pattern (Figs. 4 A and S3 A). In the floret pattern, only a few MTs associated with BF in the apical cortical region of MCCs. In the scatter, partial alignment, and alignment patterns, significant numbers of MTs, distributed nearly in parallel to the apical membrane, were associated with BF (Figs. 4 A and S3 B). During the transition toward the alignment pattern, increasing numbers of MTs appeared to form parallel bundles through mutual interactions (Figs. 4 A and S3 C). Thus, in the apical cortical layer containing the BBs, cytoskeletal structures were densely distributed, with some of them mutually interacting with BBs. Among these structures, the MTs were prominently aligned to promote BB alignment.
Actin and MT depolymerization affects BB alignment
To explore the role of the cytoskeleton in BB alignment, we treated MTECs with the actin depolymerizing agent cytochalasin D. We found that the alignment of BBs was disturbed and the spacing between BBs was decreased (Fig. S4 A), as well as dissociation of BBs from the apical membrane (Fig. S4 B). These observations are consistent with previous findings that actin plays an organizing role in BB spacing and apical docking (Pan et al., 2007; Werner et al., 2011; Antoniades et al., 2014). In addition, we noticed that cytochalasin D at a concentration that effectively disrupted the apical actin network, induced a shrinkage of the apical surface area in MCCs (Fig. S4 C) without significantly affecting the BB number (Fig. S4 D), resulting in a narrowing of the spacing between BBs. This observation suggests that actin determines BB positioning in an alternative way, not only by making interconnections at the proper distance between the BBs (Werner et al., 2011) but also by regulating the total area of the apical cell surface. A role for actin in regulating the apical surface area of MCCs was reported previously (Sedzinski et al., 2016).
MT depolymerization with nocodazole showed distinct effects on BB arrays. In GFP-centrin2–expressing MCCs in which the BBs were already aligned, nocodazole disturbed the BB alignment, resulting in clusters of BBs resembling the floret pattern (Fig. 5 A). The clusters of BBs were retained under an extended duration of MT depolymerization. On the other hand, washing out nocodazole remarkably returned the nocodazole-induced floret-like pattern to the partial alignment pattern, suggesting that transitions between these states are reversible and MT dependent (Fig. 5, A and B; and Video 8). Furthermore, the response to nocodazole treatment differed depending on the state of BB alignment. The clusters of BBs were clearer on earlier-stage cells (Fig. 5 C), and the change in their Ia occurred more rapidly (Fig. 5 D). Because fewer MTs were associated with BBs in the floret pattern (Fig. 4 A), depolymerizing MTs in the earlier-stage cells would presumably lead to a more severe phenotype.
In nocodazole-treated cells, we confirmed that the immunofluorescent intensity of MTs was reduced (Fig. 5 E), whereas the actin filament distribution was relatively unaffected (Fig. S4 E). The networks of keratin IFs were profoundly altered by nocodazole, including the formation of filament bundles surrounding the floret-like BBs (Fig. 5, F and G). Similar morphological changes in IFs in response to shear stress have been reported in cultured human alveolar A549 epithelial cells (Flitney et al., 2009).
We also followed changes in BB orientation during nocodazole treatment using fluorescence of GFP-centrin2 and centriolin for BBs and BF, respectively (Fig. 5 H). We found that the coordination of the BB orientation was disturbed by MT perturbation, similar to the case in the floret pattern in BB arrays in the earliest phase of differentiation. Nocodazole washout restored the coordination of BB orientation.
Although these findings revealed that MTs play a critical role in the linear alignment of BB arrays from the floret to the partial alignment/alignment patterns, and in the simultaneous coordination of BB orientation, we could not exclude the participation of actin filaments and IFs in maintaining the proper BB arrays. The fact that MT disruption also affected the organization of keratin IFs suggests that the cytoskeletons interact with each other. To explore this possibility, we examined the localization of plectin, a major IF-based cross-linker protein that can facilitate physical interactions among MTs, IFs, and actin (Svitkina et al., 1996; Wiche et al., 2015). Although a previous study showed that the transcription level of plectin is up-regulated in the MCCs of MTECs (Hoh et al., 2012), the spatial distribution of plectin in the cells was not examined. We found that the distribution of plectin closely corresponded to that of keratin IFs (Fig. S5 A) and partly colocalized with MTs (Fig. S5 B). These findings support the idea that the three types of cytoskeletons associate with each other through cross-linkers like plectin and thus could act cooperatively to drive the dynamic motion of BBs.
Loss of BF from the BBs causes undirected BB movement and perturbs the establishment of the alignment pattern
Our previous work (Kunimoto et al., 2012) revealed the requirement of Odf2-based BF for functional mucociliary clearance. In the tracheal MCCs of Odf2 mutant (Odf2ΔEx6,7ΔEx6,7) mice, the absence of BF impaired the regularity of the BB arrays and the polarized organization of apical MTs. However, the dynamic process of the BB array development in these mutant mice was unknown. To resolve this issue, we next examined MTECs prepared from GFP-centrin2-transgenic Odf2 mutant mice generated in this study, in which the BBs lack BF.
We detected BBs in the typical floret pattern in the Odf2ΔEx6,7ΔEx6,7 GFP-centrin2 MTECs at the earliest stage of MCCs differentiation (Fig. 6 A and Video 8). Subsequently, and in sharp contrast to wild-type GFP-centrin2-MTECs (Figs. 1 E and 2 B), GFP-centrin2 in the BBs in Odf2ΔEx6,7ΔEx6,7MTECs revealed only a partial progression of the floret pattern to the scatter pattern and no progression to the partial alignment or alignment pattern. The dynamic behavior of the BBs was further specified by determining the Ias, which remained low in the Odf2ΔEx6,7ΔEx6,7 GFP-centrin2 MTECs (Fig. 6 B). In addition, tracheas from these mutant mice showed disorganized BB alignment (Fig. 6 C). These findings strongly suggest that BF-associated cytoskeletal structures, such as MTs, play important roles in BB alignment.
Mathematical modeling of the experimentally observed BB patterns
To obtain insight into the mechanisms underlying the BB patterns observed experimentally, we constructed a mathematical model for BB arrays based on the spatiotemporal dynamics of the apical cytoskeleton. The apical cytoskeleton is highly dynamic because of filament polymerization and depolymerization and because of the contractile stresses exerted by cytoskeletal motors such as myosin and kinesin. In addition, the cytoskeletal network behaves like a viscoelastic fluid (Jülicher et al., 2007) in the timescale relevant to multiciliated cell maturation (hours). Using this information, we developed a mathematical model for the formation of BB alignment based on active hydrodynamic theories describing the cytoskeleton (Marchetti et al., 2013; Prost et al., 2015). In our model, the apical cytoskeletons are treated as a two-dimensional viscous fluid that involves the activities of contractile force κc mediated by cytoskeletal motors, and filament polymerization with the rate κp. In this model, the BBs are regarded as objects that associate with the cytoskeletons by their BF (Kunimoto et al., 2012; Tateishi et al., 2013) and hence are transported by active cytoskeletal flows (Fig. 7 A and see Materials and methods) and are subject to random fluctuations in cytoskeletal motions.
Above a critical activity for a given κp, the contracting force leads to spontaneous pattern formation, classified as spot, stripe, and intermediate patterns (Fig. 7 B). As the BBs associated with cytoskeleton via their BF were transported by cytoskeletal flows, BBs that settled into the cytoskeletal system under stripe-forming conditions exhibited sequential transitions from the floret through scatter and partial alignment and, finally, alignment patterns (Fig. 7 C and Video 9). In the earliest stage, in which the cytoskeleton was dilute, the BBs failed to associate with the cytoskeleton and were not advected by the flow, leading them to scatter from the florets via random walk. In contrast, in later stages, abundant cytoskeletal elements gave rise to spontaneous flows to form stripe arrays and hence to organize the BBs into alignment. These results correlated well with our experimental results of the characteristic patterning of BB arrays, which reached BB alignment through the four stereotypical patterns (Fig. 1, E and F).
The model also explained the cellular responses to perturbations observed in our experiments. Changing the model parameters to a lower polymerization rate and higher viscosity resulted in BB cluster formation (Fig. 7 D and Video 10), reminiscent of the nocodazole-induced clustering of BBs (Fig. 5 A). Our model analysis indicated that this clustering was attributed to two main events: (1) the lower polymerization rate shifted the cytoskeletal pattern from stripes to spots (Fig. 7 B); and (2) IFs were bundled after nocodazole treatment (Fig. 5, F and G), which stiffened the apical cytoskeletons and effectively increased their viscosity, resulting in slower and long-range flow (Mayer et al., 2010) that gathered many BBs to a large spot. At even lower polymerization rates (Fig. 7 E), the cytoskeleton no longer developed into any pattern and, accordingly, the BBs exhibited only the transition from floret to scatter via random fluctuations. This pattern was similar to the phenotype of Odf2 mutant cells, in which the apical MTs were not abundant (Kunimoto et al., 2012) and the BBs transitioned from floret to scatter but failed to develop into alignment (Fig. 6 A and Video 10). This model simulation explained our observations that nocodazole treatment and the genetic loss of BF perturbed the apical MTs to disturb the normal patterns of BB distribution and behavior.
Next, using this model, we examined how the conditions of the cytoskeleton at the cell boundary (the region in contact with a neighboring cell) affect the BB patterns within a single cell. This examination of boundary conditions was motivated by the observation that PCP molecules induce an asymmetric MT distribution at the cell membrane (Vladar et al., 2012; Shi et al., 2016) and that this biased distribution of MTs can guide BB alignment in a certain direction. To investigate how cytoskeletons along a boundary control BB patterns, we performed simulations in which the cytoskeletal velocity at the cell boundaries remained static (nonslip), which was based on our observation that the BBs move slowly at cell boundaries, and the cytoskeleton concentration was set as asymmetric along the long axis of a cell at an early stage of the simulation. The results shown in Fig. S5 C demonstrated that modifying the boundary conditions allowed for the precise control of the direction of BB lines in a direction perpendicular to the long axis of the cell. This model prediction is consistent with our experimental observations that an asymmetric MT distribution was established around the Floret stage (Fig. S5 D) and that the parallel BB alignments in a single cell were perpendicular to the long axis of the cell (Fig. S5 E).
Discussion
In the present study, we found that BB alignment in mature trachea and MTECs occurred through stereotypical changes in the BB array and that a self-organization mechanism involving the associated apical cytoskeleton could give rise to these patterns. The distribution patterns of BBs determined the positions of beating cilia, the biological significance of which has been widely studied in the context of synchronization and metachronality in the ciliary beating pattern (Werner et al., 2011; Brooks and Wallingford, 2014). Recent theoretical studies indicated that the pattern of ciliary positions affects the onset (Guirao and Joanny, 2007) and the efficiency of fluid transport (Osterman and Vilfan, 2011; Elgeti and Gompper, 2013) through the coordination of synchronized or metachronal ciliary beating. On the other hand, very few studies have addressed the physical mechanism underlying the establishment of the cilia positioning itself. Previous studies in Xenopus (Werner et al., 2011) and mouse brain (Boutin et al., 2014) demonstrated that the cytoskeleton is a common key player responsible for the formation and regulation of ciliary distribution, despite differences in the ciliary patterns of various cell types.
Here, we quantified the dynamic, sequential changes in ciliary patterns, which we termed floret, scatter, partial alignment, and alignment, that occurred during the maturation of mouse tracheal MCCs. Furthermore, we demonstrated that interactions between components of the apical cytoskeleton and BBs were crucial for establishing and maintaining these ciliary patterns; the genetic loss of BF in Odf2ΔEx6,7ΔEx6,7 MTECs prevented BBs from achieving the alignment pattern, and drug-induced apical MT disruption caused the alignment pattern to change to a floret-like pattern. These changes in BB patterns were positively correlated with the refinement of ciliary orientation, indicating that ciliary alignment may have stabilized the unidirectionality of the BBs, to enhance the function of MCCs. The effects of other factors, such as cytoskeletal polarity (Shimada et al., 2006; Vladar et al., 2012), regulation by PCP signaling (Seifert and Mlodzik, 2007; Park et al., 2008; Mitchell et al., 2009; Boutin et al., 2014), and hydrodynamic coupling between cilia (Mitchell et al., 2007; Guirao et al., 2010; Matsuo et al., 2013) need to be examined in future studies.
Using our findings, we constructed a theoretical model for BB patterning driven by active reorganization of the apical cytoskeleton. This model reproduced the most prominent aspects of BB dynamics identified in our imaging analyses, including their spontaneous alignment during the normal development of MCCs in MTECs, their temporal clustering induced by nocodazole treatment, and their disordered pattern in the Odf2ΔEx6,7ΔEx6,7 MTECs. Our model study also suggested that there is a joint effect between PCP regulation and cytoskeletal self-organization during the establishment of BB alignment. In terms of our simulation, PCPs define the boundary conditions of the system, which determine the directionality of the cytoskeletal pattern and BB alignment. These results provide mechanistic insight into the possible role of the cytoskeleton in establishing large-scale linear BB arrays in a cell sheet. Together, our experimental and theoretical studies highlight a possible biological function of the apical cytoskeleton in tracheal MCCs in the linear alignment of cilia, as a typical example of the terminal differentiation of epithelial cell sheets.
Self-organized cytoskeletal patterns are relevant in many biological functions, such as spindle body formation, in which motor-mediated interactions between MTs determine the viscoelastic nature of the spindle (Shimamoto et al., 2011; Brugués and Needleman, 2014). Self-organized cytoskeletal mechanisms are also suggested to be involved in apical structure formation (Chaudhuri et al., 2011; Gowrishankar et al., 2012). The model of BB alignment and the apical cytoskeleton in tracheal MCCs set forth here was based on the apical cytoskeleton as a dynamic material with cytoskeleton-dependent viscosity. Although different BB distributions in the apical layer have been reported in various organ systems, some common mechanisms may be involved in the formation and regulation of BB organization. Our present study provides a new framework for understanding apical cytoskeletal function as exemplified in multiciliated epithelial cells. Such an autonomous, self-organizing mechanism with or without a coupled cell signaling system may play critical roles in various morphogenetic processes in both single-cell and multicellular systems.
Materials and methods
Animals
All procedures involving animals were approved by the institutional animal care and use committee of Osaka University. The mice used in this study included GFP-centrin2 (Higginbotham et al., 2004), wild-type C57BL/6J (CLEA Japan), and Odf2ΔEx6,7ΔEx6,7 GFP-centrin2. To generate Odf2ΔEx6,7ΔEx6,7 GFP-centrin2 mice, homozygous GFP-centrin2 mice were crossed with Odf2flox/+ mice to produce male Odf2flox/+ GFP-centrin2 mice. Then, the latter were intercrossed with female CAGCre/+; Odf2flox-del/+ mice to generate Odf2ΔEx6,7ΔEx6,7 GFP-centrin2 mice. The protocols for genotyping were described previously (Kunimoto et al., 2012).
Primary culture of tracheal cells and long-term live imaging
MTEC cultures were prepared from the trachea of mice at 7–10 wk of age as described previously (You et al., 2002), with replacement of the conventional medium. To improve the cell yield, enzymatic digestion was performed with gentle shaking at 4°C for 16–20 h. This method routinely yielded ∼1.08 × 106 cells/ml from four mice, which was sufficient for 20 transwell 24-well filters (Corning). The enzymatic digestion was stopped by adding FBS (Cell Culture Bioscience) to the cell suspension at a final concentration of 10%. Cells were pooled by centrifugation at 400 g for 10 min at 4°C, then resuspended in MTEC Basic Medium (You et al., 2002) with 10% FBS for 3.5 h at 37°C, 5% CO2 to adhere contaminating fibroblasts. Nonadherent cells were then collected by centrifugation, counted, and seeded at 105 cells/cm2 onto polyester transwell filters (Corning) coated with 50 µg/ml collagen type I (Corning). The proliferation stage was maintained using the commercially available BEGM BulletKit (CC-3170; Lonza). The ALI stage was created after 4 d of culture using PneumaCult (05001; STEMCELL Technologies) according to the manufacturer’s instructions. For live imaging, transwell filters with a MTEC sheet (ALI 5–6 d) were cut out from the plastic support and inverted (cell side facing down) onto a glass-bottomed dish (D11140H; Matsunami Glass). Medium was supplied from an additional chamber attached to the back surface of the inverted insert. The medium was changed every other day.
Inhibitor experiments and HMM treatment
Inhibitor experiments were performed either during live imaging or under normal incubation conditions. For MT depolymerization, 6.6 µM nocodazole (Sigma-Aldrich) was applied to MTECs at ALI 6 d for 2 h, then replaced with 500 µl of fresh medium for recovery. For actin depolymerization, 10 µM cytochalasin D (Sigma-Aldrich) was used at ALI 7 d for 5–10 h.
To permit HMM to diffuse into the cells, MTECs at ALI 28 d were incubated with 0.1% Triton X-100/0.01 µM paclitaxel in PHEM buffer (60 mM Pipes, pH 6.9, 25 mM Hepes, pH 6.9, 10 mM EGTA, and 2 mM MgCl2) for 15 min, then washed with PHEM buffer. Freshly thawed rabbit HMM solution was dialyzed against PHEM buffer at a final concentration of 1 mg/ml. The cells were then incubated with this HMM solution and 0.01 µM paclitaxel for 1 h at RT, washed, and fixed for thin-section electron microscopy.
Indirect immunofluorescence
MTECs and whole-mount trachea and oviduct were fixed in cold methanol (−20°C) or 4% PFA in Hepes-buffered saline (RT), permeabilized with 0.2% Triton X-100/PBS for 5 min (RT), and then incubated in 1% BSA/PBS for 30 min (RT). Incubations with primary and secondary antibodies were performed for 1 h each (RT). The following primary antibodies were used: rabbit anti-Odf2/Cenexin (1:500; Abcam), mouse anti–α-tubulin (1:500; Sigma-Aldrich), rabbit anti-Vangl1 (1:500; Sigma-Aldrich), rabbit anti–ZO-1 (1:500; Invitrogen), rat anti-Odf2 (Tateishi et al., 2013), rat anti–centriolin (Ishikawa et al., 2005), mouse anti–ZO-1 (T8-754; Kitajiri et al., 2004), rabbit anti–plectin 1 (1:100; Abcam), and mouse anti–keratin 8 (provided by A. Hirako and K. Owaribe, Nagoya University, Nagoya, Japan) antibodies. Secondary antibodies (1:500) included rat anti-GFP (Invitrogen) and species-specific Alexa Fluor 488, 568, and 647 (Invitrogen) antibodies. Rhodamin-conjugated phalloidin was purchased from Invitrogen.
Microscopy
Live imaging and confocal microscopy
BB movement was recorded using a Spinning Disk-Olympus super-resolution microscope (SD-OSR; Olympus; Hayashi and Okada, 2015) equipped with a silicon oil-immersion objective lens (UPlanSApo 60× Sil, NA 1.3; Olympus), a sCMOS camera (ORCA-Flash 4.0 v2; Hamamatsu Photonics), appropriate filter sets for DAPI/FITC/TRITC, a motorized scanning deck, and an incubation chamber (37°C; 5% CO2; 85% humidity; Tokai Hit). The recording was performed by multistage acquisitions with 10–30 fields of view, each covering ∼10 cells/field. Time intervals were 30 min for long-term recording, 15 min under nocodazole treatment, and 1–2 h under cytochalasin D treatment. Image acquisition was set to z-series of 8–12 planes with a 0.5-µm distance. Immunofluorescently stained samples were imaged using a silicon oil-immersion objective lens (UPlanSApo 60× Sil, NA 1.3; Olympus) and 1.6× conversion lens. All hardware was controlled with MetaMorph (Molecular Devices). The resulting 3D images were converted into 2D images by maximum intensity projection in the z-direction before the image analysis necessary for detecting BBs and BF.
Thin-section electron microscopy and electron tomography with UHVEMT
MTECs were fixed with 2.5% glutaraldehyde and 2% PFA at 37°C for 1 h. The following steps were based on classical methods for sample preparation for electron microscopy (Ishikawa et al., 1969). Serial sections of 90 nm were cut on an ultramicrotome (Ultracut E; Leica Biosystems) and stained with uranyl acetate and lead citrate for double contrasting. Image observation was performed using a JEM 1400-Plus (JEOL). For observation using UHVEM Tomography, 700-nm-thick section specimens were observed using an ultra–high-voltage electron microscope operating at 1 MeV (H-3000; Hitachi). The images were acquired at 25,000 times from −60° to +60° at 2° intervals around a single-axis tilt series, as described previously (Kunimoto et al., 2012).
Cilia beating
Cilia beating was recorded using a high-speed camera (FASTCAM MC2.1; Photron) connected to an upright microscope (Axioplan; ZEISS) with 63× objectives.
Image analysis
Index of alignment Ia
To quantify the degree of alignment in BB configurations, we constructed the index of alignment Ia (Fig. S1 D). Ia is calculated from the given positions of BBs in a single cell, ri(i = 1, ..., N), by the following three steps.
Step 1: Determination of neighboring BBs
BBs whose positions were within a range of 1.3d from ri were determined to be neighbors of the ith BB. Here, d represents the diameter of the BBs, and we set d = 4 pixels. Note that the distance from a BB to its second-nearest BBs in a square lattice is , and our choice of 1.3d allows us to exclude the second-nearest BBs from the neighboring BBs of a given BB.
Step 2: Local evaluation of the alignment
For every ith BB with n neighbors, the local index of alignment, Ia,i, was evaluated using the following set of equations:
where is the acute including angle between the vector rj − ri and rk − ri. The linearity function L has high values (∼1) for only linearly aligned BBs and acts as a filter to distinguish aligned patterns from other configurations. The weight function w was used to increase the effect of the closer BBs within the neighborhood.
If n ≥ 4, then we set Ia,i = 0. If n = 1, we performed the following process. Let j be the label of the single neighboring BB of the ith BB. If the jth BB has two neighboring BBs, then we define Ia,i = Ia,j, by which the BBs at the edge of the line have a high value. If the number of neighbors of the jth BB is 1 or more than 3, we define Ia,i = 0.
Ia,i is bounded in the interval [0, 1] with 1 indicating highly aligned patterns of BBs and 0 indicating nonlinear configurations.
Step 3: Averaging
Finally, the index of alignment Ia was defined as the mean of Ia,is of the BBs within a single cell:
Index of orientation Io
To measure the variation in basal foot orientations within a single cell, we introduced the index of orientation Io (Fig. S3 B). Io is calculated as follows. Suppose we have a set of vectors, each of which originates from the center of a BB and ends at its accompanying BF. We denote the angle between each vector and the horizontal axis by θi(i = 1, ..., N), where N represents the total number of BBs within a single cell. The θis were first transformed into unit vectors in two-dimensional pis by
After this transformation, a single mean vector p was computed by
The index of orientation Io is defined as . Note that Io is bounded in the interval [0, 1]. Io is an indicator of the spread of BF orientations, θi. If all BF point in the same direction, Io will be 1. If the BF orientations are random, Io will be 0.
For comparison, Fig. S3 B shows the Io values calculated for five representative angle datasets illustrated by rose diagrams, which are commonly used to represent BF orientations (Chien et al., 2013).
Mathematical model of BB alignment
Hydrodynamic description of the apical cytoskeleton
In short timescales (seconds), the cytoskeleton behaves like an elastic solid, but in the longer timescales relevant to BB alignment (hours), it acts like a viscous fluid because of the polymerization/depolymerization and motor-induced dynamic remodeling of cytoskeletal filaments. Several theoretical studies modeling the cytoskeleton as an active viscous fluid have been successfully applied to a wide range of biological systems, including muscle sarcomeres (Banerjee and Marchetti, 2011), moving cells (Shao et al., 2012), the contractile ring (Salbreux et al., 2009), the cell cortex (Rauzi et al., 2010), and the metaphase spindle (Brugués and Needleman, 2014). In the following analysis, we based our mathematical model on the description of the apical cytoskeleton as an active fluid.
Because the apical surface is very thin compared with the other dimensions of the whole cell, we restricted our model to two dimensions. We described the apical cytoskeleton dynamics using two continuum fields: fluid velocity v(x,t) and cytoskeleton concentration C(x,t), where x(x,y) represents the apical xy-plane coordinates and t is the time. We did not distinguish between the components of the apical cytoskeleton, i.e., actin filaments, IFs, and MTs. This assumption was supported by our experimental observations of plectin localization (Figs. S5, A and B), which suggested that complex interactions occur among the apical cytoskeletons during the progression of BB alignment and that these interactions cause the different cytoskeletons to have cooperative dynamics, behaving like a single fluid entity on a long timescale. In general, filament orientation is thought to play an important role in cytoskeletal pattern formations (Marchetti et al., 2013), and the concentration C(x,t) alone does not describe all of the properties of the cytoskeleton. In this study, however, the minimal model in which the apical cytoskeleton is described by the concentration C(x,t) and velocity v(x,t) was able to capture the most prominent aspects of BB dynamics, including the aggregation induced by nocodazole treatment, the disordered patterns in Odf2 mutant cells, and the spontaneous alignment during normal development.
Because of the low Reynolds number at the cellular length scale, the fluid acceleration is negligible compared with viscosity. Under this condition, the force balance equation is given by
The left-hand side of Eq. 1 is the force acting on the fluid, whereas the right-hand side represents the friction between the cytoskeletal network and the penetrating cytosol. Although the friction coefficient γ depends on the microscopic environment between the cytoskeleton and cytosol, we treat γ as a constant. The stress tensor, σ, is composed of passive and active parts as
The passive contribution is given by
where η and λ are shear and bulk viscosities arising from internal friction in the cytoskeleton, d(= 2) is the space dimension, and I is the unit tensor. The active contribution, σa, originates from the contractile forces exerted by molecular motors, like kinesin and myosin, bound to the cytoskeleton. We chose σa as a simple isotropic contraction:
Here, m is the concentration of motors bound to the cytoskeleton. Provided that the motor diffuses sufficiently rapidly, the motor concentration is assumed to be uniform. σa describes the change in chemical potential because of the hydrolysis of ATP by a motor, and F(C) is the duty ratio of motors and is given by
where kon and koff are, respectively, the binding and unbinding rates according to first-order reaction kinetics.
To complete the continuum description, we need equations describing the dynamics of the cytoskeleton concentration C. Because C obeys the conservation law with concentration flow j and reaction R(C), we obtain
The form of the concentration flow j is
The first term in the right-hand side of Eq. 7 is the flow arising from advection by the fluid. The second term represents the diffusive flow with diffusion coefficient D. The reaction term R(C) consists of polymerization and depolymerization processes:
where kp and kd are, respectively, the polymerization and depolymerization rates of the cytoskeleton. Eqs. 1–8 lead to the final form of the equations describing the apical cytoskeleton as
and
where kc = m · μ is the effective contraction strength and is the saturation concentration.
Dynamics of the BB
Based on a previous study (Kunimoto et al., 2012) showing that the BF associate with apical MTs, we modeled BBs as hard “particles” that associate with the apical cytoskeleton via their accompanying BF and hence are advected by the cytoskeletal flow. For simplicity, we assumed that each BB is a circular object with radius r and that the motion of the BBs does not affect the cytoskeleton and is completely determined by the cytoskeletal fluid velocity v. The steric interaction that prevents BBs from merging can be modeled by using a repulsive force acting on overlapping BBs as:
where Xi represents the position of the ith BB and ks is the strength of the steric interaction. To prevent the penetration of cytoskeleton into the BBs, we consider another repulsive force acting between the cytoskeleton and BBs, of the form where is the spatial mean of the concentration gradient inside the ith BB. Our experimental data showing that not all BF associate with MTs suggest that the interaction between the cytoskeleton and each BF is stochastic. To take this effect into account, a random variable ξ following a normal distribution is added to the flow-advected motion of the BBs. The statistics of ξ can be written as ξ(t) = 0 and , where the angle brackets denote an ensemble mean, and δ is the delta function. A represents the amplitude of fluctuation.
To summarize, the time evolution of the position of the ith BB Xi is described by
where is the spatial mean fluid velocity inside the ith BB.
Nondimensionalized form model equations
To obtain a set of core parameters, we nondimensionalize the model equations as
and
by introducing the following scale transformations:
and dimensionless parameters
The variables and parameters of the model are summarized in Table 1.
Detection of BBs and BF
We used least-squares fitting to identify the positions of the BBs and BF in the immunofluorescence images. The fitting algorithm proceeded as follows.
Step 1
The fluorescence image of the BBs (BF) was normalized to scale the intensity between 0 and 1, and the fitting-error function E was calculated by
where W, I, and It are, respectively, the weight function, the normalized fluorescent image of the BBs (BF), and the target image. m and n are pixel indices. mc and nc represent the centers of the BBs (BF), which will be identified in step 2. The summation in Eq. 12 runs over the image I. W and It were specified as
where a, b, H, σb, and σf are the parameters characterizing the shape of a BB (BF). In the present study, we set a = 5 (pixel), b = 1 (pixel), H = 0.75, σb = 2 (pixel), and σf = 2 (pixel).
Step 2
Because E takes local minima at the positions of the BBs (BF), one can find the most likely positions of the BBs (BF) by detecting all of the minima of E. For this purpose, the right-hand side of Eqn. (S1) was rearranged using two-dimensional discrete convolution to obtain
where
represents the two-dimensional discrete convolution. Using Eq. 13, all of the pixel indices (mc, nc) whose values of E(mc, nc) were lower than a threshold value E* and smaller than those of their 8 nearest neighbors were extracted to identify all of the minima of E, i.e., the positions of the BBs (BF). We set E* = 5.
Step 3
All false-positive and false-negative detections were manually corrected.
BB–BF pairing algorithm
In the analysis of immunofluorescence images, individual BF needed to be correctly paired with their host BBs. To accomplish this, we applied a nearest-neighbor-pairing method, because each BF can be regarded as the nearest object of its host BB. The method we used was originally introduced by Labonté (1999) and improved later by Ohmi (2008).
The method is implemented in an iterative manner, as described in the following steps:
Step 1
Let ri(i = 1, ..., N) and qj(j = 1, ..., M) respectively be the two-dimensional coordinate vectors of the ith BB and the jth BF within a single cell. N(M) is the total number of BBs (BF). First, the weight vector αi was assigned to ri and βj was assigned to qj, and they were initialized as
where the superscript [·] indicates the iteration number.
Step 2
Next, the weight vector αi was subjected to the following change:
where cj denotes the index of the BB whose weight vector was closest to , and was given by
where the parameters and were initialized with given values as and , and then they were updated in the next step 3 (Eq. 14).
Similar to αi, the weight vector βj was updated by
where ci represents the index of the BF whose weight vector was closest to , and was given by
Step 3
Finally, and were updated via
Step 2 and Step 3 were alternatively repeated until ρ reached a given critical value of ρc. After completion of the cycles, if the distance between αi and βj was less than a certain critical value of , then we regarded the jth BF to be accompanying the ith BB. The algorithm described by steps 1–3 ensures a one-to-one correspondence between the BBs and BF.
In the present study, we used the following parameters: (pixel), (pixel), (pixel), , and (pixel).
BB tracking algorithm
To construct the trajectories of individual BBs, we needed to establish a correspondence between the BBs of different frames over time. To remove the effect of stage/sample drift on BB trajectories, the BB positions at each frame were translationally moved so that those centroid would be located at the spatial origin. Let I1 and I1 be two successive frames containing N1 and N2 BBs, respectively. The tracking technique used in the present study is based on two assumptions of BB motion: (1) BBs move from one frame to the next with small displacements, and (2) BBs within a correlation length move with similar speed. The displacements were calculated using pairwise distances Dij between the ith (i = 1, ..., N1) BB in one frame and the jth (i = 1, ..., N2) BB in the other. In contrast, similarity Sij is evaluated by
where m and n are pixel indices, represents the position of the i(j)th BB in the image , L is the correlation length, and indicates the mean intensity within an L × L window centered at in .
To establish the correspondence between BBs, we used the algorithm previously proposed by Scott and Longuet-Higgins (1991). The algorithm consists of three steps.
Step 1
The first step is to calculate a matrix named the proximity matrix Mij:
where is a characteristic length of BB displacements between subsequent images and represents a characteristic similarity of the motion pattern of neighboring BBs. In the present study, we set (pixel) and .
Step 2
The next step is to find the singular value decomposition of the matrix M such that M = UΣV, U and V are orthogonal matrices and Σ is the diagonal matrix.
Step 3
The final step is to replace all the entries of Σ by ones, resulting in the pairing matrix P: P = UIV, where I is the identity matrix. Each entry of is the measure of correspondence between the ith BB in one frame and the jth BB in the other. If an entry of is the maximum value of both the row i and the column j, then the ith BB is considered to correspond to the jth BB. The orthogonality of P ensures a one-to-one correspondence between the BBs in different frames.
Estimation of the amount of MTs around BBs from immunofluorescence images
Our method for estimating the amount of apical MTs has some limitations. First, MTs at the apical layer of MCCs are interspersed with hundreds of BBs. Considering that the barrel-shaped BB consists of nine triplets of MTs (Anderson, 1972; Tateishi et al., 2013), we cannot exclude the possibility that the visualized apical MTs were mixed with artifactual signals from the BB structure. Second, the decoration of MTs with anti–tubulin antibodies hinders the visualization of individual MTs, which typically overlapped with each other in the late stage of BB alignment (Fig. 4 A in the alignment pattern). Thus, the actual distribution of overlapping MTs may be underestimated. Our method presents an approximate comparison of the MTs covering the surface of MCCs at different stages rather than the actual number of apical MTs.
Method
The algorithm to estimate the amount of MTs around BBs in a single cell has four steps: (1) extraction of the cell boundary; (2) determination of the most in-focus z-plane of BBs; (3) detection of MTs; and (4) calculation of the surface coverage of MTs.
Step 1: Extraction of the cell boundary
The boundary of a single cell at each z-slice was extracted by manually tracing the line of the Vangl1 fluorescence signal located at the cell periphery.
Step 2: Determination of the most in-focus z-plane of BBs
The most in-focus z-plane of the BBs in a single cell, symbolized as zBB, was determined as the z-slice where the standard deviation of the fluorescence signal of Odf2 within a single cell reached its maximum value among all the z-slices.
Step 3: Detection of MTs
To detect MTs, each z-slice of the fluorescence image I(x,y) of the MTs was processed by a filter that removes background noise and enhances fibrous structures. For this purpose, we used a Frangi filter (Frangi et al., 1998), which is processed as follows. Given image I(x,y), a Hessian matrix of the image is first computed:
where is the convolution between I(x,y) and . denotes the Gaussian kernel with mean 0 and standard deviation σ, which corresponds to the width of MTs to be detected. Next, two eigenvalues of were computed , and the likelihood measurement of MTs was calculated as
where and . The terms containing and filter out spurious signals from blob-like structures and noise. In the present study, we set . Considering that the MTs to be detected are of different widths, σ is determined by maximizing the final likelihood of the MTs as
The range is set (pixel). The result of the Frangi filter L(x,y) is a probability map of the pixels being MTs at each z-slice.
Step 4: Calculation of the surface coverage of MTs
As the aforementioned probability depends on the fluorescence intensity of the original image I, a simple averaging of this probability over the area within a single cell would not give a value that can be used to compare the amount of MTs in cells at different stages. Thus, we performed a further binarization of the probability map to change L(x,y) into the surface coverage of MTs, which is a more robust quantity for comparing the amount of MTs. This binarization was performed at each z-slice. To ensure the reliability of our analysis, we examined a different threshold for the binarization that was computed using n-fold of the mean of the values of L(x,y) within a single cell (n = 0.5 to ∼1.0). We verified that the results of our analysis did not qualitatively change as long as n ranged from 0.5 to 1.0. The pixels with a value larger (or smaller) than the threshold were treated as MTs (or background) and assigned a value of 1 (or 0). Considering that the fluorescence signal of Odf2 comes from the z-position, which is slightly higher than the BB plane (Fig. 3 A), the surface coverage of MTs around BBs was calculated by averaging the values of the binarized maps over two z-slices located at z = zBB − 2Δz and zBB − 3Δz, where Δz(= 150 nm) represents the distance between neighboring z-slices. This choice of z-slices enabled us to effectively remove signals from cilia.
Measurement of the apical surface area
To measure the apical surface area of MCCs, the cell boundaries in an MTEC sheet were stained with antibodies against ZO-1. The apical surface area of a single MCC was determined as the area confined by ZO-1 and measured using IMAGEJ software (National Institutes of Health).
Notes for the mathematical model
1. Linear stability analysis
To investigate how the model described in the Materials and methods allowed for spatially inhomogeneous patterns, we performed a linear stability analysis. The model Eqs. 9 and 10 have a steady-state solution: To this solution, we add small perturbations of the form , where ω is the linear growth rate, is the wave vector, and and Δc are amplitudes of the spatial perturbation. Inserting into Eqs. 9 and 10 and retaining the first-order terms of Δu and Δc yields the following linear equations:
where . The condition of det(M) = 0 yields the dispersion relation:
has a peak at the positive wave number
and the spatial pattern with the wavenumber dominantly grows, and hence, spontaneous pattern formation occurs if the following condition is satisfied (Fig. 7 B):
2. Numerical scheme
The nondimensionalized model Eqs. 9–11 defined on a rectangular domain are discretized on a square grid with spacings h = 0.1 by the second-order finite difference scheme. In Fig. 7 (C–E), the system size is and the periodic conditions are assigned to the boundary values of c and u for approximating a large system. On the other hand, to examine the boundary effects, the system size in Fig. S5 C is set as and no-slip boundary conditions are assigned to u throughout the simulation. The boundary conditions of c in Fig. S5 C remain no-flux (j = 0) during and are changed to during , where is a fixed value. Note that hard walls are set at the system boundaries to confine the BBs within the system domain. For a given profile of c, Eq. 9 is solved by the Gauss–Seidel method (Press et al., 2007) to update u. Once u is known, to update c, Eq. 10 is numerically integrated with time steps , using the Lax–Wendroff method (Press et al., 2007), which is accurate up to the second order in time. We repeat this set of updates until the end of the simulation. Eq. 11 is integrated by the second order Adams–Bashforth method (Press et al., 2007).
Online supplemental material
Fig. S1 shows analysis of BB alignment and verification of MTEC conditions after live imaging. Fig. S2 shows analysis of BB orientation and immunofluorescence images of apical actin and apical keratin 8 IFs in MCCs of MTECs. Fig. S3 documents the distribution of apical MTs in MCCs of MTECs revealed by super-resolution confocal microscopy and serial thin-section electron microscopy. Fig. S4 shows effects of drug treatment on BB arrays and apical cytoskeleton. Fig. S5 demonstrates spatial distribution of the cytoskeletal cross-linker plectin in MTEC multiciliated cells. Furthermore, predictive simulation of BB alignment under the regulation of a cell boundary is shown, demonstrating that asymmetric MT distribution controls the direction of BB lines. Video 1 shows beating cilia of GFP-centrin2 MTECs under normal incubation, after live imaging, and during live imaging. Video 2 shows long-term live imaging of GFP-centrin2-labeled BBs in MTEC multiciliated cells for Cell 1 and Cell 2. Video 3 shows tracking of the dynamic behavior of individual BBs in MTEC multiciliated cells. Videos 4–7 show UHVEMT images and 3D reconstruction of apical MTs in the four patterns of BB alignment. Video 8 shows live imaging of GFP-centrin2-labeled BBs in MTEC multiciliated cells under nocodazole treatment and the behavior of BBs when they lack their asymmetric structural component, the basal foot in Odf2 mutant mouse. Videos 9 and 10 show model simulations of the BB pattern in the wild-type cell, in the perturbed condition under nocodazole treatment, and in the absence of BF, respectively. Additional data are available in the JCB DataViewer at http://dx.doi.org/10.1083/jcb.201601023.dv.
Acknowledgments
We are grateful to our laboratory members for helpful discussions, especially A. Tamura, T. Yano, S. Chiba, and Y. Ogura. We especially thank M. Uji and T. Nishida for technical assistance in our laboratory. We appreciate the critical technical assistance of H. Miyagi, H. Takatsuka, and A. Motomura (Olympus). We also thank H. Shiratori, H. Hamada, and T. Uemura for discussions. We particularly thank W. J. Nelson for critical reading.
This research was supported by grants from the Core Research for Evolutional Science and Technology of the Japan Science and Technology Agency (to S. Ishihara and S. Tsukita) and in part by Japan Society for the Promotion of Science Grants-in-Aid for Scientific Research in Innovative Areas (25103008 to S. Ishihara and 24113002 to S. Tsukita) and the “Nanotechnology Platform” project of the Ministry of Education, Culture, Sports, Science, and Technology of Japan (12024046).
The authors declare no competing financial interests.
References
Author notes
E. Herawati and D. Taniguchi contributed equally to this paper.
H. Kanoh's present address is Graduate School of Biostudies, Kyoto University, Kyoto 060-8501, Japan.