The inositol 1,4,5-trisphosphate (IP3) receptor (IP3R) channel is crucial for the generation and modulation of intracellular Ca2+ signals in animal cells. To gain insight into the complicated ligand regulation of this ubiquitous channel, we constructed a simple quantitative continuous-time Markov-chain model from the data. Our model accounts for most experimentally observed gating behaviors of single native IP3R channels from insect Sf9 cells. Ligand (Ca2+ and IP3) dependencies of channel activity established six main ligand-bound channel complexes, where a complex consists of one or more states with the same ligand stoichiometry and open or closed conformation. Channel gating in three distinct modes added one complex and indicated that three complexes gate in multiple modes. This also restricted the connectivity between channel complexes. Finally, latencies of channel responses to abrupt ligand concentration changes defined a model with specific network topology between 9 closed and 3 open states. The model with 28 parameters can closely reproduce the equilibrium gating statistics for all three gating modes over a broad range of ligand concentrations. It also captures the major features of channel response latency distributions. The model can generate falsifiable predictions of IP3R channel gating behaviors and provide insights to both guide future experiment development and improve IP3R channel gating analysis. Maximum likelihood estimates of the model parameters and of the parameters in the De Young–Keizer model yield strong statistical evidence in favor of our model. Our method is simple and easily applicable to the dynamics of other ion channels and molecules.
INTRODUCTION
Ca2+ is one of the most important signaling ions in that it controls numerous cellular functions such as neurotransmitter release, muscle contraction, and nuclear transcription (Berridge et al., 1998). Ca2+ performs such a wide range of tasks through a hierarchy of signaling patterns ranging from single-channel events to waves sweeping over entire organs (Berridge et al., 1998). In many cell types, the inositol 1,4,5-trisphosphate (IP3) receptor (IP3R) Ca2+ release channel plays a central role in orchestrating the hierarchical Ca2+ patterns. Thus, it is crucial to understand the mechanisms regulating the IP3R. Considerable efforts and expertise have gone into modeling the modulation of IP3R channel gating by its main physiological ligands: IP3 and Ca2+ (De Young and Keizer, 1992; Sneyd and Dufour, 2002; Dawson et al., 2003; Mak et al., 2003; Shuai et al., 2007; Gin et al., 2009; Swaminathan et al., 2009). Most of these models can explain the Ca2+ dependence of the open probability (Po) of IP3R. Only the model in Mak et al. (2003) can also accurately reproduce the IP3 dependence of Po, but it required 14 parameters to do so. One of us (Mak) has conducted several studies of the native IP3R channel from insect Sf9 cells, which has a primary sequence most closely related to the type 1 IP3R isoform in vertebrate cells (Foskett et al., 2007), to elucidate various behaviors of the IP3R channel, including the ligand dependence of its Po and mean open- and closed-channel dwell times (τo and τc, respectively), its modal gating behaviors in various ligand concentrations, and the transient response of the channel to rapid changes in ligand concentrations. To date, no model of the IP3R has accounted for all these observations. Here, we propose such a model.
MATERIALS AND METHODS
The many observations mentioned above have enabled us to develop a highly constrained mathematical model for the IP3R channel gating kinetics, with the model structure and all of the parameters inferred directly from experimental data. The model consists of a Markov chain with 3 open states and 9 closed states, and requires 28 parameters. It reproduces the ligand-dependent equilibrium Po, τo, and τc over wide ranges of cytoplasmic free Ca2+ ( ) and IP3 (
) and IP3 ( ) concentrations (Ionescu et al., 2006); the Ca2+ dependence of various modal gating features, including the relative prevalence (the probability of finding the channel in a particular gating mode) and lifetimes of the gating modes of the IP3R channel, and channel Po in each of the gating modes reported in Ionescu et al. (2007); as well as the distributions of the channel response latencies observed after various abrupt changes in the concentrations of one or both of its ligands (Mak et al., 2007).
) concentrations (Ionescu et al., 2006); the Ca2+ dependence of various modal gating features, including the relative prevalence (the probability of finding the channel in a particular gating mode) and lifetimes of the gating modes of the IP3R channel, and channel Po in each of the gating modes reported in Ionescu et al. (2007); as well as the distributions of the channel response latencies observed after various abrupt changes in the concentrations of one or both of its ligands (Mak et al., 2007).
We accomplished this working under the following major assumptions: (a) the model is a finite-state Markov chain, (b) the ligand-binding kinetics obey the law of mass action, (c) the chain is fully connected, (d) the channel must be able to unbind ligands, and (e) the model should be as simple as possible. We show in the supplemental text, section 1.1 (see also Fig. S1), that the gating and binding kinetics of IP3R are consistent with the detailed balance hypothesis.
Structurally, the IP3R channel is an oligomer. However, we do not assume that the IP3R subunits in the channel are independent or that the ligand-binding sites in each subunit are independent. We make no a priori assumption about sequential or independent binding of IP3 and Ca2+ to the channel and therefore are consistent with experimental observations demonstrating that IP3 and Ca2+ bind to the channel cooperatively but with no specific sequential requirements (Mak et al., 2007), unlike many previous models that assumed sequential (Tang et al., 1996; Marchant and Taylor, 1997) or independent (Swillens et al., 1994; Tang et al., 1996; Hirose et al., 1998; Fraiman and Dawson, 2004) IP3 and Ca2+ binding.
Our one structural constraint is to search only over models with four IP3-binding sites. Structure is at most an a priori weak constraint on dynamics. Beece et al. (1980) note that “the protein is not a rigid system in which a ligand moves in a fixed potential. Rather there is a strong mutual interaction between ligand and protein … A protein is not like a solid house into which the visitor (the ligand) enters by opening doors without changing the structure. Rather it is like a tent into which a cow strays.” Another difficulty with structurally motivated models is that they tend to have large numbers of states that cannot be deduced from patch-clamp recordings. Eigen’s “general allosteric model” has 55 states for a tetrameric channel in which each subunit can bind a single ligand and has two major conformations (Eigen, 1968). There is no a priori reason to believe that the IP3R subunits have a particular number of conformations available to them. The IP3R is known to have at least one IP3-binding site and two Ca2+-binding sites per monomer. The same reasoning that led to Eigen’s model would result in an IP3R model with thousands of states. A large Markov chain will not have rates that can be learned from the data because of the large number of parameters that would need to be estimated from data. We believe that there are probably numerous small Markov chains that all yield similar likelihoods for the observed data. Based on the quality of the fit, one can use Markov chain selection criteria to at least select between specific categories of Markov chains. Here, we construct a model with cooperativity in the IP3-binding dynamics. We refer to this model as the “cooperative model” (CM). We compare the likelihood of the data given the CM to the likelihood of the same data given the most frequently used De Young–Keizer model (DYKM) (De Young and Keizer, 1992). The DYKM yields a somewhat higher likelihood for the Po data than the CM (although such was not the case for Xenopus laevis oocyte Po data). We also performed maximum likelihood fits to dynamic data: latency measurements as well as stationary time series. Fits to the latency data only and the combined latency and current trace data indicated that the CM outperforms the DYKM. Thus, the DYKM does a very good job reproducing the Po data from Sf9 cells. However, it does not compete well with the CM when the recent kinetic data are taken into account.
We use the theory of aggregated binary reversible Markov chains (Colquhoun and Hawkes, 1981; Fredkin et al. 1985. Proceedings of the Berkeley Conference in Honor of Jerzy Neyman and Jack Kiefer; Fredkin and Rice, 1986; Qin et al., 1997; Bruno et al., 2005) to derive a model via an iterative, data-driven approach. First, we consider the ligand dependencies of the equilibrium Po, which provides evidence for the main ligand-binding stoichiometric complexes that must be included in a model Markov chain. A stoichiometric complex is specified by the number of Ca2+ ions (m) and IP3 molecules (n) bound to the channel, and by the gating state of the channel (open or closed). The C32 (O32) complex refers to a closed (open) channel bound to three Ca2+ ions and two IP3 molecules. Such complexes can comprise more than one Markovian state (a state in a Markov chain from which the channel exits with time-independent rate constant(s) so that it has a mono-exponential lifetime distribution). The number of such states in a complex cannot be ascertained from ligand dependencies of the Po data, but in the absence of data to the contrary, assumption (e) demands one state per complex. The parameters that can be inferred from Po are the equilibrium occupancies of complexes and contain no information regarding network topology (supplemental text, section 1.2). Nor can the total number of complexes necessarily be inferred from Po. At this stage, if the ligand dependencies of channel Po do not require a particular complex, simplicity demands that the complex not be explicitly included in the chain. Then we consider the Ca2+ dependence of the modal gating behaviors: the relative prevalence of and the channel Po in each of the modes. These data provide evidence for the inclusion of one more complex and suggest that some complexes can be in more than one gating state.
Furthermore, the Ca2+ dependence of the lifetimes of the gating modes provides some broad constraints on the connectivity between the various gating states. Once we have an estimate of the important states in the model and their occupancies, we deduce the full model with additional states and connections, and the rates related to the connections by fitting the response latencies of the channel to abrupt changes in ligand concentrations and current trace data. The full model that we constructed is shown in Fig. 1.
The kinetic scheme for the proposed model. The superscript of each state denotes the gating mode that state is in. The two numbers in the subscripts indicate the number of Ca2+ and IP3, respectively, that is bound to the channel in that state. The model has nine closed states (, , , , , , , , and ) and three open states (, , and ). The elliptical shadings highlight complexes needed to account for the ligand dependencies of the channel Po. The square shading highlights the complex required to fit the modal gating statistics, and the diamond shadings highlight complexes introduced as a result of IP3 activation latency distribution. The transition rates between various states and the related flux parameters are listed in Tables S2 and S3, respectively.
The kinetic scheme for the proposed model. The superscript of each state denotes the gating mode that state is in. The two numbers in the subscripts indicate the number of Ca2+ and IP3, respectively, that is bound to the channel in that state. The model has nine closed states (, , , , , , , , and ) and three open states (, , and ). The elliptical shadings highlight complexes needed to account for the ligand dependencies of the channel Po. The square shading highlights the complex required to fit the modal gating statistics, and the diamond shadings highlight complexes introduced as a result of IP3 activation latency distribution. The transition rates between various states and the related flux parameters are listed in Tables S2 and S3, respectively.
Occupancy and flux
Instead of parameterizing our model with reaction rates, as done in most previous efforts to model the IP3R channel gating, we use “state occupancy” and “flux” parameters as suggested in Yang et al. (2006). The two approaches are mathematically equivalent, but we find the occupancy–flux parameter approach simpler and more intuitive because it separates thermodynamic quantities (equilibrium occupancies) from kinetic quantities (reaction fluxes), or equivalently, it separates reaction rates from equilibrium constants. Occupancy and flux parameters are used also because occupancy determination is far more robust than state lifetime measurements. Failure to detect brief events (channel opening and closing or changing gating modes) can have a large impact on estimates of mean lifetimes of the states but does not affect state occupancy estimates significantly (supplemental text, section 1.3, and Fig. S2). Furthermore, the normalized occupancies are just rational functions of ligand. Thus, once the occupancies are learned by fitting the Po function to the data (described below), they are fixed throughout the subsequent data-fitting process. This constraint is trivial to apply using occupancy parameters: we simply do not alter the occupancy parameters unless it can be done without significantly affecting channel Po. Details of occupancy and flux parameters are given in the supplemental text, section 1.4.
Low occupancy states
Another concept that we required is the notion of short-lived low occupancy states (Ullah et al., 2012). The Po data suggest that there are complexes with no IP3 bound and complexes with four IP3 bound. Clearly there must be complexes with one, two, and three IP3 bound, but our analysis of channel Po provides little evidence for them. We conclude that these states exist, but their occupancies are not high enough for them to be detected in the Po data. Such low occupancy transition states are not included explicitly in the model and their occupancies are set to zero to satisfy the maximal simplicity assumption. Similarly, some complexes with no Ca2+ bound are linked directly to complexes with two Ca2+ bound in the model. However, the effects of these transition states are manifested in the particular functional form for the fluxes passing through them imposed by mass action and detailed balance. Proper treatment of low occupancy states is crucial, both for getting the rates right in the simplified model and for obtaining a model structure with learnable parameters. Applying such simplifications by excluding low occupancy states can result in a substantial reduction in the number of parameters required. More details regarding low occupancy states are given in the supplemental text, section 1.5. In the supplemental text, section 1.6, we derive the functional form of the transition rates between various model states (Fig. 1) and simplify the branches that involve low occupancy states by eliminating these states.
Complex occupancies
We identify the relevant (high occupancy) complexes from the ligand dependencies of channel Po. Relative to the reference unliganded closed complex C00, the occupancies of the Cmn and Omn complexes are proportional to  , with occupancy parameters
, with occupancy parameters
, respectively. One can choose any complex as a reference complex, but we found the unliganded complex to be the simplest. The occupancy parameter of a complex is the sum over all the states contained in the complex of the products of equilibrium association constants along any path connecting C00 to each state (). The normalized occupancy of Cmn and Omn are

respectively, where Z, the total occupancy over all states, is given by

with mmax and nmax being the maximum number of Ca2+ and IP3 that the channel can bind. The equilibrium Po function is:

Our initial Po-based search resulted in a best-fit (according to the AIC score; Mcquarrie, 1998) model with five closed complexes (C00, C04, C24, C32, and C34) and one open complex (O24) (Fig. 1). We first used the Mathematica routine “NonlinearModelFit,” which does least squares and assumes a constant variance, meaning that it assumed the Po function was Gaussian distributed with constant variance. We also assumed a variance proportional to Po (1-Po) and found little difference. Both distribution functions for the Po data returned similar models. The fit to the Po data are shown in Fig. 2. Although not essential to the Po fit, the O14 complex is necessary to account for the Ca2+ dependence of channel Po in the I gating mode (mode with intermediate Po; see Modal occupancies). The C20 and C30 complexes are required to account for the latency distribution observed (see Model development using latencies), but the occupancies of these two complexes are so low that they do not contribute significantly to Po or affect the quality of the Po fits in Fig. 2. Theoretically, the Po can be expressed as a function of the eight occupancy parameters of the nine complexes (occupancy of the reference C00 complex is 1). However, the terms 1,

are all small relative to the other terms in Z for the values of  used in the Po measurements, and O14 complex is only required for the channel Po in I mode. This implies that the Po is effectively determined by the five occupancy parameters for the complexes with IP3 bound
used in the Po measurements, and O14 complex is only required for the channel Po in I mode. This implies that the Po is effectively determined by the five occupancy parameters for the complexes with IP3 bound
We took the occupancy parameters to be as small as possible without altering our estimate of the Po.
Ca2+ dependence of IP3R channel Po. Channel Po under IP3 concentration of 10 µM (bullets and solid line), 100 nM (squares and dashed line), 33 nM (triangles and dotted line), and 10 nM (diamonds and dotted-dashed line). The symbols represent mean experimental Po, error bars represent standard errors of the mean, and lines are theoretical fits. The experimental data are taken from Ionescu et al. (2006) (supplemental text, section 1.10.1).
Ca2+ dependence of IP3R channel Po. Channel Po under IP3 concentration of 10 µM (bullets and solid line), 100 nM (squares and dashed line), 33 nM (triangles and dotted line), and 10 nM (diamonds and dotted-dashed line). The symbols represent mean experimental Po, error bars represent standard errors of the mean, and lines are theoretical fits. The experimental data are taken from Ionescu et al. (2006) (supplemental text, section 1.10.1).
Subsequent searches yielded other models with better AIC scores (for the fit to Sf9 Po data) than the one we discuss here. However, we were unable to account for the modal gating statistics using these other models. One such model that gave a better AIC score on the Sf9 Po data was DYKM. However, the CM performed better than the DYKM when fitted to the Po data from Xenopus oocytes (see Comparison between the CM and the DYKM). The value of
that we ended up with gives the geometric mean for the IP3 affinities along the path connecting C00 to C04 of ∼8 nM. The numerical values of the occupancy parameters are given in Table S1. In the remainder of this article, we construct a model based on these complexes.
Modal occupancies
The Sf9 IP3R channel exhibits three distinct gating patterns or modes: a quiescent L mode with low Po in which brief openings are separated by long quiescent periods with long τo, an I mode with intermediate Po in which the channel opens and closes rapidly with short τc and τo, and an H mode with high Po in which the channel gates in bursts (Ionescu et al., 2007). All three modes are observed under all conditions for which the channel gates, and the channel spontaneously changes among all three modes, even under constant ligand conditions (Fig. 3 A). The gating characteristics of the channel (Po, τc, and τo) remain remarkably consistent in each gating mode in all ligand conditions so the ligand dependencies of overall channel Po, τc, and τo come from the ligand dependencies of the relative prevalence (or normalized occupancies), πM, of the gating modes (M can be L for low mode, I for intermediate mode, and H for high mode) (Ionescu, et al., 2007). The key modal statistical data at our disposal are shown in Fig. 4. Each of the three plots shows nine data points corresponding to  = 0.1, 1, and 89 µM (
= 0.1, 1, and 89 µM ( = 10 µM for all data). The squares, bullets, and triangles in Fig. 4 represent the L, M, and H modes, respectively. To account for these observed modal gating behaviors, we have to extend our minimal model by splitting some complexes into two states when required, without adding new complexes other than O14, which is required for the channel Po in I mode.
= 10 µM for all data). The squares, bullets, and triangles in Fig. 4 represent the L, M, and H modes, respectively. To account for these observed modal gating behaviors, we have to extend our minimal model by splitting some complexes into two states when required, without adding new complexes other than O14, which is required for the channel Po in I mode.
Modal gating time series. (A) Single-channel current record of IP3R channel gating in the presence of  = 1 µM and
= 1 µM and  = 10 µM. (B) Simulated binary on/off single-channel current record generated from the model. The squares, bullets, and triangles indicate a transition to the L, I, and H gating mode, respectively.
= 10 µM. (B) Simulated binary on/off single-channel current record generated from the model. The squares, bullets, and triangles indicate a transition to the L, I, and H gating mode, respectively.
Modal gating time series. (A) Single-channel current record of IP3R channel gating in the presence of  = 1 µM and
= 1 µM and  = 10 µM. (B) Simulated binary on/off single-channel current record generated from the model. The squares, bullets, and triangles indicate a transition to the L, I, and H gating mode, respectively.
= 10 µM. (B) Simulated binary on/off single-channel current record generated from the model. The squares, bullets, and triangles indicate a transition to the L, I, and H gating mode, respectively.
Ca2+ dependence of IP3R channel modal behavior. (A) Channel open probability in various gating modes, (B) relative prevalence πM, and (C) mean lifetimes τM of the various modes (M can be L, I, or H). Symbols and curves represent the mean modal gating characteristics and theoretical fits, respectively. Symbols and curves for different modes are: triangles and solid lines, H; bullets and dashed lines, I; squares and dotted lines, L. Error bars in A–C are smaller than the symbols. The experimental data are taken from Ionescu et al. (2007) (supplemental text, section 1.10.2).
Ca2+ dependence of IP3R channel modal behavior. (A) Channel open probability in various gating modes, (B) relative prevalence πM, and (C) mean lifetimes τM of the various modes (M can be L, I, or H). Symbols and curves represent the mean modal gating characteristics and theoretical fits, respectively. Symbols and curves for different modes are: triangles and solid lines, H; bullets and dashed lines, I; squares and dotted lines, L. Error bars in A–C are smaller than the symbols. The experimental data are taken from Ionescu et al. (2007) (supplemental text, section 1.10.2).
Fig. 4 A shows the conditional open probabilities, , within each mode. and are nearly independent of  (≈0.007 and 0.8, respectively), whereas exhibits biphasic Ca2+ dependence: rising from ∼0.2 at
(≈0.007 and 0.8, respectively), whereas exhibits biphasic Ca2+ dependence: rising from ∼0.2 at  = 100 nM to 0.3 at
= 100 nM to 0.3 at  = 1 µM, and then dropping back to 0.2 at
= 1 µM, and then dropping back to 0.2 at  = 89 µM.
= 89 µM.
Because of the ligand independence of , we postulated that the H mode comprises two states, and , so

where we have split the C24 complex into and states, and the O24 complex into and states (also see next paragraph). Any combination of open and closed states (at least one open and one closed state) with the same number of  and
and  bound would give ligand-independent . The only such combination available in the model is of states with two
bound would give ligand-independent . The only such combination available in the model is of states with two  and four
and four  bound. Considering any other combination would require adding more states to the model, which is not warranted by our simplicity assumption.
bound. Considering any other combination would require adding more states to the model, which is not warranted by our simplicity assumption.
If the I mode contains only states with two Ca2+ and four IP3 bound, will also be ligand independent. Thus, we postulate the O14 complex besides the C24 and O24 complexes are in the I mode. However, this will only give monotonically rising as  is increased. Adding a state can generate a biphasic dependence of on
is increased. Adding a state can generate a biphasic dependence of on  , but will cause the relative prevalence of the I mode (πI) to increase with increasing
, but will cause the relative prevalence of the I mode (πI) to increase with increasing  (Fig. S4), which is not observed (Fig. 4 B). Thus, the peak in necessitates the state besides , , and , so
(Fig. S4), which is not observed (Fig. 4 B). Thus, the peak in necessitates the state besides , , and , so

Here, we have split the C04 complex into and states, as required by the observation regarding I and L modes, and = O14. Adding the O14 complex worsens the AIC score for the model fit to the Po data (Fig. 2) by 1 but improves the quality of the fit by improving the log likelihood (see Eq. 5 below). Adding any other open states such as O04 or O34 worsens both the AIC and log-likelihood scores by a factor much higher than 1.
According to the AIC and BIC criteria (Mcquarrie, 1998), there is insufficient justification from experimental evidence to assume that the C34, C32, and C00 complexes consist of more than one state. For example, splitting the C34 complex into two states will add one more parameter to the model and will increase the AIC score by a factor of 2 (see the factor 2k in Eq. 5 below), without changing the Po given by the model (Eq. 2). So we assign them as , , and to satisfy the simplicity assumption.
Fig. 4 B shows the Ca2+ dependence of πM = ZM/Z. A fit of the Po data in various  and
and  (curves in Fig. 2) followed by fits to the and πM data in different
(curves in Fig. 2) followed by fits to the and πM data in different  (curves in Fig. 4, A and B, respectively) using the Mathematica routine NonlinearModelFit (see Complex occupancies) determines the values of the occupancy parameters for the various states in the three gating modes.
(curves in Fig. 4, A and B, respectively) using the Mathematica routine NonlinearModelFit (see Complex occupancies) determines the values of the occupancy parameters for the various states in the three gating modes.
By this point, the number of states in the model and the occupancy parameters have been determined. We will determine the connections between these states guided by the observed modal lifetimes and latency distributions. We will evaluate all possible connections and choose only those that lead to the observed behavior of the channel.
Modal lifetimes
Some, but not all, connectivities between the various states can be inferred from the observed modal gating behaviors. Channel opening and closing events were observed as the channel remained in the same mode; therefore, there are direct connections between and , and between and . Furthermore, the three modes are all connected to allow modal changes among the three modes (Ionescu et al., 2007).
The mean H mode lifetime, τH, has a maximum as a function of  (Fig. 4 C, triangles). This suggested that the H mode is connected to to yield a short τH at high
(Fig. 4 C, triangles). This suggested that the H mode is connected to to yield a short τH at high  . We also connect the H mode to so the rate from the H mode to increases and τH decreases with decreasing
. We also connect the H mode to so the rate from the H mode to increases and τH decreases with decreasing  . It should be noted that although moving from the H mode to the state involves Ca2+ dissociation from the channel, the effective rate of the reaction is
. It should be noted that although moving from the H mode to the state involves Ca2+ dissociation from the channel, the effective rate of the reaction is  dependent (see Low occupancy states). The state is connected to the state to account for the τL and τI in low
dependent (see Low occupancy states). The state is connected to the state to account for the τL and τI in low  . The long τL (Fig. 4 C, ∼ 3 s) indicates a low rate from to .
. The long τL (Fig. 4 C, ∼ 3 s) indicates a low rate from to .
Finally, we connect the I and H mode open states via Ca2+-independent rates to get the appropriate H mode lifetime under optimal ligand conditions. Further determination of the connectivity of the model requires consideration of channel response latencies (see Model development using latencies).
The remaining connections and the final values of the flux parameters will be determined below using the fit to the latency and time-series data.
Model development using latencies
 and
and  on the cytosolic side of the IP3R channel were abruptly changed in nuclear patch-clamp experiments in the cytoplasmic-side-out configuration using rapid perfusion solution exchange techniques to observe the latencies for the response of the channel to ligand concentration changes (Mak et al., 2007).
on the cytosolic side of the IP3R channel were abruptly changed in nuclear patch-clamp experiments in the cytoplasmic-side-out configuration using rapid perfusion solution exchange techniques to observe the latencies for the response of the channel to ligand concentration changes (Mak et al., 2007).  was changed among low (<10 nM, which we will refer to as 0 for notational simplicity), optimal (2 µM) and inhibitory (300 µM) levels, and
was changed among low (<10 nM, which we will refer to as 0 for notational simplicity), optimal (2 µM) and inhibitory (300 µM) levels, and  between 0 and high (10 µM) levels. (
between 0 and high (10 µM) levels. ( ,
,  ) were switched from nonactivating (2 µM, 0), (0, 10 µM), and (0, 0) to optimal (2 µM, 10 µM) to measure IP3 activation, Ca2+ activation, and Ca2+ and IP3 activation latencies, respectively. To measure corresponding deactivation latencies, (
) were switched from nonactivating (2 µM, 0), (0, 10 µM), and (0, 0) to optimal (2 µM, 10 µM) to measure IP3 activation, Ca2+ activation, and Ca2+ and IP3 activation latencies, respectively. To measure corresponding deactivation latencies, ( ,
,  ) were changed from optimal back to various nonactivating combinations. Vertebrate IP3R channels exhibit spontaneous activity in (0, 0) (Mak et al., 2003). However, the insect Sf9 IP3R does not exhibit such spontaneous activity (Mak et al., 2007), so the Ca2+ and Ca2+ and IP3 activation and deactivation latencies can be unambiguously determined. (
) were changed from optimal back to various nonactivating combinations. Vertebrate IP3R channels exhibit spontaneous activity in (0, 0) (Mak et al., 2003). However, the insect Sf9 IP3R does not exhibit such spontaneous activity (Mak et al., 2007), so the Ca2+ and Ca2+ and IP3 activation and deactivation latencies can be unambiguously determined. ( ,
,  ) were changed from optimal to inhibitory (300 µM, 10 µM) and from (300 µM, 10 µM) to optimal to measure latencies of inhibition and recovery from inhibition, respectively. Latencies after activating or recovery solution switches are the durations between solution switches and the first observed openings of the channel in response to the changes, whereas latencies after deactivating or inhibitory solution switches are the durations from the switches to the last observed closings of the channel as its activity terminated. Histograms of these latencies were built up from repeated solution switches in multiple experiments as shown in Fig. 5.
) were changed from optimal to inhibitory (300 µM, 10 µM) and from (300 µM, 10 µM) to optimal to measure latencies of inhibition and recovery from inhibition, respectively. Latencies after activating or recovery solution switches are the durations between solution switches and the first observed openings of the channel in response to the changes, whereas latencies after deactivating or inhibitory solution switches are the durations from the switches to the last observed closings of the channel as its activity terminated. Histograms of these latencies were built up from repeated solution switches in multiple experiments as shown in Fig. 5.
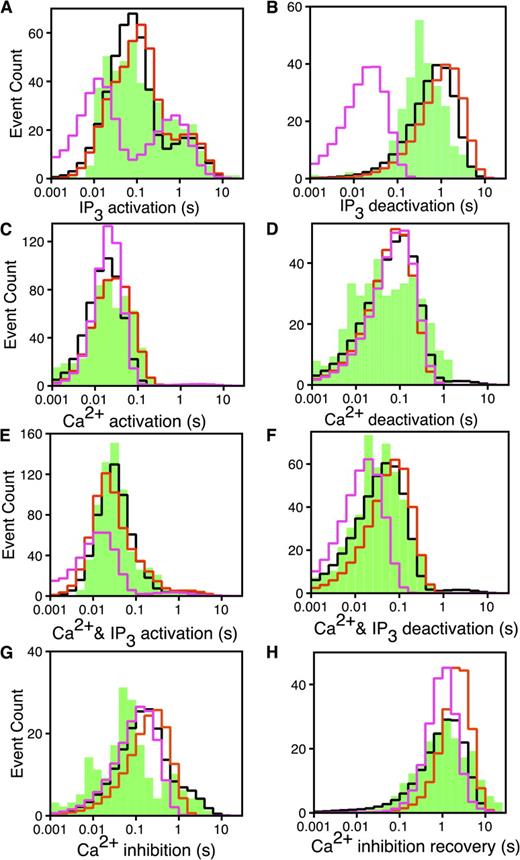
Logarithmically binned latency histograms of IP3R channels responding to changes in  and
and  . In each case, (
. In each case, ( ,
,  ) are changed as indicated: (A) IP3 activation: (2 µM, 0 µM) → (2 µM, 10 µM). (B) IP3 deactivation: (2 µM, 10 µM) → (2 µM, 0 µM). (C) Ca2+ activation: (0 µM, 10 µM) → (2 µM, 10 µM). (D) Ca2+ deactivation: (2 µM, 10 µM) → (0 µM, 10 µM). (E) Ca2+ and IP3 activation: (0 µM, 0 µM) → (2 µM, 10 µM). (F) Ca2+ and IP3 deactivation: (2 µM, 10 µM) → (0 µM, 0 µM). (G) Ca2+ inhibition: (2 µM, 10 µM) → (300 µM, 10 µM). (H) Ca2+ inhibition recovery: (300 µM, 10 µM) → (2 µM, 10 µM). The experimental latency distributions given by the bars are taken from Mak et al. (2007). The solid and dotted lines, respectively, are from the CM when fit to the latency data alone and to the latency and time-series data simultaneously.
) are changed as indicated: (A) IP3 activation: (2 µM, 0 µM) → (2 µM, 10 µM). (B) IP3 deactivation: (2 µM, 10 µM) → (2 µM, 0 µM). (C) Ca2+ activation: (0 µM, 10 µM) → (2 µM, 10 µM). (D) Ca2+ deactivation: (2 µM, 10 µM) → (0 µM, 10 µM). (E) Ca2+ and IP3 activation: (0 µM, 0 µM) → (2 µM, 10 µM). (F) Ca2+ and IP3 deactivation: (2 µM, 10 µM) → (0 µM, 0 µM). (G) Ca2+ inhibition: (2 µM, 10 µM) → (300 µM, 10 µM). (H) Ca2+ inhibition recovery: (300 µM, 10 µM) → (2 µM, 10 µM). The experimental latency distributions given by the bars are taken from Mak et al. (2007). The solid and dotted lines, respectively, are from the CM when fit to the latency data alone and to the latency and time-series data simultaneously.
Logarithmically binned latency histograms of IP3R channels responding to changes in  and
and  . In each case, (
. In each case, ( ,
,  ) are changed as indicated: (A) IP3 activation: (2 µM, 0 µM) → (2 µM, 10 µM). (B) IP3 deactivation: (2 µM, 10 µM) → (2 µM, 0 µM). (C) Ca2+ activation: (0 µM, 10 µM) → (2 µM, 10 µM). (D) Ca2+ deactivation: (2 µM, 10 µM) → (0 µM, 10 µM). (E) Ca2+ and IP3 activation: (0 µM, 0 µM) → (2 µM, 10 µM). (F) Ca2+ and IP3 deactivation: (2 µM, 10 µM) → (0 µM, 0 µM). (G) Ca2+ inhibition: (2 µM, 10 µM) → (300 µM, 10 µM). (H) Ca2+ inhibition recovery: (300 µM, 10 µM) → (2 µM, 10 µM). The experimental latency distributions given by the bars are taken from Mak et al. (2007). The solid and dotted lines, respectively, are from the CM when fit to the latency data alone and to the latency and time-series data simultaneously.
) are changed as indicated: (A) IP3 activation: (2 µM, 0 µM) → (2 µM, 10 µM). (B) IP3 deactivation: (2 µM, 10 µM) → (2 µM, 0 µM). (C) Ca2+ activation: (0 µM, 10 µM) → (2 µM, 10 µM). (D) Ca2+ deactivation: (2 µM, 10 µM) → (0 µM, 10 µM). (E) Ca2+ and IP3 activation: (0 µM, 0 µM) → (2 µM, 10 µM). (F) Ca2+ and IP3 deactivation: (2 µM, 10 µM) → (0 µM, 0 µM). (G) Ca2+ inhibition: (2 µM, 10 µM) → (300 µM, 10 µM). (H) Ca2+ inhibition recovery: (300 µM, 10 µM) → (2 µM, 10 µM). The experimental latency distributions given by the bars are taken from Mak et al. (2007). The solid and dotted lines, respectively, are from the CM when fit to the latency data alone and to the latency and time-series data simultaneously.
Additional experiments were performed in which ( ,
,  ) was switched from (0, 10 µM) to (300 µM, 10 µM) and back. In most of these switches, a burst of channel activity was observed before the channel was inhibited by high
) was switched from (0, 10 µM) to (300 µM, 10 µM) and back. In most of these switches, a burst of channel activity was observed before the channel was inhibited by high  . But in 9 out of 103 switches, no channel open activity was observed. When
. But in 9 out of 103 switches, no channel open activity was observed. When  was decreased from 300 µM to 0, the channel was transiently activated in only 6 out of 94 experiments (Mak et al., 2007). These observations indicate that has a direct connection to without passing through the O24 complex.
was decreased from 300 µM to 0, the channel was transiently activated in only 6 out of 94 experiments (Mak et al., 2007). These observations indicate that has a direct connection to without passing through the O24 complex.
Both the distributions of the inhibitory and inhibition recovery latencies after ( ,
,  ) switching between (2 µM, 10 µM) and (300 µM, 10 µM) can be fitted with single-exponential curves with no deficit of short latencies (Mak et al., 2007). This suggests that the state is directly connected to the state.
) switching between (2 µM, 10 µM) and (300 µM, 10 µM) can be fitted with single-exponential curves with no deficit of short latencies (Mak et al., 2007). This suggests that the state is directly connected to the state.
The Ca2+ and IP3 activation latencies are short (Fig. 5 E), indicating that is directly connected to without going through because rate from to is too slow, as revealed by long τL. Moreover, deficit in short latencies (<20 ms) for Ca2+ and IP3 activation and Ca2+ activation (Mak et al., 2007) suggests that is not directly connected to . Thus, it should be connected to .
Furthermore, to satisfy assumption (d) and allow IP3 unbinding from the and states when  is dropped to 0 in
is dropped to 0 in  = 300 µM, we postulate that is not a transition state, and it must be connected to through . Similarly, to allow Ca2+ to unbind from in the absence of IP3, it must be connected to through ; and to allow Ca2+ to unbind from , it must be connected to .
= 300 µM, we postulate that is not a transition state, and it must be connected to through . Similarly, to allow Ca2+ to unbind from in the absence of IP3, it must be connected to through ; and to allow Ca2+ to unbind from , it must be connected to .
The three distinguishable peaks in the IP3 activation latency distribution (Fig. 5 A) require at least three pathways connecting the closed states with no IP3 bound to the state. Thus, we include in our model one more closed state, , besides the and states. is connected to to maintain the deficit in short latencies for IP3 activation.
Finally, to provide two pathways for the open states to reach to account for the two peaks in the logarithmically binned latency histogram for Ca2+ deactivation (Fig. 5 D), is connected to . At this point, we have inferred the occupancies of all 12 Markovian states and the connections shown in our final model (Fig. 1) based on experimental observations. This completes the determination of states and the connections between various states in the model.
Next, we will determine the values of flux parameters involved in the transition rates between various states by fitting the model to the latency and time-series data. First, we set the initial values of flux parameters in all reactions, as described in the supplemental text, section 1.7. We will use these values as initial conditions for the global fit to the latency and time-series data described below. Although we estimate the initial values of flux parameters from observations, the initial guess proved unnecessary for the fit. The fit converged to the same final parameter values for random initial conditions.
Maximum likelihood and AIC calculations
To determine various flux parameters, we performed maximum likelihood fits on current traces of channel gating under constant conditions of  = 10 µM and
= 10 µM and  = 0.1, 1, and 89 µM, and on the latency data. To accomplish this task, we used our own implementation and calculated the relevant “log-likelihood” functions for the CM in the open-source programming language “Octave.” We used the function “nelder_mead_min” in the optimization tool kit to minimize the likelihood scores (−log(likelihood(data))) of the latency and time-series data by varying the 18 free flux parameters (while holding the occupancy parameters fixed).
= 0.1, 1, and 89 µM, and on the latency data. To accomplish this task, we used our own implementation and calculated the relevant “log-likelihood” functions for the CM in the open-source programming language “Octave.” We used the function “nelder_mead_min” in the optimization tool kit to minimize the likelihood scores (−log(likelihood(data))) of the latency and time-series data by varying the 18 free flux parameters (while holding the occupancy parameters fixed).
The (negative) of the logarithm of the likelihood function for the latency data are minus the sum of the logarithms of the likelihoods of all the latencies:
where is the probability density function for latency and is explained in the next section. Rather than varying the rates and constraining them to be positive, we varied the log base 10 of the parameters without constraint. As discussed in the next section, involves the generator matrix. It is shown in the supplemental text, section 1.2, that when detailed balance is obeyed, the generator matrix is similar to a symmetric matrix. We performed the symmetrizing similarity transformation on the generator matrix whenever all the occupancies relevant to a given experiment were nonzero. This improves the condition number for eigenvalue calculations (see section 8.2 in Cheney and Kincaid, 2007).
For the current traces, we calculated the log of the likelihood function:
where πC is the initial probability of closed states being occupied at equilibrium, toi and tci are the ith opening and closing in the time series, respectively, and is a matrix of the transition rates from all open to all closed states, etc. For the CM, this was accomplished as described in Qin et al. (1997). We could not use QUB (Qin et al., 1997) for this because of the complex form of our rates. Nor could we perform a brute force search through the trillions of candidate model topologies using QUB. Similarly for the DYKM, we could not use QUB because of the complex form of the 120-state model (see Comparison between the CM and the DYKM for details about DYKM). For data obtained at equilibrium, with , where uc is an Nc (the number of close states) component vector of all 1’s. wC and wO are the equilibrium occupancies of the closed and open states, respectively. For the CM, NC = 9 and the number of open states, NO = 3. Thus QCC, QOO, QCO, and QOC are 9 × 9, 3 × 3, 9 × 3, and 3 × 9 matrices, respectively.
We did two different fits: one in which we fit to all the latency data and none of the time-series data, and a second in which we fit both the latency data and the time-series data. The total log likelihood of all data used in the fit was calculated as
where Nexp is the number of experiments, and datai is the dataset (latencies or time series) from experiment i. There are eight latency experiments where each experiment consists of hundreds of trials and each trial represents a latency measurement. The time-series data consists of three experiments (each experiment results in one time series), one each for  = 0.1, 1, and 89 µM. Finally, the AIC score is given by
= 0.1, 1, and 89 µM. Finally, the AIC score is given by
where k is the number of parameters in the model. The CM has 10 occupancy and 18 flux parameters (k = 28).
To minimize the number of parameters, we assume that the effective rates for the reactions , , and are the same. Similarly, the effective rates for the reactions , , and are the same. Relaxing these constraints does not improve the fit to the data. The functional form of various transition rates for the CM is given in Table S2. Parameter values obtained from the fits to the latency data alone and latency plus time-series data are given in Table S3.
Online supplemental material
The supplemental text provides a more in-depth discussion and derivation of various statements made in the main text. In sections 1.1, 1.2, and 1.3, respectively, we show that the IP3R obeys detailed balance (Fig. S1), the equilibrium occupancy data contain no information about the network connectivity, and missing events cause more error in τo and τc (Fig. S2). Sections 1.4, 1.5, 1.6, and 1.7 discuss the concepts of occupancy and probability flux, low occupancy states, simplification of the model, and parameter estimation, respectively, in detail. The derivation of mathematical expressions for τo and τc, and dwell-time distributions are given in sections 1.8 and 1.9. The experimental methods are described in section 1.10. Fig. S3 plots the ligand dependence of some rates in the model, and Fig. S4 proves that state cannot be included in the I mode. Fig. S5 shows that the mean IP3 activation latency has a minimum at intermediate  value. The parameters and transition rates for the CM are given in Tables S1–S3, whereas those for the DYKM are given in Tables S4 and S5. The supplemental material is available.
value. The parameters and transition rates for the CM are given in Tables S1–S3, whereas those for the DYKM are given in Tables S4 and S5. The supplemental material is available.
RESULTS
Fitting modal lifetimes with the model
To reproduce the observed modal lifetimes (Fig. 4 C, τM) with our model, τM are expressed in terms of the occupancy and flux parameters in the model. In general, the lifetime τX of any aggregate X (complex, mode, or other combinations of Markovian states) in an aggregated Markov chain is given by
where ZX is the unnormalized occupancy of aggregate X, and JX is the unnormalized flux out of that aggregate. JX is the sum of all the fluxes from all reactions from all Markovian states contained in the aggregate X to Markovian states not contained in X, so
where is summing over all Markovian states S in the aggregate X, is summing over all Markovian states U that are not in X, and rSU is the rate from a state S to a state U (supplemental text, section 1.6, and Table S2). The modal lifetimes given by the model are shown by the lines in Fig. 4 C.
Fitting latency distributions with the model
To use the CM to account for the distributions of latencies observed in the rapid perfusion solution exchange experiments, we express the latencies in terms of occupancy and flux parameters. When the perfusion solution to which the channel is exposed is changed at time t = 0, the system is initially in an aggregate X containing NX states. As time goes by, it will transition into another aggregate Y with NY states, which is disjoint from X. We assume that NX + NY = N, the total number of states in the system. If Q is the generator matrix for the full system, we partition Q as
Using the formulation developed above, the ij element in Q is Jij/Zi. At time t = 0, the occupancies of initial states (all states in X) are specified in the vector of initial normalized occupancies π(0). Let uX and uY be the NX and NY component vectors, respectively, in which all elements are 1, so π(0)uX = 1. The probability density function for the latency can be expressed as (Colquhoun and Hawkes, 1981; Fredkin et al. 1985. Proceedings of the Berkeley Conference in Honor of Jerzy Neyman and Jack Kiefer; Qin et al., 1997; Bruno et al., 2005):
and the probability value, , for each bin (between t = tmin and tmax) in the model latency histograms . The best fits to the latency distributions obtained by maximizing the likelihood of the latency data are shown by solid lines in Fig. 5. We also performed a maximum likelihood estimate of the parameters using the latency data and stationary time series shown by dotted lines in Fig. 5.
We apply this to our measurement of IP3 channel response latencies, taking care to choose states X and Y, as well as the initial occupancy vector π(0) correctly, i.e., knowing the set of states in which the channel gates before and after the jump in the solution to which the channel is exposed. For activation and recovery from inhibition latencies, the choices of X and Y are more straightforward. The experiment starts with the channel being closed, and the latency is the time until the first channel opening as the channel enters an open state after the change of  and/or
and/or  . Thus, for activation and recovery from inhibition experiments, the aggregate X contains the nine closed states in the CM, tabulated in related matrices and vectors in this order: , , , , , , , , . The aggregate Y contains the three open states tabulated in matrices and vectors in this order: , , and . π(0) is a vector having the initial normalized occupancies of the closed states. For the deactivation latencies, X is composed of , , , , and , and the remaining states are included in the aggregate Y.
. Thus, for activation and recovery from inhibition experiments, the aggregate X contains the nine closed states in the CM, tabulated in related matrices and vectors in this order: , , , , , , , , . The aggregate Y contains the three open states tabulated in matrices and vectors in this order: , , and . π(0) is a vector having the initial normalized occupancies of the closed states. For the deactivation latencies, X is composed of , , , , and , and the remaining states are included in the aggregate Y.
For IP3 activation in constant 2 µM Ca2+, the logarithmically binned histogram for experimental latencies (Fig. 5 A, bars) has three peaks, the main one at ∼80 ms and two minor ones at ∼250 ms and 2 s (Mak et al., 2007), thus giving a mean IP3 activation latency of ∼500 ms, even though the majority of the activation latencies are shorter than 100 ms. This indicates that the Markovian model for ligand regulation of IP3R channel has at least three distinct branches involved in IP3 activation (Mak et al., 2007). This is a natural feature of the CM. With  = 2 µM,
= 2 µM,

where

because only the , , and states are occupied in the absence of IP3. The state is the predominantly occupied one from which the channel can be activated with short latencies by rapidly binding four IP3, transiting through to . Longer latencies can be caused by channels initially occupying the and states being activated with longer latencies. Instead, it generates a distribution with one peak at ∼80 ms for activating the channel from both and states, and another peak ∼2 s corresponding to the channel going from via either or to , which evidently takes a long time as a result of the slow release of the third Ca2+.
To fit the IP3 deactivation latency histogram (Fig. 5 B), we assume that the initial occupancies of the states are their equilibrium occupancies in  = 10 µM and
= 10 µM and  = 2 µM. The case of Ca2+ activation in constant
= 2 µM. The case of Ca2+ activation in constant  (10 µM) is trickier and requires detailed consideration of the manner in which the experiments were performed. In an activation measurement,
(10 µM) is trickier and requires detailed consideration of the manner in which the experiments were performed. In an activation measurement,  was switched from <10 nM to 2 µM.
was switched from <10 nM to 2 µM.  was not returned to <10 nM until ∼2 s after channel activity was detected to ensure that the channel was really activated. Similarly, in a deactivation measurement, ∼2 s was allowed after the last channel opening before
was not returned to <10 nM until ∼2 s after channel activity was detected to ensure that the channel was really activated. Similarly, in a deactivation measurement, ∼2 s was allowed after the last channel opening before  was switched to 2 µM again, to confirm that the channel was really deactivated. We assume that for all Ca2+ activation measurements, the channel only occupies the state before the
was switched to 2 µM again, to confirm that the channel was really deactivated. We assume that for all Ca2+ activation measurements, the channel only occupies the state before the  jumps because it does not have time to transit from to before the solution switches; i.e., the mean transition time between states and is longer than the wait time for switching
jumps because it does not have time to transit from to before the solution switches; i.e., the mean transition time between states and is longer than the wait time for switching  . There were instances in the Ca2+ activation experiments when the channel failed to go active. These failures to activate might have been caused by the IP3R residing in state at the time of the fluid switch. After the solution switch, the rates in QXX and QXY were set in accord with
. There were instances in the Ca2+ activation experiments when the channel failed to go active. These failures to activate might have been caused by the IP3R residing in state at the time of the fluid switch. After the solution switch, the rates in QXX and QXY were set in accord with  = 2 µM and
= 2 µM and  = 10 µM (Fig. 5 C).
= 10 µM (Fig. 5 C).
The Ca2+ deactivation latency histogram has two distinct peaks (Fig. 5 D). The CM fails to capture this feature even though it has two distinct pathways of deactivation: one from and another from . To attempt to improve the fit by relaxing the restriction of considering the rate from = rate from (see Maximum likelihood and AIC calculations in Materials and methods, and supplemental text, section 1.6) does not provide enough improvement in log likelihood for the deactivation latency fit to justify the extra parameters. It is possible that the two peaks corresponding to the two deactivation pathways in the CM cannot be resolved because the model peaks are broadened by having too many short latencies as a result of the exclusion of transition states used in the CM.
For Ca2+ and IP3 activation, the channel initially can only occupy the state with both  and
and  = 0. The CM generates Ca2+ and IP3 activation and deactivation latency distributions that capture the general shape of the experimental distributions (Fig. 5, E and F).
= 0. The CM generates Ca2+ and IP3 activation and deactivation latency distributions that capture the general shape of the experimental distributions (Fig. 5, E and F).
For Ca2+ inhibition, π(0) is set to the normalized occupancies of states , , , , and at  = 10 µM and
= 10 µM and  = 2 µM. For recovery from inhibition, only two inhibited states ( and ) are initially occupied at their equilibrium occupancy at
= 2 µM. For recovery from inhibition, only two inhibited states ( and ) are initially occupied at their equilibrium occupancy at  = 10 µM and
= 10 µM and  = 300 µM. Our fit to the Ca2+ inhibition latencies is unimpressive (Fig. 5 G). The observed inhibition latency distribution has at least two peaks, and the peaks are substantially sharper than the model distribution. The CM has only a single inhibition pathway that is characterized by a single flux parameter. Increasing the flux parameter to obtain a better fit for the inhibition latencies will shift the peak of the inhibition recovery latencies (Fig. 5 H) from the CM by the same amount in the same direction.
= 300 µM. Our fit to the Ca2+ inhibition latencies is unimpressive (Fig. 5 G). The observed inhibition latency distribution has at least two peaks, and the peaks are substantially sharper than the model distribution. The CM has only a single inhibition pathway that is characterized by a single flux parameter. Increasing the flux parameter to obtain a better fit for the inhibition latencies will shift the peak of the inhibition recovery latencies (Fig. 5 H) from the CM by the same amount in the same direction.
At this point, the inhibition pathways are opaque to us. Examination of experimental records reveals that after the majority (>80%) of  switches from 2 to 300 µM, the channel quickly (∼30 ms) transits into a mode with low but nonzero Po, followed by a transition into a different totally quiescent mode with Po = 0. The inhibition latencies were evaluated as the durations the channel takes to enter the totally quiescent mode (Mak et al., 2007). Our present model does not distinguish the mode with low but nonzero Po from the totally quiescent mode and therefore is not equipped to properly describe this gating behavior of the channel. Incorporating this feature in the model will require future experiments to gather enough data for modeling the kinetics of these two modes. We will then be able to devise a model distinguishing the two behaviors (with at least four gating modes) to more properly account for Ca2+ inhibition kinetics of the channel.
switches from 2 to 300 µM, the channel quickly (∼30 ms) transits into a mode with low but nonzero Po, followed by a transition into a different totally quiescent mode with Po = 0. The inhibition latencies were evaluated as the durations the channel takes to enter the totally quiescent mode (Mak et al., 2007). Our present model does not distinguish the mode with low but nonzero Po from the totally quiescent mode and therefore is not equipped to properly describe this gating behavior of the channel. Incorporating this feature in the model will require future experiments to gather enough data for modeling the kinetics of these two modes. We will then be able to devise a model distinguishing the two behaviors (with at least four gating modes) to more properly account for Ca2+ inhibition kinetics of the channel.
Channel gating kinetics from the model
The mean open- and closed-channel durations (τo and τc) were calculated for various  in
in  = 10 µM (supplemental text, section 1.8). The values from the model agree reasonably well with experimental measurements over a broad range of
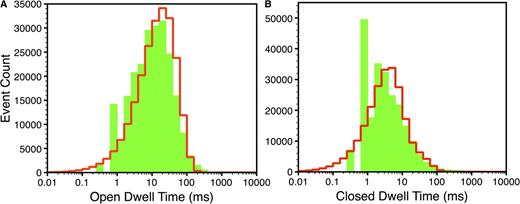
= 10 µM (supplemental text, section 1.8). The values from the model agree reasonably well with experimental measurements over a broad range of  (300 nM to 100 µM) (Fig. 6, A and B). The parameters were also used to generate simulated single-channel gating record exhibiting modal gating behavior that resembles experimental single IP3R channel current record in 1 µM Ca2+ and 10 µM IP3 (Fig. 3 B). The open and closed dwell-time distributions from the model are computed as in the supplemental text, section 1.9, and are shown by red lines in Fig. 7. The distributions obtained from the observed time-series data are shown by the green bars in Fig. 7.
(300 nM to 100 µM) (Fig. 6, A and B). The parameters were also used to generate simulated single-channel gating record exhibiting modal gating behavior that resembles experimental single IP3R channel current record in 1 µM Ca2+ and 10 µM IP3 (Fig. 3 B). The open and closed dwell-time distributions from the model are computed as in the supplemental text, section 1.9, and are shown by red lines in Fig. 7. The distributions obtained from the observed time-series data are shown by the green bars in Fig. 7.
Ca2+ dependence of IP3R channel mean open and closed times. Mean open (A) and closed times (B) for fixed  = 10 µM. The solid curves are theoretical fits, and squares are experimental values. The experimental data are taken from Ionescu et al. (2006) (supplemental text, section 1.10.1).
= 10 µM. The solid curves are theoretical fits, and squares are experimental values. The experimental data are taken from Ionescu et al. (2006) (supplemental text, section 1.10.1).
Ca2+ dependence of IP3R channel mean open and closed times. Mean open (A) and closed times (B) for fixed  = 10 µM. The solid curves are theoretical fits, and squares are experimental values. The experimental data are taken from Ionescu et al. (2006) (supplemental text, section 1.10.1).
= 10 µM. The solid curves are theoretical fits, and squares are experimental values. The experimental data are taken from Ionescu et al. (2006) (supplemental text, section 1.10.1).
Open (A) and closed (B) dwell-time distributions at  = 1 µM and
= 1 µM and  = 10 µM. Green bars are the experimental values, and red lines are the model fits.
= 10 µM. Green bars are the experimental values, and red lines are the model fits.
Open (A) and closed (B) dwell-time distributions at  = 1 µM and
= 1 µM and  = 10 µM. Green bars are the experimental values, and red lines are the model fits.
= 10 µM. Green bars are the experimental values, and red lines are the model fits.
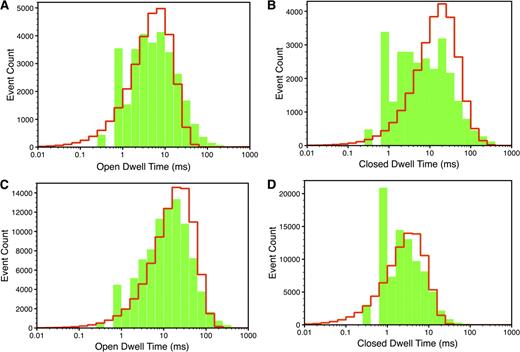
The supplemental text, section 1.9, also describes the derivation of the open and closed dwell-time distributions in H and I modes from the model. The dwell-time distributions from the model for  = 1 µM in the I and H modes are given by the red lines in Fig. 8. The experimental data are presented by the green bars for comparison. The peaks near 1 ms in the observed closed-time distributions indicate that there are short-lived closed states available to both I and H modes (Fig. 8, B and D, respectively) that the model misses. There also seems to be a short-lived open state available to the I model (Fig. 8 A). Removing this discrepancy will require adding more states to the model. At this stage, we are not interested in complicating the model further. Nevertheless, our analysis about open and closed dwell-time distributions provides useful insight into the modal behavior of the channel. The discrepancy between the model and the observed dwell-time distributions in the I mode can also be removed by increasing the flux parameter involved in transition (). However, increasing worsens the overall fit to the latency plus time-series data and therefore is not warranted.
= 1 µM in the I and H modes are given by the red lines in Fig. 8. The experimental data are presented by the green bars for comparison. The peaks near 1 ms in the observed closed-time distributions indicate that there are short-lived closed states available to both I and H modes (Fig. 8, B and D, respectively) that the model misses. There also seems to be a short-lived open state available to the I model (Fig. 8 A). Removing this discrepancy will require adding more states to the model. At this stage, we are not interested in complicating the model further. Nevertheless, our analysis about open and closed dwell-time distributions provides useful insight into the modal behavior of the channel. The discrepancy between the model and the observed dwell-time distributions in the I mode can also be removed by increasing the flux parameter involved in transition (). However, increasing worsens the overall fit to the latency plus time-series data and therefore is not warranted.
Dwell-time distributions in I and H modes at  = 1 µM and
= 1 µM and  = 10 µM. Open (A) and closed dwell-time distributions (B) in I mode. Open (C) and closed dwell-time distributions (D) in H mode. Green bars are the experimental values, and red lines are the model fits.
= 10 µM. Open (A) and closed dwell-time distributions (B) in I mode. Open (C) and closed dwell-time distributions (D) in H mode. Green bars are the experimental values, and red lines are the model fits.
Dwell-time distributions in I and H modes at  = 1 µM and
= 1 µM and  = 10 µM. Open (A) and closed dwell-time distributions (B) in I mode. Open (C) and closed dwell-time distributions (D) in H mode. Green bars are the experimental values, and red lines are the model fits.
= 10 µM. Open (A) and closed dwell-time distributions (B) in I mode. Open (C) and closed dwell-time distributions (D) in H mode. Green bars are the experimental values, and red lines are the model fits.
Comparison between the CM and the DYKM
The one model of note that gave a better AIC score for Po data only is the DYKM. Here, we compare the maximum likelihood fit of the CM (Fig. 1) to the DYKM using time-series and latency data. We find that the CM has a higher likelihood of producing the observations than does the DYKM. The DYKM has only a single open state and cannot produce modal gating, so we do not try to extract modal statistics from it.
The DYKM is a 120-state model of the IP3R. The DYKM treats the channel as consisting of three rather than four identical subunits. It assumes that the subunits are independent and that each subunit has three binding sites, one for IP3, a Ca2+ activation, and Ca2+ inhibition. The subunit states can be labeled by three binary digits (000, 001, … 111), with the first, second, and third bits representing the occupancy of the IP3, Ca2+ activation, and Ca2+ inhibition binding sites, respectively. The channel is open if all three subunits are in the (110) state and closed otherwise. The channel open probability can be written , where  with
with

where the Kmno are the occupancy parameters for the subunit states. The full-channel model has 120 states of which 119 are closed. The DYKM requires 7 occupancy and 12 flux parameters, or, equivalently, 12 independent reaction rates.
The DYKM had an AIC score ∼10 better than the CM for the Sf9 Po data. However, in the case of Xenopus Po data, the DYKM had an AIC score of −92 as compared with −138 (better) for the CM. Furthermore, we show that Po alone is inadequate to discriminate between models. To shed further light on the differences between the CM and the DYKM, we performed maximum likelihood fits on the latency data and current traces of channel gating using DYKM as described in Maximum likelihood and AIC calculations in Materials and methods. We varied the 12 free rate constants of the DYKM while holding the occupancy parameters fixed. The likelihood ratio for CM and DYKM, which is interpreted as the relative probabilities of the two models, is the exponential of the difference between their AIC scores: , where
For the DYKM, we took advantage of the fact that there is only a single open state, thus Eq. 3 becomes:
In the case of DYKM, NC = 119 and NO = 1. Thus, wO is a scalar from which it follows that . Thus, QCC is a 119 × 119 matrix, QOO is scalar (equal to minus the inverse lifetime of the single open state), and QCO and QOC are 119 × 1 and 1 × 119 matrices, respectively.
In both cases, fit to the latency data alone and fit to both the latency and time-series data (see Maximum likelihood and AIC calculations in Materials and methods), we calculated the likelihood score of the time-series data. In the first case, in which the time-series data were not used in the fit, the time-series data can be considered as “out-of-sample” data, with the differences in scores indicating which model does the best job of “predicting” the unseen data.
The results are summarized in Table 1, which demonstrate that there is strong statistical evidence for the CM. Adding more time-series data (up to 28 experiments for  = 0.1, 1, and 89 µM each) further increases the probability for the CM as compared with DYKM.
= 0.1, 1, and 89 µM each) further increases the probability for the CM as compared with DYKM.
Summary of the fits of the CM and the DYKM to data
| Model | CM | DYKM | δAIC | ExpδAIC/2 | ||||
| Exp. | LAT | LAT+TS | LAT | LAT+TS | LAT | LAT+TS | LAT | LAT+TS |
| LAT | 18213 | 18295 | 18632 | 21867 | 820 | 7126 | 10178 | 101547 |
| TS | 33327 | 32570 | 69784 | 44610 | 72896 | 24062 | 1015029 | 105225 |
| Total | 51540 | 50865 | 88416 | 66478 | 73734 | 31206 | 1016011 | 106776 |
| Model | CM | DYKM | δAIC | ExpδAIC/2 | ||||
| Exp. | LAT | LAT+TS | LAT | LAT+TS | LAT | LAT+TS | LAT | LAT+TS |
| LAT | 18213 | 18295 | 18632 | 21867 | 820 | 7126 | 10178 | 101547 |
| TS | 33327 | 32570 | 69784 | 44610 | 72896 | 24062 | 1015029 | 105225 |
| Total | 51540 | 50865 | 88416 | 66478 | 73734 | 31206 | 1016011 | 106776 |
The first column denotes the experiment class (LAT, latency; TS, time series). The columns LAT and LAT+TS, respectively, indicate that the latency data only and latency plus time-series data were used in the fit. The values in the CM and DYKM columns contain -log(likelihood(data)) scores of the CM and the DYKM, respectively, for the data given in that row. The column δAIC contains the difference in the AIC scores for the two models, with positive values indicating that the CM had the lowest (best) AIC score. The last column gives expδAIC/2 where values >1 indicate that the CM is more probable than the DYKM for that data. The row Total contains the total -log(likelihood(data)) (for columns CM and DYKM), δAIC, and expδAIC/2 scores for the latency and time-series data.
The occupancy parameters for the DYKM are given in Table S4. The rate constants are given in Table S5. The fits to the latency distributions are shown in Fig. 9.
Fits from the DYKM. Logarithmically binned latency histograms of IP3R channels responding to changes in  and
and  . In each case, (
. In each case, ( ,
,  ) are changed as indicated in Fig. 5. (A) IP3 activation, (B) IP3 deactivation, (C) Ca2+ activation, (D) Ca2+ deactivation, (E) Ca2+ and IP3 activation, (F) Ca2+ and IP3 deactivation, (G) Ca2+ inhibition, and (H) Ca2+ inhibition recovery. The experimental latency distributions given by the bars are taken from Mak et al. (2007). The red and pink lines, respectively, are from the DYKM when fit to the latency data alone and latency and times-series data simultaneously. The black line is from the CM developed in this paper when fit to the latency and times-series data simultaneously and is shown for comparison.
) are changed as indicated in Fig. 5. (A) IP3 activation, (B) IP3 deactivation, (C) Ca2+ activation, (D) Ca2+ deactivation, (E) Ca2+ and IP3 activation, (F) Ca2+ and IP3 deactivation, (G) Ca2+ inhibition, and (H) Ca2+ inhibition recovery. The experimental latency distributions given by the bars are taken from Mak et al. (2007). The red and pink lines, respectively, are from the DYKM when fit to the latency data alone and latency and times-series data simultaneously. The black line is from the CM developed in this paper when fit to the latency and times-series data simultaneously and is shown for comparison.
Fits from the DYKM. Logarithmically binned latency histograms of IP3R channels responding to changes in  and
and  . In each case, (
. In each case, ( ,
,  ) are changed as indicated in Fig. 5. (A) IP3 activation, (B) IP3 deactivation, (C) Ca2+ activation, (D) Ca2+ deactivation, (E) Ca2+ and IP3 activation, (F) Ca2+ and IP3 deactivation, (G) Ca2+ inhibition, and (H) Ca2+ inhibition recovery. The experimental latency distributions given by the bars are taken from Mak et al. (2007). The red and pink lines, respectively, are from the DYKM when fit to the latency data alone and latency and times-series data simultaneously. The black line is from the CM developed in this paper when fit to the latency and times-series data simultaneously and is shown for comparison.
) are changed as indicated in Fig. 5. (A) IP3 activation, (B) IP3 deactivation, (C) Ca2+ activation, (D) Ca2+ deactivation, (E) Ca2+ and IP3 activation, (F) Ca2+ and IP3 deactivation, (G) Ca2+ inhibition, and (H) Ca2+ inhibition recovery. The experimental latency distributions given by the bars are taken from Mak et al. (2007). The red and pink lines, respectively, are from the DYKM when fit to the latency data alone and latency and times-series data simultaneously. The black line is from the CM developed in this paper when fit to the latency and times-series data simultaneously and is shown for comparison.
DISCUSSION
Deficiencies of the CM
In a famously titled section heading, George Box wrote “All models are wrong …” (Box, 1979). Ours is no exception. One of the major deficiencies of the CM is its lack of distinction between the gating mode in which the IP3R channel gates with low (∼0.05) but nonzero Po and the mode in which the channel is quiescent with Po = 0 (Q mode). In the study of IP3R modal gating behaviors under steady-state ligand conditions (Ionescu et al., 2007), it is difficult to tell if a channel remains closed for a long duration whether it stays in the L mode during that whole duration or has spontaneously entered into and exited from the Q mode during that time. However, reexamination of Ca2+ inhibition latency measurements reveals that the distinction between the L and Q mode is significant because the majority of such inhibition events proceed from channel in H mode, favored by the initial ligand conditions of ( ,
,  ) = (2 µM, 10 µM), through the L mode to the Q mode, instead of going directly from the H mode into the Q mode. Thus, the latencies consist of two contributions: the time for the channel to transit from the H mode to the L mode and the time for the channel to enter the Q mode from the L mode.
) = (2 µM, 10 µM), through the L mode to the Q mode, instead of going directly from the H mode into the Q mode. Thus, the latencies consist of two contributions: the time for the channel to transit from the H mode to the L mode and the time for the channel to enter the Q mode from the L mode.
Furthermore, the Ca2+ inhibition latency distribution clearly shows two peaks (at ∼70 and 900 ms). A natural explanation for this derived from the CM is that the short latencies are caused by channel transiting directly from to , whereas the long latencies are a result of the channels initially in I mode that have to transit into the H mode, which takes a long time because of the long τI, before they can be inhibited. However, examination of data records indicates that channel initially in the I mode when  is changed enters the L mode very rapidly (∼3 ms). Thus, the long Ca2+ inhibition latencies are caused by the slow exit from the L mode into the Q mode. To properly model Ca2+ inhibition of IP3R requires distinguishing the L mode from Q mode by including open OL states for the channel in the L mode, which will increase the complexity of the model substantially. We believe that a more accurate description of the inhibition latencies is crucial for the understanding of how the channel functions and will be the subject of our future research.
is changed enters the L mode very rapidly (∼3 ms). Thus, the long Ca2+ inhibition latencies are caused by the slow exit from the L mode into the Q mode. To properly model Ca2+ inhibition of IP3R requires distinguishing the L mode from Q mode by including open OL states for the channel in the L mode, which will increase the complexity of the model substantially. We believe that a more accurate description of the inhibition latencies is crucial for the understanding of how the channel functions and will be the subject of our future research.
The CM has a slightly higher number of short IP3 activation latencies (<10 ms) compared with the latency data. This may be a consequence of the exclusion of low occupancy states during IP3 binding (like the Ci1, Ci2, and Ci3 states excluded from the connection) applied to simplify our model. However, if this is true, it suggests that the channel binds IP3 at a rate of ∼0.4 ms−1, substantially slower than the diffusion-limited rate of ∼20 ms−1 in  = 10 µM (assuming a reaction radius of 1 nm and diffusion coefficient of 0.5 µm2 ms−1 for IP3; Redner, 2001). This indicates that IP3 probably needs to enter its binding site in IP3R with a particular orientation, as suggested by the structure of the site in the receptor with residues from different parts of the site interacting with different phosphate groups in IP3 through networks of hydrogen bonds (Bosanac et al., 2002). Alternately, this may be caused by slow conformation changes the channel has to undergo after each IP3 binding that prolongs the activation latencies.
= 10 µM (assuming a reaction radius of 1 nm and diffusion coefficient of 0.5 µm2 ms−1 for IP3; Redner, 2001). This indicates that IP3 probably needs to enter its binding site in IP3R with a particular orientation, as suggested by the structure of the site in the receptor with residues from different parts of the site interacting with different phosphate groups in IP3 through networks of hydrogen bonds (Bosanac et al., 2002). Alternately, this may be caused by slow conformation changes the channel has to undergo after each IP3 binding that prolongs the activation latencies.
With activation and deactivation latencies considered only for  jumping between <10 nM and 2 µM and
jumping between <10 nM and 2 µM and  between 0 and 10 µM, there are insufficient data about the dynamic behaviors of the IP3R channel with one to three IP3 or only one Ca2+ bound for the CM to include those states explicitly under the simplicity principle. The failure of the model to generate two resolved peaks for the Ca2+ deactivation latency distribution (Fig. 5 D) suggests that those processes probably involve multiple fast transitions through intermediate states, particularly for Ca2+ activation. Future latency measurements involving
between 0 and 10 µM, there are insufficient data about the dynamic behaviors of the IP3R channel with one to three IP3 or only one Ca2+ bound for the CM to include those states explicitly under the simplicity principle. The failure of the model to generate two resolved peaks for the Ca2+ deactivation latency distribution (Fig. 5 D) suggests that those processes probably involve multiple fast transitions through intermediate states, particularly for Ca2+ activation. Future latency measurements involving  jumping between 0 and subsaturating levels (100 nM, say) and/or
jumping between 0 and subsaturating levels (100 nM, say) and/or  between <10 nM and suboptimal levels (300 nM, say) could provide more insights into these processes to improve the model. Finally, we cannot rule out the possibility of other simple models that might better describe our data.
between <10 nM and suboptimal levels (300 nM, say) could provide more insights into these processes to improve the model. Finally, we cannot rule out the possibility of other simple models that might better describe our data.
Strengths of the CM
The rest of Box’s section heading was “… some models are useful.” The CM is the result of the synthesis of a large body of data gathered in several studies of many different aspects of ligand regulations of IP3R channel gating in a novel, data-driven minimalist approach. The model uses five to six complex occupancy parameters to capture accurately not only the Ca2+ but also the IP3 dependencies of the channel equilibrium Po. The model does a fair job of accounting for the Po, τo, τc, modal gating statistics, and the majority of latency distributions examined. Moreover, our model makes concrete predictions regarding the single-channel response to rapid changes in the cytosolic ligand concentrations of IP3 and Ca2+, so its validity can be verified by future experiments. With jumps of ( ,
,  ) from (2 µM, 0) to (2 µM, 10 µM), the channel mostly enters the H mode from . However, in lower
) from (2 µM, 0) to (2 µM, 10 µM), the channel mostly enters the H mode from . However, in lower  , the initial occupancy of will be higher so jump in
, the initial occupancy of will be higher so jump in  will activate the channel more frequently from , and then through a Ca2+-dependent transition to either or . The latency will increase with decreasing
will activate the channel more frequently from , and then through a Ca2+-dependent transition to either or . The latency will increase with decreasing  because of the Ca2+-dependent step. In high
because of the Ca2+-dependent step. In high  , the probability of the channel being activated from will increase with
, the probability of the channel being activated from will increase with  . Because the pathways out of are both slow, the IP3 activation latency should increase with increase in
. Because the pathways out of are both slow, the IP3 activation latency should increase with increase in  . Thus, our model predicts that the mean IP3 activation latency has a minimum of ≈0.26 s at moderate
. Thus, our model predicts that the mean IP3 activation latency has a minimum of ≈0.26 s at moderate  of ∼0.6 µM (Fig. S5).
of ∼0.6 µM (Fig. S5).
The CM predicts that a higher number of longer Ca2+ activation latencies will be detected if the channel is exposed to  < 10 nM longer than the 2 s used (Mak et al., 2007) before
< 10 nM longer than the 2 s used (Mak et al., 2007) before  is changed to 2 µM. This is because the relatively Ca2+-independent τI (∼0.4 s) observed suggests that the channel may not be fully equilibrated between the and states during the time the channel remains exposed to
is changed to 2 µM. This is because the relatively Ca2+-independent τI (∼0.4 s) observed suggests that the channel may not be fully equilibrated between the and states during the time the channel remains exposed to  < 10 nM. Longer exposure will increase the occupancy of , from which the channel will take longer to exit, thus giving longer Ca2+ activation latencies.
< 10 nM. Longer exposure will increase the occupancy of , from which the channel will take longer to exit, thus giving longer Ca2+ activation latencies.
As mentioned in Maximum likelihood and AIC calculations in Materials and methods, we minimize the number of parameters by assuming that the effective rates for the reactions from the states with no Ca2+ bound to the states with two Ca2+ bound are the same at  = 0, 10 µM. Relaxing this constraint did not improve the fit to the data. This result indicates that the transition rate from the states with no Ca2+ bound to the states with two Ca2+ bound is independent of the number of IP3 bound. Whether this assertion is correct or not can be investigated further by performing more ligand jump experiments, where
= 0, 10 µM. Relaxing this constraint did not improve the fit to the data. This result indicates that the transition rate from the states with no Ca2+ bound to the states with two Ca2+ bound is independent of the number of IP3 bound. Whether this assertion is correct or not can be investigated further by performing more ligand jump experiments, where  is jumped from 0 µM to suboptimal values, e.g., jumping (
is jumped from 0 µM to suboptimal values, e.g., jumping ( ,
,  ) from (0 µM , 0 µM) to (0.5 µM , 0 µM) and (0 µM , 10 µM) to (0.5 µM , 10 µM).
) from (0 µM , 0 µM) to (0.5 µM , 0 µM) and (0 µM , 10 µM) to (0.5 µM , 10 µM).
The CM, especially its deficiencies, provides novel insights that are not immediately obvious from available data. The failure of the CM to adequately account for the Ca2+ inhibition latency distribution reveals the importance of drawing the distinction between the L mode with low but nonzero Po and the quiescent Q mode with Po = 0 for improving our understanding of Ca2+ regulation of the channel, which is not obvious from the modal analysis in Ionescu et al. (2007).
Although the development of the CM is directed by experimental observations, it also provides insights to guide the designs of future experiments and data analysis protocols. Our model suggests that experiments in which  is switched between 0 and subsaturating levels and
is switched between 0 and subsaturating levels and  between physiological resting to suboptimal levels can provide valuable information to improve the characterization of the kinetics of the channel with one to three IP3 bound, and channels with one Ca2+ bound. The model also reveals that the amount of time required for the channel to fully equilibrate in one combination of (
between physiological resting to suboptimal levels can provide valuable information to improve the characterization of the kinetics of the channel with one to three IP3 bound, and channels with one Ca2+ bound. The model also reveals that the amount of time required for the channel to fully equilibrate in one combination of ( ,
,  ) before the ligand conditions can be changed in latency measurements, and that varying the time the channel stays in one ligand combination before perfusion solution switches can provide valuable information on kinetic rates. Furthermore, analysis of Ca2+ inhibition latencies should include measuring the duration between the time when
) before the ligand conditions can be changed in latency measurements, and that varying the time the channel stays in one ligand combination before perfusion solution switches can provide valuable information on kinetic rates. Furthermore, analysis of Ca2+ inhibition latencies should include measuring the duration between the time when  is changed and the time when the channel enters the L mode, and the duration when the channel stays in the L mode until its activity terminates as it enters the Q mode. We suspect that there are significant surprises in store regarding the mechanistic interpretation of inhibition.
is changed and the time when the channel enters the L mode, and the duration when the channel stays in the L mode until its activity terminates as it enters the Q mode. We suspect that there are significant surprises in store regarding the mechanistic interpretation of inhibition.
Although the aim here was to model the IP3R Ca2+ channel, our methods can be easily applied to other channels and single-molecule dynamics.
Acknowledgments
We would like to acknowledge the resources and support provided by J. Kevin Foskett and many useful conversations with Bill Bruno, Andy Fraser, Nick Hengartner, Ben McMahon, Paul Fenimore, Hans Frauenfelder, Joel Berenzden, Peter Hraber, Ian Parker, Jian-Wei Shuai, Silvina Ponce Dawson, Tony Auerbach, David Colquhoun, Fred Sachs, and Horia Vais.
This work was supported by National Institutes of Health (grant 5RO1GM065830-08).
Sharona E. Gordon served as editor.